NeurIPS 2023 | 如何从理论上研究生成式数据增强的效果？

最新推荐文章于 2025-01-12 19:43:38 发布

PaperWeekly

最新推荐文章于 2025-01-12 19:43:38 发布

阅读量329

点赞数

原文链接：https://mp.weixin.qq.com/s?__biz=MzIwMTc4ODE0Mw==&mid=2247639696&idx=3&sn=df1c549a23fe9099b303d0b79b2151da&chksm=96e47d10a193f40688356e2cb45cd307eee79c5380ed17729d3ee33d6696b78ce7df75369a78&scene=126&sessionid=0

版权

©作者 | 郑晨宇

学校 | 中国人民大学

研究方向 | 机器学习理论

论文链接：

https://arxiv.org/abs/2305.17476

代码链接：

https://github.com/ML-GSAI/Understanding-GDA

概述

生成式数据扩增通过条件生成模型生成新样本来扩展数据集，从而提高各种学习任务的分类性能。然而，很少有人从理论上研究生成数据增强的效果。为了填补这一空白，我们在这种非独立同分布环境下构建了基于稳定性的通用泛化误差界。基于通用的泛化界，我们进一步了探究了高斯混合模型和生成对抗网络的学习情况。

在这两种情况下，我们证明了，虽然生成式数据增强并不能享受更快的学习率，但当训练集较小时，它可以在一个常数的水平上提高学习保证，这在发生过拟合时是非常重要的。最后，高斯混合模型的仿真结果和生成式对抗网络的实验结果都支持我们的理论结论。

主要的理论结果

2.1 符号与定义

让作为数据输入空间，作为标签空间。定义为上的真实分布。给定集合，我们定义为去掉第个数据后剩下的集合，为把第个数据换成后的集合。我们用表示 total variation distance。

我们让为所有从到的所有可测函数，为学习算法，为从数据集中学到的映射。对于一个学到的映射和损失函数，真实误差被定义为。相应的经验的误差被定义为。

我们文章理论推导采用的是稳定性框架，我们称算法相对于损失函数是一致稳定的，如果

2.2 生成式数据增强

给定带有个 i.i.d. 样本的数据集，我们能训练一个条件生成模型，并将学到的分布定义为。基于训练得到的条件生成模型，我们能生成一个新的具有个 i.i.d. 样本的数据集。我们记增广后的数据集大小为。我们可以在增广后的数据集上学到映射。为了理解生成式数据增强，我们关心泛化误差。据我们所知，这是第一个理解生成式数据增强泛化误差的工作。

2.3 一般情况

我们可以对于任意的生成器和一致稳定的分类器，推得如下的泛化误差：

▲ general

一般来说，我们比较关心泛化误差界关于样本数的收敛率。将看成超参数，并将后面两项记为 generalization error w.r.t. mixed distribution，我们可以定义如下的“最有效的增强数量”：

在这个设置下，并和没有数据增强的情况进行对比（），我们可以得到如下的充分条件，它刻画了生成式数据增强何时（不）能够促进下游分类任务，这和生成模型学习分的能力息息相关：

▲ corollary

2.4 高斯混合模型

为了验证我们理论的正确性，我们先考虑了一个简单的高斯混合模型的 setting。

混合高斯分布。我们考虑二分类任务。我们假设真实分布满足 and 。我们假设的分布是已知的。

线性分类器。我们考虑一个被参数化的分类器，预测函数为。给定训练集，通过最小化负对数似然损失函数得到，即最小化

学习算法将会推得，which satisfies

条件生成模型。我们考虑参数为的条件生成模型，其中以及。给定训练集，让为第类的样本量，条件生成模型学到

它们是和的无偏估计。我们可以从这个条件模型中进行采样，即，，其中。

我们在高斯混合模型的场景下具体计算 Theorem 3.1 中的各个项，可以推得

▲ GMM

当数据量足够时，即使我们采用“最有效的增强数量”，生成式数据增强也难以提高下游任务的分类性能。
当数据量较小的，此时主导泛化误差的是维度等其他项，此时进行生成式数据增强可以常数级降低泛化误差，这意味着在过拟合的场景下，生成式数据增强是很有必要的。

2.5 生成对抗网络

我们也考虑了深度学习的情况。我们假设生成模型为 MLP 生成对抗网络，分类器为层 MLP 或者 CNN。损失函数为二元交叉熵，优化算法为 SGD。我们假设损失函数平滑，并且第层的神经网络参数可以被控制。我们可以推得如下的结论：

▲ GAN

当数据量足够时，生成式数据增强也难以提高下游任务的分类性能，甚至会恶化。
当数据量较小的，此时主导泛化误差的是维度等其他项，此时进行生成式数据增强可以常数级降低泛化误差，同样地，这意味着在过拟合的场景下，生成式数据增强是很有必要的。

实验

3.1 高斯混合模型模拟实验

我们在混合高斯分布上验证我们的理论，我们调整数据量，数据维度以及。实验结果如下图所示：

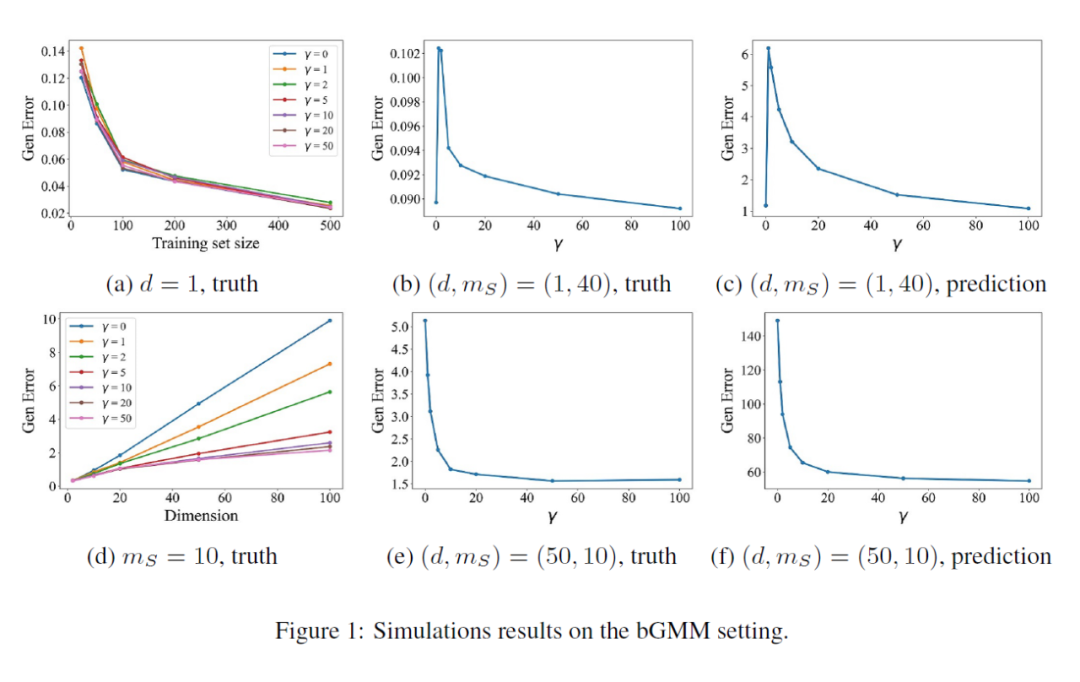
▲ simulation

观察图（a），我们可以发现当相对于足够大的时候，生成式数据增强的引入并不能明显改变泛化误差。
观察图（d），我们可以发现当固定时，真实的泛化误差确实是阶的，且随着增强数量的增大，泛化误差呈现常数级的降低。
另外 4 张图，我们选取了两种情况，验证了我们的 bound 能在趋势上一定程度上预测泛化误差。

这些结果支持了我们理论的正确性。

3.2 深度生成模型实验

我们使用 ResNet 作为分类器，cDCGAN、StyleGANv2-ADA 和 EDM 作为深度生成模型，在 CIFAR-10 数据集上进行了实验。实验结果如下所示。由于训练集上训练误差都接近 0，所以测试集上的错误率是泛化误差的一个比较好的估计。我们利用是否做额外的数据增强（翻转等）来近似是否充足。

▲ deep

在没有额外数据增强的时候，较小，分类器陷入了严重的过拟合。此时，即使选取的 cDCGAN 很古早（bad GAN），生成式数据增强都能带来明显的提升。
在有额外数据增强的时候，充足。此时，即使选取的 StyleGAN 很先进（SOTA GAN），生成式数据增强都难以带来明显的提升，在 50k 和 100k 增强的情况下甚至都造成了一致的损害。
我们也测试了一个 SOTA 的扩散模型 EDM，发现即使在有额外数据增强的时候，生成式数据增强也能提升分类效果。这意味着扩散模型学习分布的能力可能会优于 GAN。

更多阅读