LLM领域首次实现量化推理自由！字节开源ABQ-LLM，效果和性能双SOTA-CSDN博客

©PaperWeekly 原创 · 作者 | 刘松伟

单位 | 字节跳动

研究方向 | 大模型推理/模型优化，MLsys

文章地址：

https://arxiv.org/abs/2408.08554

项目地址：

https://github.com/bytedance/ABQ-LLM

作者单位：

字节跳动-智能创作-ByteNN

ABQ-LLM 是面向 AIGC 领域的算法系统协同优化工作，旨在解决 LLM 量化中存在的两大主要挑战：

1. 低位量化致使的效果严重降低；

2. 主流 GPU 对整数矩阵乘支持有限所引发的计算效率低下问题。

在推理引擎层面，我们基于二值化矩阵乘（BTC）等价重构了任意精度组合的矩阵乘，从而突破了 INT4/INT8 计算单元的限制，开创性地实现了任意比特量化组合的直接加速，结合深度工程优化，实现了 decoding 阶段对 cutlass/cublas 加速库的大幅性能领先。

在算法方面，我们运用了基于 transformer block 的分布纠正和低比特位平衡策略，有效提升低位量化效果。我们在各类量化配置下均达成了 SOTA 的效果，综合模型效果优于 OmniQuant、AffineQuant 等前期工作，同时工程实现大幅超越 SmoothQuant，端到端综合性能超越 SmoothQuant 实现了 1.6 的推理加速和 2.7 的内存压缩。

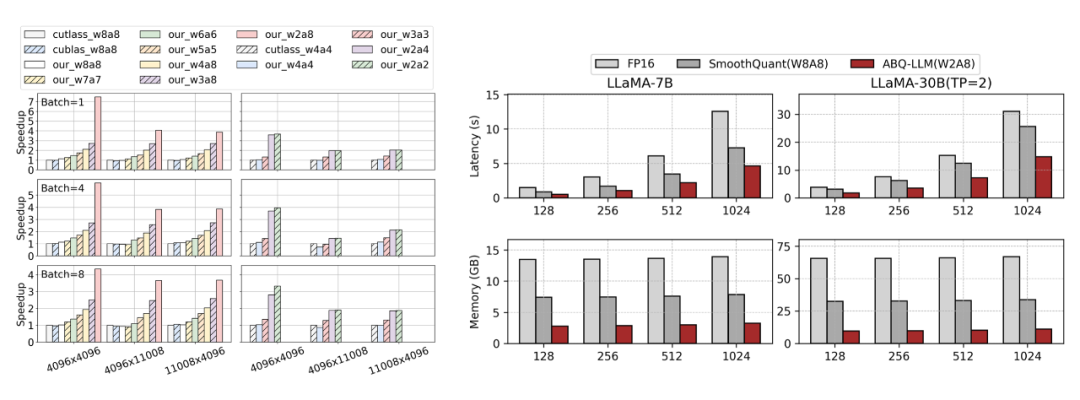
▲ 图1.（左）算子级性能对比，ABQKernel 可以有效地将位宽收益转化为加速收益，以 W2A8 为例，相比 cutlass W8A8 具备 3.8~7.48 倍的单核加速（右）端到端性能对比，在 fastertransformer 框架中，ABQ-LLM 相比业界 SOTA 的 SmoothQuant 方案实现了 1.6× 的推理加速和 2.7× 的内存压缩

Abstract

大型语言模型（LLM）为自然语言处理带来了革命性的变化，但在推理过程中却受到大量内存和计算需求的限制。PTQ 提供了一种很有前景的解决方案，但它也面临着一些挑战，例如低位量化导致的性能下降，以及主流 GPU 的整数支持有限导致的计算效率低下。

我们提出的任意位量化方案 ABQ-LLM 是一种新型的 PTQ 方法，可以解决上述问题。ABQ 支持任意位量化权重和激活，并使用二进制表示执行矩阵计算。

这种方法有两大优势：它能在不损失精度的情况下实现任意位量化矩阵计算，并绕过 INT4/INT8 单元的限制，利用二值化矩阵乘单元实现高效计算和高吞吐量。

为了解决低位宽时的性能下降问题，我们采用了两种增强技术：一种是 transformer block 的分布校正方法，用于解决权重和激活全量化过程中的分布偏移问题；另一种是位平衡策略，用于缓解超低位宽（如 2 比特）时的非对称分布问题。

实验结果表明，ABQ 在各种量化设置（包括 W2A8、W4A4 和 W6A6）下都具有出色的灵活性和具备竞争力的性能。

Introduction

大规模语言模型（LLM）对计算/带宽/内存的需求日益增长，其在实际应用场景中的部署受到了极大限制。后训练量化（PTQ）成为解决计算和带宽瓶颈的一种有效手段。然而当前业界的量化方法，无论是仅针对权重的量化（weight-only），还是权重和激活值的全量化（weight-activation），都无法突破主流 GPU 整数运算单元的限制。

在推理阶段，weight-only 量化方法仍然需要将数据反量化为 FP16 进行计算。对于 weight-activation 量化，如图 2 所示，主流推理引擎局限于 INT4/INT8 计算单元的能力，在实际计算时仍需要将 W/A 精度转换为 INT4/INT8，引入额外的反量化指令耗时，这导致 LLM 领域量化算法的探索局限在 W4A4 和 W8A8，极大地限制了算法设计空间。

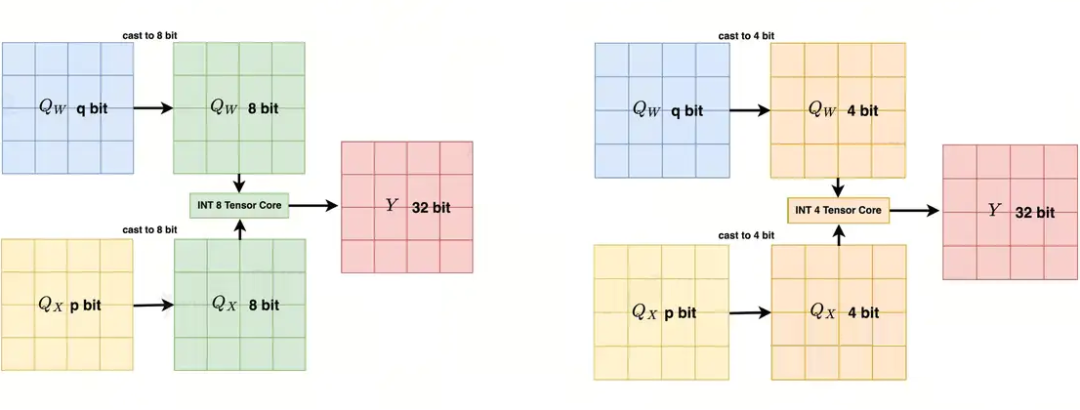
▲ 图2. 在 NVIDIA GPU 上，非 W4A4/W8A8 位宽组合需要离线或者在线反量化至 4/8Bit，以满足 INT4/8 TensorCore 的的要求

此外，现有的量化方案在低比特位精度下仍存在显著的性能劣化。例如，SoothQuant、OmniQuant、AffineQuant 等方法在 W4A4、W3A4、W2A16 和 W2A8 等低比特位设置下表现出较大的精度下降，从而影响了量化模型的实际使用体验。

为了解决上述问题，我们提出了 ABQ-LLM。根据我们所知，这是首个在大规模语言模型（LLM）中实现量化推理自由的研究工作。我们的主要贡献包括：

在 LLM 领域中首次实现了量化推理自由。我们巧妙地基于 BTC（Binary TensorCore，BTC）等效重构了任意精度组合的量化矩阵乘法，突破了 INT4/INT8 计算单元的限制，使每一位压缩的位宽收益都能够转化为实际的加速收益，并有效规避了 GEMV 问题，充分挖掘了量化模型在更多混合精度（如 W2A6、W2A8）下的综合优势。
引入了 Transformer 模块的分布纠正方法，以缓解全量化处理 weight 和 activation 时导致的分布差异，从而提升了低比特位下的模型性能。针对极低比特位（如 2 比特）下出现的非对称分布问题，采用位平衡策略，以弥补 W2 量化带来的性能损失。

Method

3.1 分布矫正策略

▎Distribution Correction

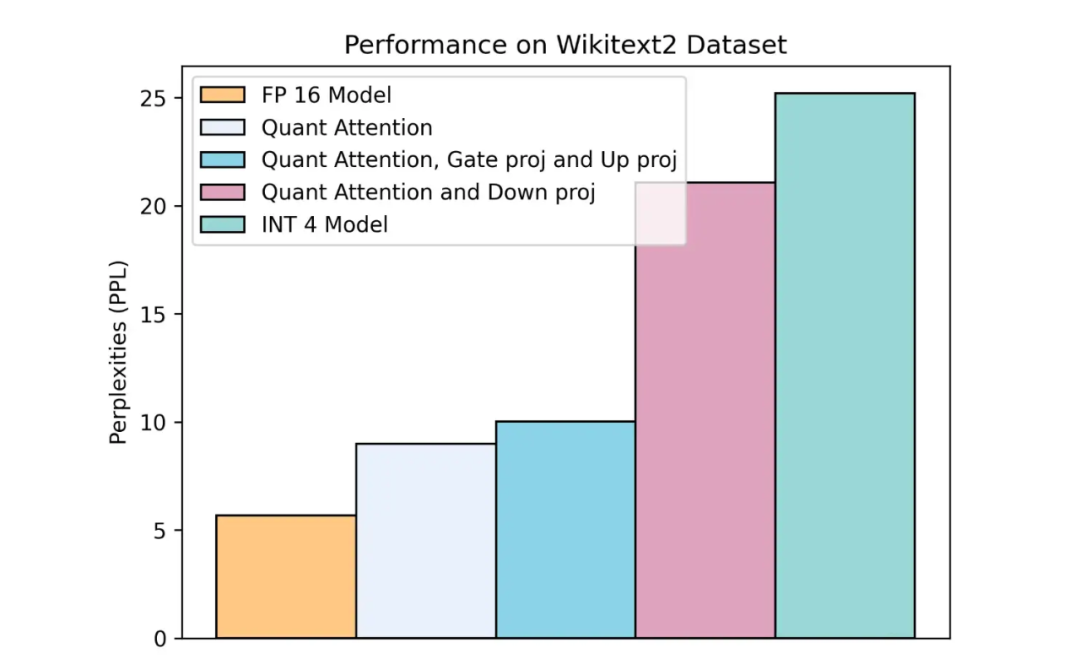
▲ 图3. LLaMA-7B transformer block 各模块量化带来的精度损失（Wikitext2 PPL 越低越好）

LLM 模型在量化时不同层的敏感性存在显著差异，某些层对 LLM 的量化性能起着决定性作用。为验证这一观点，如上图 3 所示，我们在 weight-activation 全量化场景下对 LLaMA-7B 模型 Transformer Block 中的不同组件进行了量化。

当量化 Attention 和 MLP 中的 gate_proj 层和 up_proj 层时，模型性能仅出现了轻微下降。然而，一旦对 down_proj linear 层进行量化时，模型性能出现了显著的下降，表明对 down_proj 量化的处理是性能恢复的关键难点。

我们进一步观察到，down_proj 量化导致性能下降的主要原因在于对 down_proj 激活的量化。由于在 INT4、INT3 和 INT2 等低比特位下表示范围受限，量化后模型的分布相较于全精度表示发生了显著偏移。因此，在量化校验过程中，我们对 down_proj 的输出建立了双余弦相似度损失，以纠正量化后模型 down_proj 输出的分布。具体的损失函数如下：

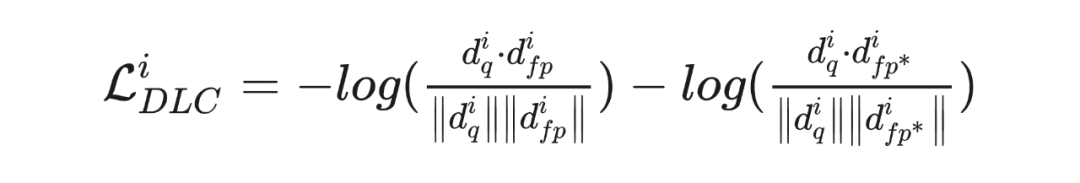
其中，代表第 i 个 Transformer Block 量化后的输出，代表第 i 个 transformer 块全精度的输出，代表第 i 个 transformer 块全精度的输出，但其输入来自第 i−1 个 transformer 块量化后的输出。

此外，我们进一步分析了 LLaMA-7B 模型中激活值经过 decoder block 后的输入和输出余弦相似度变化。观察结果表明，模型首尾几个块的激活输入和输出余弦相似度存在显著差异，这表明这些首尾块对模型推理性能有较大影响。针对这一现象，我们对首尾块的 down_proj 层施加了 vector 分布补偿，以弥补这些块之间的分布差异。

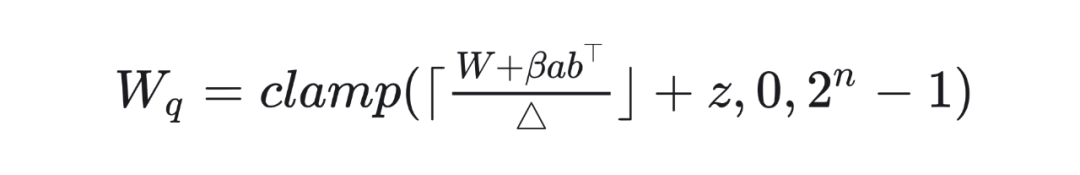
其中，代表 round-to-nearest operation，n 代表比特数，代表 step size，z 是 zero point。是量化后的权重， W 是全精度的权重，a 和 b 是分布补偿向量，b 用于控制是否进行补偿，b=1 表示进行补偿，b=0 则不进行补偿。

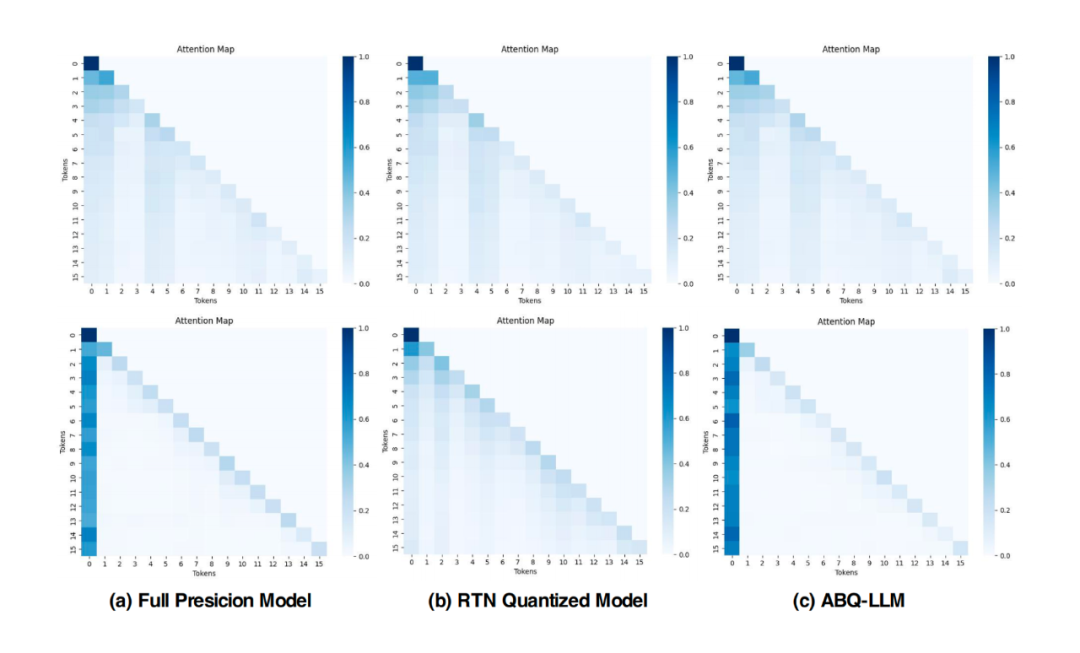
▲ 图4. 第一个 Transformer Block（上图）和最后一个 Transformer Block（下图）的注意力分布图

为了进一步提升量化模型的性能，我们研究了量化前（a）后（b）Attention Map 的分布变化，如图 4 所示，在全精度模型中，大量注意力集中在序列的首 token 上，这表明在文本生成过程中，首 token 起到了关键的引导作用，这一现象与 LLM-QAT [1] 中的结论一致。

然而，量化后模型的注意力分布显著改变，文本序列对首 token 的关注度受到了干扰。为了解决这一问题，并在量化过程中恢复模型对首 token 的关注，我们引入了 attention-aware KL 散度，以重建 attention map 注意力分布，经过 AKL 损失重建我们的 ABQ 量化后与全精度保持了相似的 Attention Map 分布。

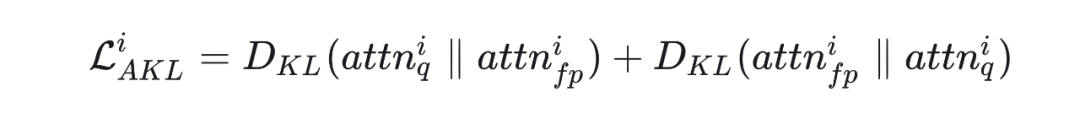
其中，代表第 i 个 Transformer Block 量化后 attention map 输出，代表第 i 个 Transformer Block 全精度的 attention map 输出。

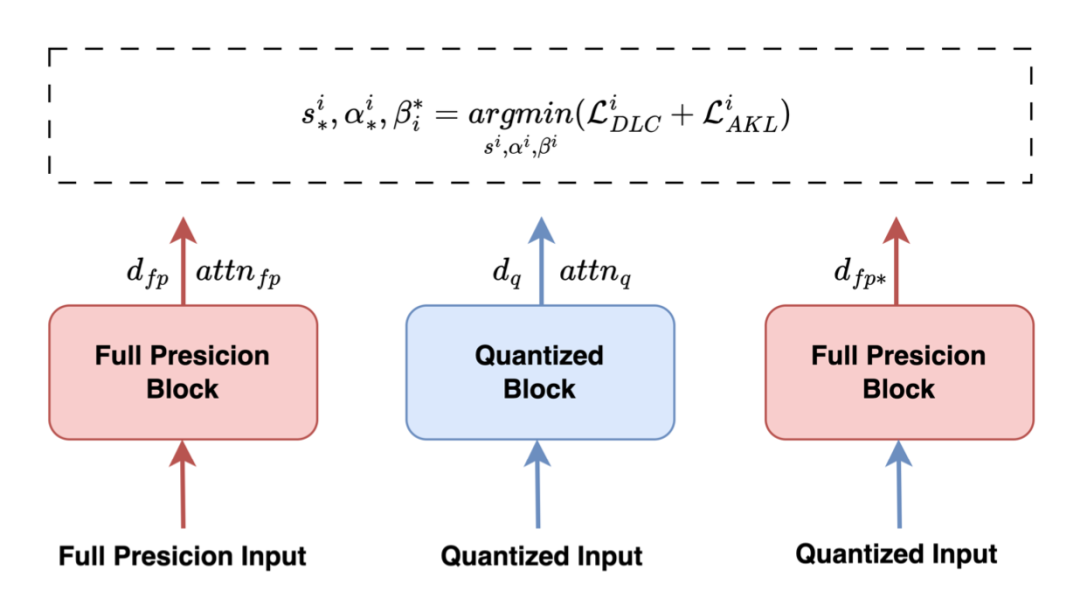
▲ 图5. ABQ-LLM 算法概述。ABQ-LLM 使用 DLC loss 和 AKL loss 来更新可学习的量化参数

最后，我们将 DLC 损失和 AKL 损失结合起来，如图 5 所示得到我们最终的优化目标如下：

其中，、和为校验完成后第 i 个 Transformer Block 的量化参数。当量化输出和全精度输出的分布相匹配时，我们的总体损失接近于 0，这将有效地指导量化过程。

3.2 位平衡策略

▎Bit Balance Strategy

预训练的 LLM 模型权重分布趋近于正态分布，具有对称性。然而，在普通的 INT2 量化配置下，数值表示范围仅包含四个值，进行对称量化时可选的表示范围为 {-2, -1, 0, 1} 或 {-1, 0, 1, 2}，这破坏了模型权重原有的对称分布属性。这种不对称性导致模型性能显著下降，从 W4A16 到 W3A16 性能下降了 0.46，而从 W3A16 到 W2A16 性能下降了 4.87，出现了大幅异常下跌。

为了解决这种不对称性对 LLM 模型量化的影响，我们借鉴了 BitNet1.58 [2] 的位平衡策略，对 INT2 量化进行了改进，将 INT2 对称量化的表示空间扩展为 {-2, -1, 0, 1, 2}。通过这一改进，模型性能恢复到 7.50，与 W3A16 性能相比，属于一个合理的变化范围。

计算等价重构

▎Reconstructing Arbitrary Bit Computation

NVIDIA 在图灵以上架构中引入了 INT1 TensorCore 用于支持业界 W1A1 量化算法的发展，由于完全基于位运算，因此其峰值算力高达 INT4/INT8 的 4/8 倍。然而，由于巨大的效果损失，1Bit 量化至今未实际落地，该硬件单元始终未得到业界充分利用。我们在数学层面对量化矩阵乘进行分析，发现任意量化组合的运算均可分解为 1-bit 的矩阵乘的特殊叠加。

假设神经网路的某一层的权重 W 被量化为 bit，输入激活值 X 被量化为 bit，W 和 X 执行矩阵乘运算得到 32 bit 的输出，关键观察是：权重 W 和激活值 X 的任意位置的标量数值都可以分解为一系列 1 bit 标量数字，任意精度组合的标量运算可以被分解为 1 bit 运算和移位操作。

形式上，为了支持标量级别的任意精度组合运算，例如 1 bit 权重和 2 bit 激活值的标量级任意精度计算，我们可以首先进行形式变换，例如 2 bit 的 x 可以被表示为

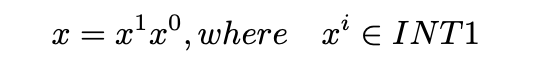
其中，我们使用来表示输入是 1bit 数据，输出是 32-bit 的计算操作，那么原来的标量级任意精度计算可以被表示为

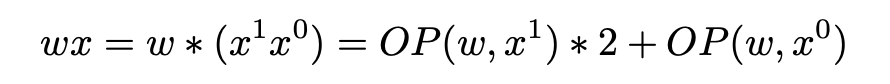
上述过程可以自然推广到具有任意位和的矩阵乘组合。形式上，给定一个位权重矩阵和一个位权重矩阵，我们可以首先分解为 1 位矩阵和。

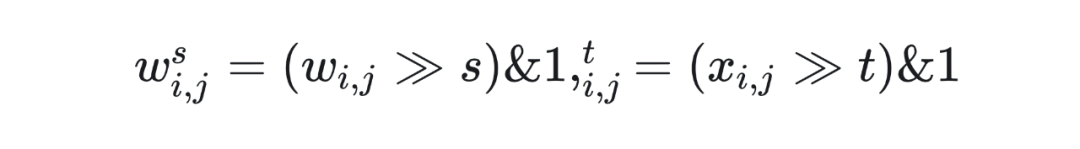
假如以 BMMA 代表 1 bit 矩阵乘运算，那么可以调用 BMMA 运算 p*q 次，计算一系列的 1-bit 矩阵乘分量

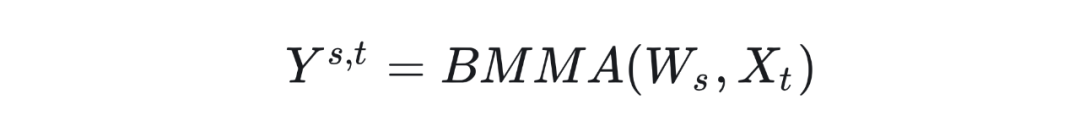
最终，我们将所有的 1-bit 矩阵乘分量进行位叠加的缩放系数处理，之后进行累加得到 32-bit 的输出矩阵

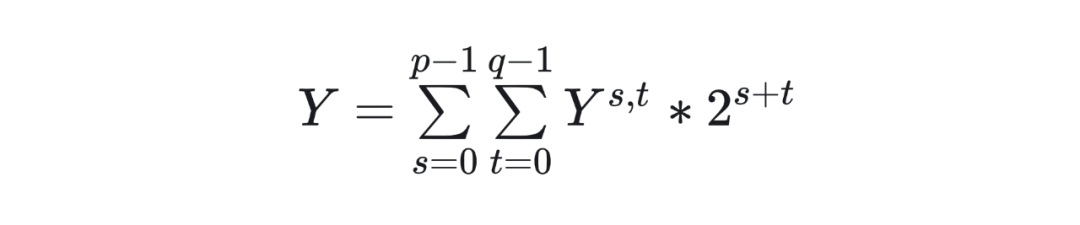
经过上述变换过程，我们将任意量化组合的运算分解为 1-bit 的矩阵乘的特殊叠加，使底层可以调用高算力的 BMMA 指令实现，主要收益如下

有效解决 GEMV 的计算效率问题，由于底层计算时真实 M 维度是 BatchSize * X_BIT，X_BIT=8 时 BatchSize 无论多大均是 8 的整数，有效提升 Decoding 阶段（BatchSize=1）的计算密度。
首次以一种统一的方式支持任意 Bit 的量化组合计算，不但可以根据模型规模合理选择不同的量化组合，同时底层实现高效。

3.3 推理引擎实现

▎Engine Implementation

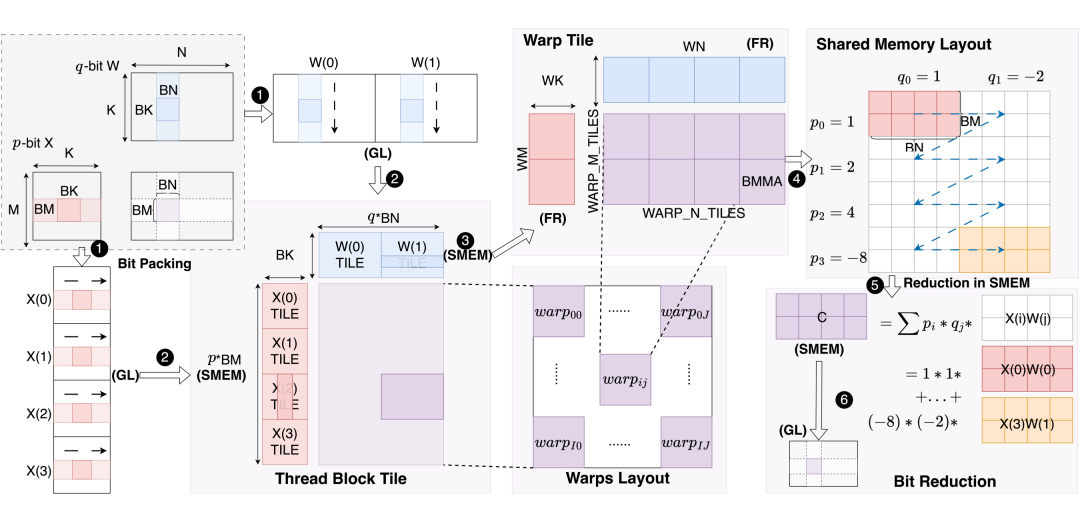
▲ 图6.（左）推理引擎计算任务拆解图. p 和 q 分别代表输入 X 和权重 W 的量化位宽，数据流动被精心设计以实现高效计算：GL 到 SMEM 到 FR 到 SMEM 到 GL.

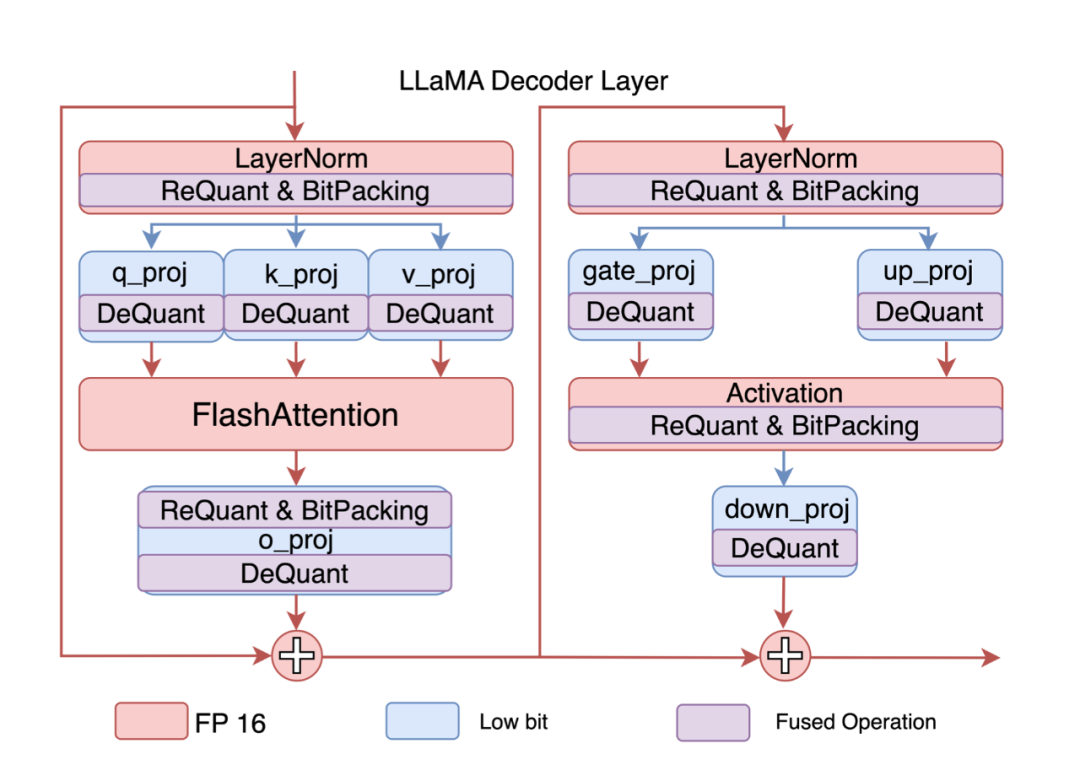
▲ 图6.（右）ABQKernel 构成 transformer block. ReQuant 和 DeQuant 分别表示在线量化和反量化操作，BitPacking 表示激活的在线布局转换操作

NVIDIA GPU 拥有许多称为流多处理器（SM）的处理单元，并使用大量线程并行执行计算任务。线程被构造为线程块，线程块成为 SM 上最小的调度执行单元。因此，计算目标被分解和映射到每个线程块上（称为 Thread Block Tile），以实现并行计算。

如图 6（a）所示，对于形状为 M×N×K 的 GEMM 任务，每个线程块负责计算一个 BM×BN 输出块，该输出块被分解为形状为 BM×BN×BK 的 K/BK 子 GEMM 任务。我们的推理引擎将位宽配置为 {p，q} 的量化矩阵乘法转换为 p*q 个二值化矩阵乘法的特殊累积，因此 Thread Block Tile 的真正计算任务是 p*BM×q*BN，整体计算流水如下所示：

首先，为了提高内存访问的连续性，我们提出 BitPacking 策略，将量化张量分解为 n 个二进制矩阵，其中 n 为量化位宽。以输入 X 为例，这意味着它的 bit 视角的内存布局由 [M，K，p] 变为 [p，M，K]。线程块内的所有线程共享相同的共享内存空间（shared memory，SMEM）。在每个线程块内，线程进一步组织成 warp，每个 warp 由 32 个连续的线程组成。

接下来，warp 协作地从全局内存（global memory，GL），加载当前的 Thread Block 需要计算的 Thread Block Tile 块所需的 A 矩阵（p*BM×BK）和 B 矩阵（BK×q*BN）数据并缓存在 SMEM 中。得益于 BitPacking，读取 pBM*BK 单比特 row-major 的 Tile 块和写入 p*BM*BK bit 到 SMEM 的过程是高效且连续的。

随后，由于 thread block 包含多个 warp，因此可以进一步将 Thread Block Tile 分解为 Warp Tile，实现 warp 级并行，每个 warp 的计算任务为 WM×WN。在计算准备阶段，将 A 矩阵（WM×WK，row-major）和 B 矩阵（WK×WN，col-major）独立从 SMEM 加载到 FR，随后将计算分解为 WARP_M_TILES*WARP_N_TILES 个 Tensor Core MMA（matrix-multiply-accumulate）运算。由于 A 和 B 是二值化矩阵，因此我们实际使用的是 Binary TensorCoreMMA（BMMA），其计算能力分别比 INT8 和 INT4 TensorCore 提升 8 倍和 4 倍。

所有 warp 协同完成 Thread BlockTile 计算，结果存储在每个 warp 的 c fragments 中，因此每个 warp 需要独立将计算结果写回 SMEM。

输出图块（p*BM × q*BN）在 SMEM 中执行全局缩减求和以获得最终的正确结果（BM × BN），其中每个 BM × BN 子图块需要乘以某个缩放因子。我们称此过程为 Bit Reduction。

最后一步，warp 协同地从 SMEM 加载最终结果并写回 GL 中的目标位置。

我们将上述计算过程实现为一个名为 ABQKernel 的 GPUKernel。如图 6（b）所示，ABQKernel 用于替换解码器层中的所有 gemm 操作，结合必要的 BitPacking、量化和反量化辅助操作，实现了 LLaMA 模型的任意量化推理。我们通过将辅助运算符融合到现有运算符中来精心管控量化运算符的开销，并且权重 BitPacking 是离线实现的，以提升效率。

此外，我们还运用了多种优化手段，包括 GEMV 消除、Bank Conflicts 消除、Computational and Pipeline 优化和 AutoKernelSearch。

3.4 GEMV 运算消除

▎Eliminate GEMV

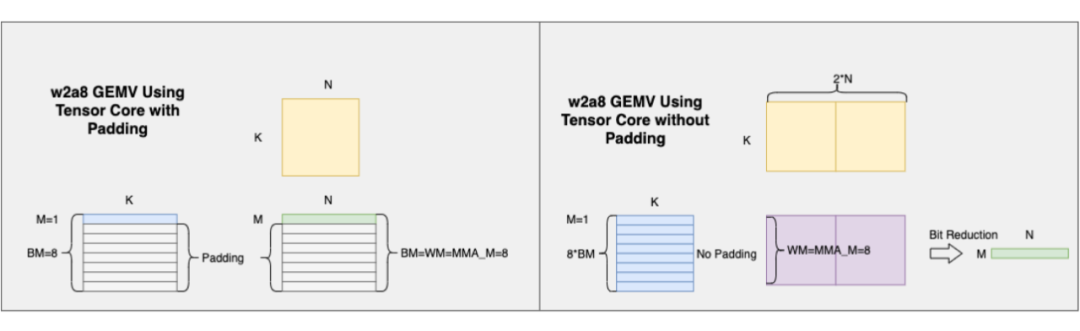
▲ 图7. GEMV 实质性转化为 GEMM 问题

LLM 类模型中 80% 的计算量和参数访存集中在 GEMM/GEMV 运算，解码阶段的 GEMV 是核心性能瓶颈。不失一般性地说，GEMV/GEMM 操作都可以使用 M、N、K 表示，其中两个相乘矩阵的大小为 M × K 和 K × N。

当 M=1 时，GEMM 问题会转换为 GEMV 问题，同时算子会从计算密集型转变为访存密集型。为了使用 Tensor Core 进行加速计算，通常会沿 M 维按 BM=8 进行分块，若 M<8 则进行 0 填充，导致冗余计算。

我们基于 BTC 的任意精度量化推理，通过将矩阵分解成若干个单比特的矩阵分量，把多个单比特的 GEMV 问题转换回 GEMM 问题，在利用 Tensor Core 的同时，减少甚至避免 padding 导致的冗余计算。

如图 7 所示的一个 w2a8 算子实现，相比于直接将 BM 填充至 8 再调用 Tensor Core 的方式，我们可以将 X 矩阵分解成 8 个子矩阵，若设 M=1，BM=1，WM=MMA_M=8，padding 的占比从 7/8=87.5% 降低至 0%。在其他精度的情况下，亦可以根据 M 的大小，通过调整 BM 的大小，减少甚至避免 padding 导致的冗余计算，提高 Tensor Core 的利用率。

3.5 BankConflict 消除

▎BankConflict Free

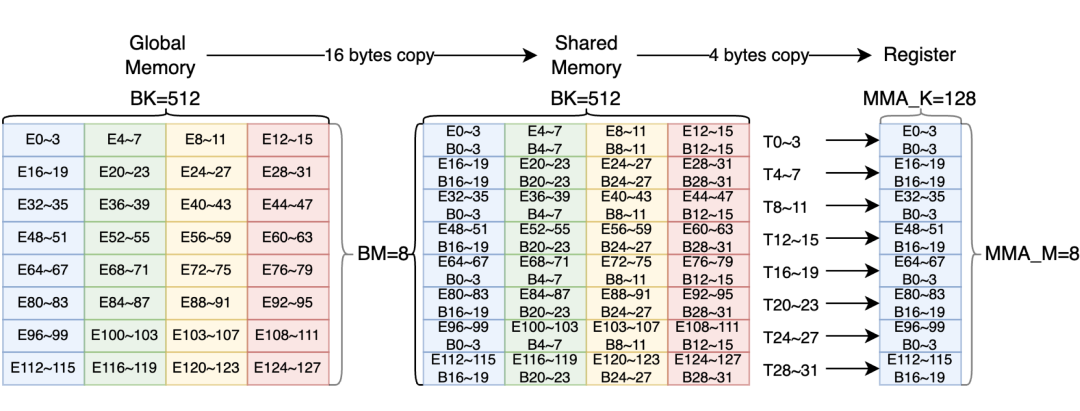
▲ 图8. 共享内存内发生 4 路 bank 冲突的访存模式，E 表示 int32 的一个元素，B 表示 bank，T 表示一个线程

BankConflicts 的存在是影响访存效率的一大因素，图 8 展示了 Bank 冲突发生的场景（BM=8,BK=512），其中 E 代表 int32 视角的元素（Element），B 代表 Bank，T 代表 Thread。

数据从全局内存拷贝至共享内存时，为了充分利用内存带宽，每个线程以 16Bytes 进行内存拷贝，此时 8x512bit 数据会分成 4 个阶段（Phase），每个阶段读取 128Bytes（即图中连续两行数据），所有阶段都不会发生 Bank 冲突。

数据从共享内存拷贝至寄存器时，由于 8x8x128 的 BMMA 以 32-bit 寄存器来存储矩阵 A（8x128 bit）和矩阵 B（8x128 bit），每个线程需要拷贝 4Bytes，拷贝一个矩阵块（同颜色块）时，线程 T0~3、T8~11、T16~19、T24~27 均会访问 B0~3，T4~7、T12~15、T20~23、T28~31 均会访问B16~19，此时发生 4 路 Bank 冲突，降低了访问效率。

如图 9 所示，我们采用了 swizzle 操作解决了这一问题。如上所述 8x512bit 数据会分成 4 个阶段（Phase），每个阶段 8 个线程完全访问 32 个 Bank（128 Bits），每个线程整体负责 16Bytes 访存，因此我们将连续两行作为一个整体进行坐标标定，每个线程负责访存的数据块（同颜色的 16Bytes 块）坐标为（irow, icol）。

例如 T0 负责访问的数据块为（0,0），T7 负责访问的数据块为（0,7），同理 T8 和 T15 访问的数据块坐标也是（0,0）和（0,7），在全局内存拷贝至共享内存时，对坐标进行 swizzle，本质上是应用 new_icol = irow ^ icol 的坐标变换，使同一个矩阵的 8x128bit 数据错落在不同的 32 个 Bank 中。

在共享内存拷贝至寄存器时，T0~31 访问的数据分别来自不同的 Bank，访问不同的矩阵块均不会发生 Bank 冲突，进而提高访存效率。

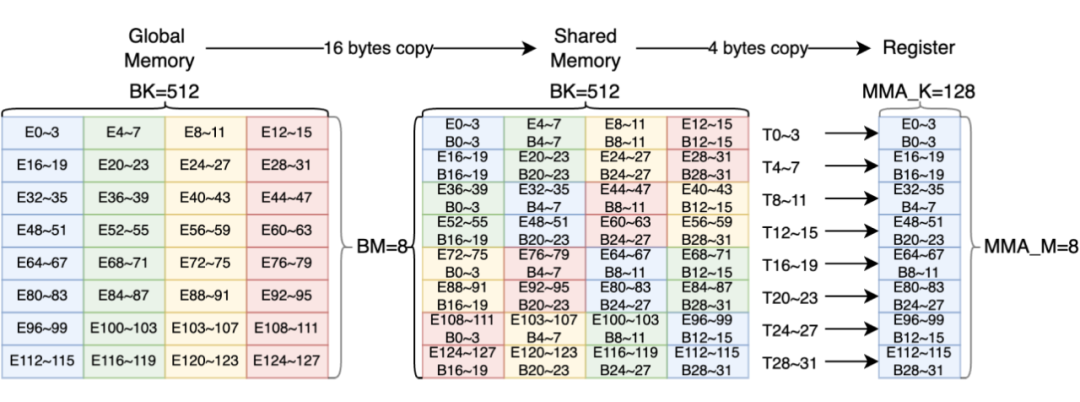
▲ 图9. 利用 swizzle 实现共享内存内无 bankconflicts

计算流水优化

▎Computational and Pipeline Optimization

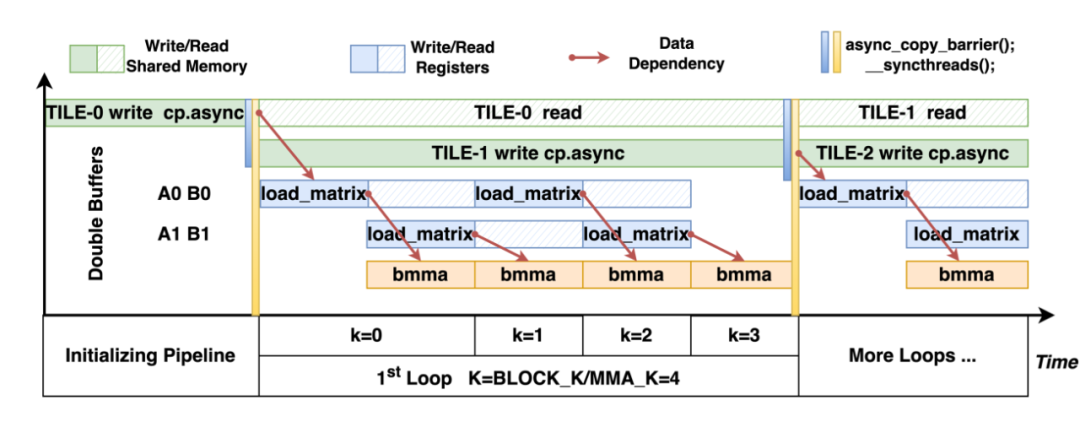
▲ 图10. 计算流水线的时空图

上图展示了我们在 SM80+ 架构上进行的计算流水优化。在共享内存级别，通过 cp.async 指令异步执行全局内存到共享内存的写入。在处理第一个循环前，发出同步来确保第一个循环所需要的数据 TILE-0 已经准备在共享内存中。在处理第一个循环时，第二个循环所需的数据 TILE-1 同时也会往共享内存当中写入。从而在计算第一个循环时掩盖掉第二个循环所需共享内存的访存耗时。

在寄存器级别，当 k=0 时，共享内存的 TILE-0 数据会被加载进第一组寄存器 A0、B0 中，同时 k=1 所需的数据也会同时进行预加载至寄存器 A1、B1。寄存器 A0、B0 的数据准备就绪后，会调用 bmma 对 A0、B0 进行计算。

当 k=1 时，bmma 所需的数据 A1、B1 已经在 k=0 时预加载，此时对 k=2 所需的数据进行预加载至寄存器 A0、B0，如此循环，从而实现在 Tensor Core bmma 计算的同时将数据从共享内存写入到寄存器，完成在 bmma 计算时掩盖掉寄存器的访存耗时。

3.6 自动算子搜索

▎Auto Kernel Search

为了在所有层级上更高效地利用 GPU 内存，在计算过程中采用分块策略至关重要。块大小对 GEMM 性能至关重要。在启动任意精度推理操作之前，我们会对不同的块大小进行性能测试，以选择最佳的实现方法。

对于经典的 GEMM 任务，M × N × K 问题通常在线程块级别上被分块为 BM × BN × BK，每个线程块在 warp 级别上进一步被分块为 WM × WN × WK。每个 warp 基于 GPU 模型支持的 Tensor Core块大小获取 MMA_M × MMA_N × MMA_K ，然后在获得这三个层级的块大小后，搜索不同的块形状。

在任意精度操作中，还需要考虑权重比特数（q）和激活比特数（p），因此搜索空间比经典 GEMM 更大。

给定 BTC 块大小为 MMA_M = 8, MMA_N = 8, MMA_K = 128，权重维度 warps 的数量为 W_WARPS_NUM = BN × q / WN，激活维度 warps 的数量为 X_WARPS_NUM = BM × p / WM，实际 warps 数量为1 ≤ X_WARPS_NUM × W_WARPS_NUM ≤ 32。

为了减少搜索空间，我们固定 WK = MMA_K = 128，并将 BK 的长度设置为 {128, 256, 384, 512}。由于单个线程块的共享内存和寄存器使用受限，BM、BN、BK、WM 和 WN 不能无限大。对于配置，搜索空间中候选实例的设计过程总结如下：

基于专家经验，确定搜索空间中想要进行测速的每个配置的 warps 的数量和布局。例如，X_WARPS_NUM × W_WARPS_NUM = 1 × 4。
基于计算任务的 M 维度和激活的量化位宽 p，确定在具有最小冗余填充的情况下，想要进行测速的每个配置的 Thread Block Tile大小（<BM, BN, BK>）。
根据 warps 的布局和 Thread Block Tile 大小，计算 warp 块的大小（<WM, WN, WK>）。最终，我们在不同平台执行速度测试，并采用速度最优的的并行配置。

Experiments

4.1 效果

实验结果表明：ABQ-LLM 在 LLaMA、LLaMA-2 系列模型上取得了优异的效果，在 weight-only 和 weight-activation 量化方面始终优于先前的 LLM 量化工作。这些结果彰显了 ABQ-LLM 的健壮性，能够适应多种量化配置和量化场景。

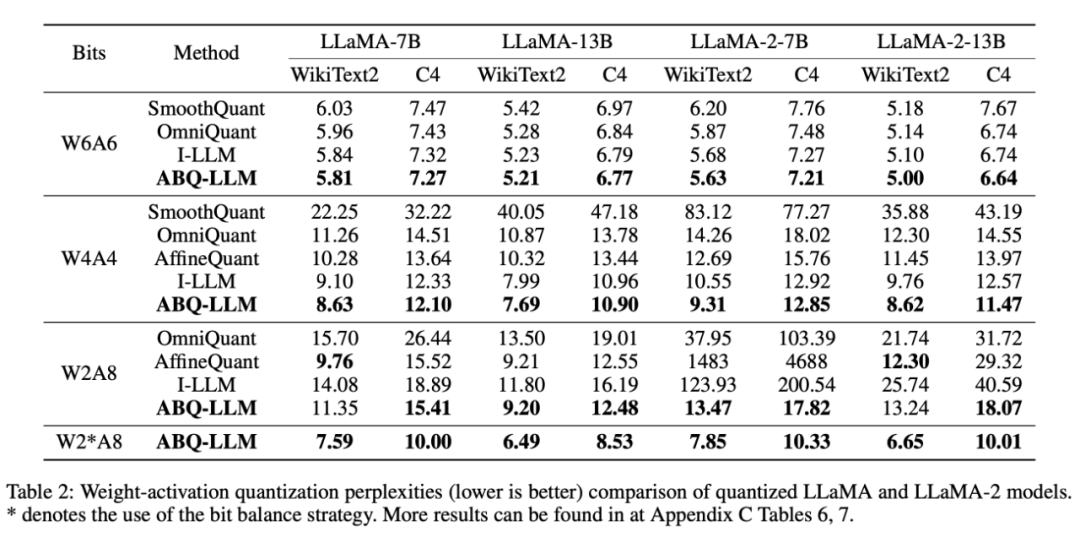
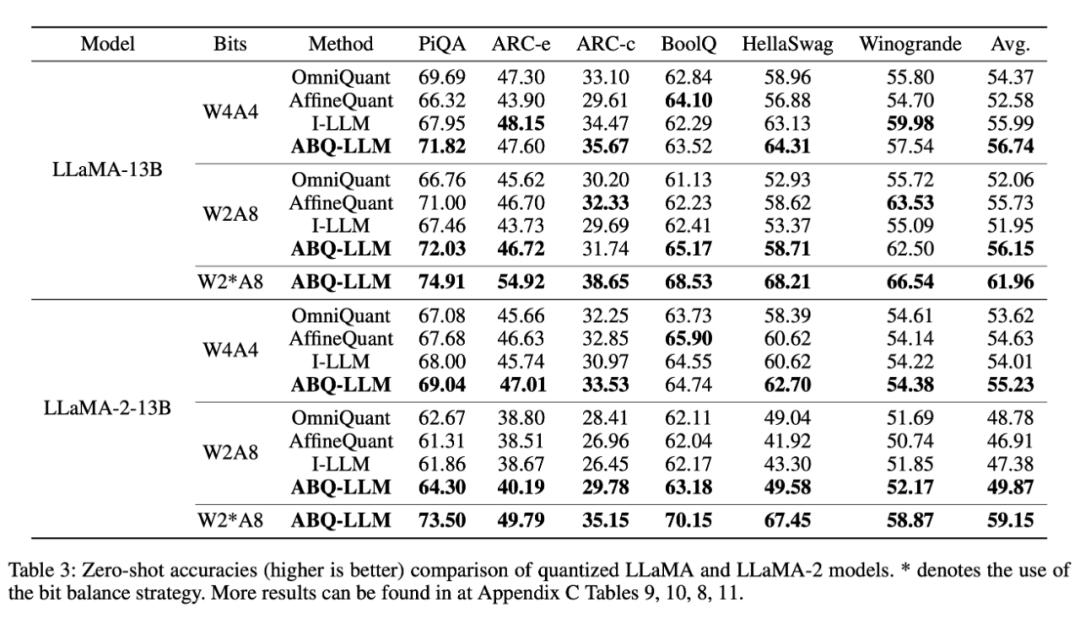
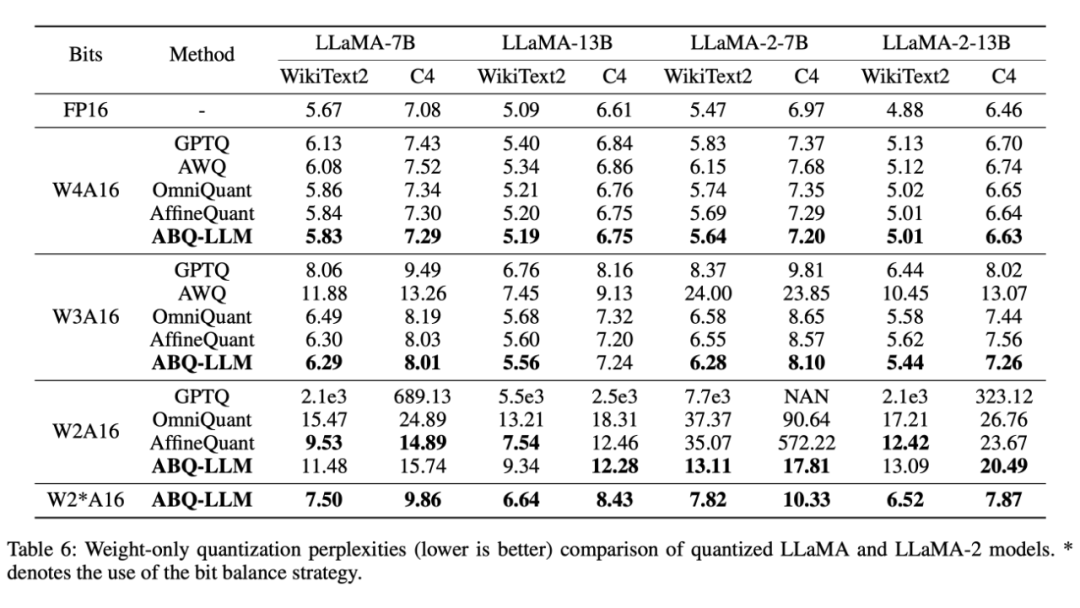
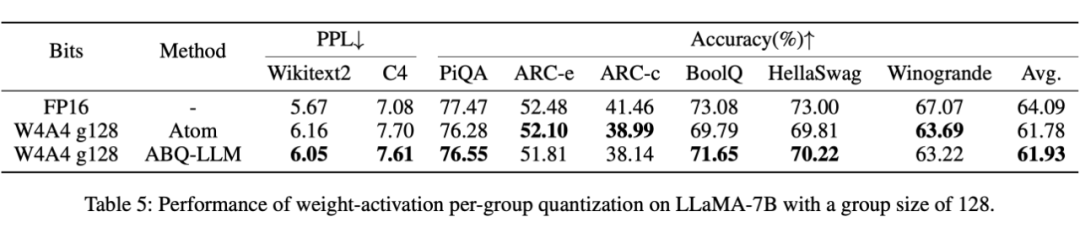
此外，ABQ-LLM 天然与 per-group 量化正交，而 per-group 量化也是当前主流量化推理引擎所采用的主流方式。下表的结果显示，当我们对 ABQ-LLM 施加分组大小为 128 的 per-group 量化时，我们的 W4A4 取得了与全精度模型相当的结果，同时超越了其他 per-group 量化的工作，例如 Atom 等，再次凸显出 ABQ-LLM 的健壮性。

4.2 性能

Kernel Benchmark：我们在 LLM 模型典型 GEMM 计算 shape 下对比 ABQKernel 和 cutlass/cublas 库内核的性能。值得注意的是，CUTLASS 仅支持 W4A4 和 W8A8，而 cuBLAS 仅支持 W8A8 进行量化操作。

图 11 显示了结果，表明我们的 ABQKernel 在所有矩阵大小上都实现了卓越的加速。具体来说，对于 W2A8 和 W2A4 等特殊位组合，我们的 ABQKernel 明显优于基线方法，因为 cuBLAS 和 CUTLASS 需要转换为 W8A8 和 W4A4 才能进行计算。在 W2A8 配置中，与使用 CUTLASS 和 cuBLAS 的 W8A8 相比，我们的吞吐量在尺寸（1, 4096）×（4096, 4096）上提高了 7.47 倍。

E2E Benchmark：将 ABQKernel 集成到 fastertransformer 中，并将其与 fastertransformer 的 FP16 实现和 SmoothQuant 的 INT8 实现进行比较。与 FP16 相比，我们的方案实现了 2.95 倍的推理加速和 4.8 倍的内存压缩，同时在 LLaMA-30B 模型上仅需要 10GB 的内存进行推理，这低于使用 FP16 的 LLaMA-7B 所需的内存。

此外，与 SmoothQuant 相比，我们的方案实现了 1.6倍的加速和 2.7 倍的内存压缩增益，这是一个了不起的成就，因为 SmoothQuant 已经实现了很多细致的优化。

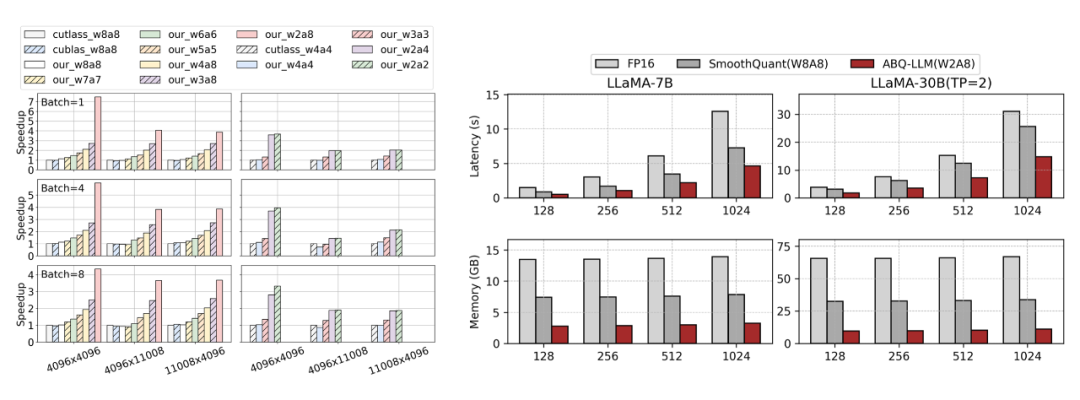
▲ 图11.（左）算子级性能对比，ABQKernel 可以有效地将位宽收益转化为加速收益.（右）fastertransformer 框架中的端到端性能对比

我们还对 ABQ-LLM 进行了全面的测评，将其与主流的算法 QServe [3]、Atom [4]、QuaRot [5]、AffineQuant [6]、GPTQ [7]、AWQ [8]、OmniQuant [9]、I-LLM [10]、SmoothQuant [11] 进行了比较，欢迎查看我们的全文 ABQ-LLM。

更多阅读