ICP算法；RABSAC鲁棒估计模型；

想要实现点的对应。

求解的目标函数：目标就是得到R,t

求解最优变换

首先计算质心，然后从两个点集中分别减去对应的质心。
通过SVD分解求得最优变换，


如果知道正确的点对应，那么两个点集之间的相对旋转和 平移有闭合解
在ICP中，假设最近的点为对应点 已经证明，如果初始点‚足够的近‛，可以保证收敛性

ICP流程

首先选取数据中的一些点作为候选的匹配点；在每一步迭代中，通过几种匹配方法(最近邻等)找到两个数据集中的对应点对；在已知点对的情况下，优化目标函数，求R/t; 然后求E(R，t)，如何E大于阈值，就继续基于目前的位置进行迭代优化。
实质就是不断地调整点的位置来匹配，最后小于阈值，则说明匹配好。

—只是局部最优，因为匹配点不一定是准确的。
点集选取：
选择所有点 • 均匀采样(Uniform Sampling) • 随机采样(Random Sampling) • 法方向空间均匀采样(Normal-space Uniform Sampling)

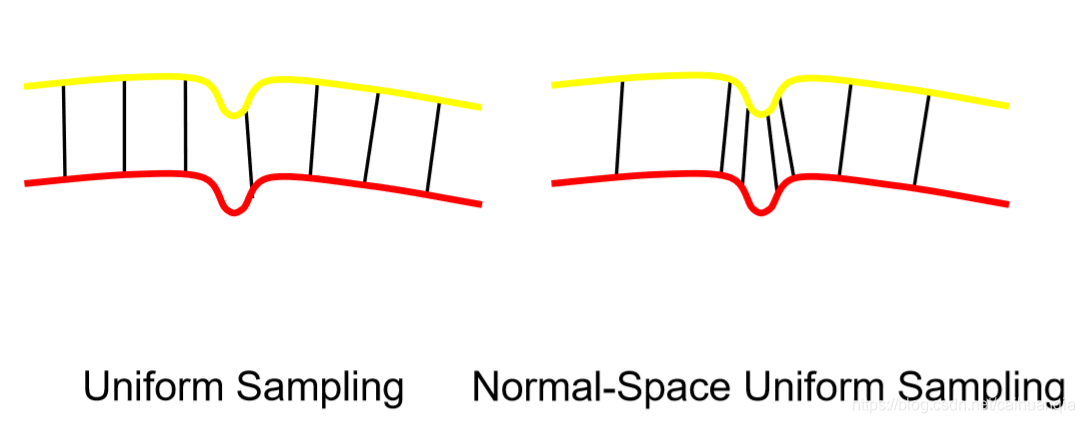
点集匹配：
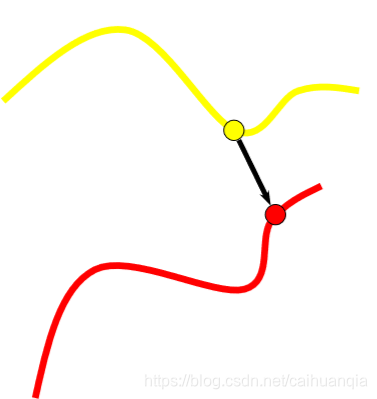
最近邻点 (Closest point)
• 法方向最近邻点 (Normal shooting)
• 投影法 (Projection)
最近邻点：稳定但是速度慢。

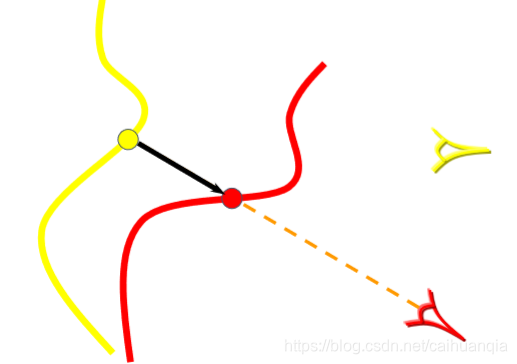
法方向最近邻点 ：平滑曲面效果好，但对噪音敏感

投影法：搜索对应点速度快

点集对应权重：

鲁棒匹配问题——原因是外点的干扰

有一些外点的存在导致拟合出现问题。干扰前面所说的R和t，导致变换之后仍然无法匹配。
重要：

RABSAC模型：基于概率论和随机的理论，尽管样本很多，但是其实需要抽取的不需要很多，所以可以在很短的时间内，较少的计算就可以得到较好的结果！！！

比如一条平面中的直线需要两个点。随机抽取两个点就是一条直线，算数据点集合中距离这条直线的距离，如果距离充分小，那么这些距离充分小的点就组成一致集。如果一致集的点的个数充分多，则用一致集中的点，重新估计拟合模型；相反，如果不太多，就返回再随机抽取新的样本，再判断一致集。。。。。。
经过K次随机抽样，如果确实没有找到大于阈值的，那么就在K中找到一个最好的。