LeetCode 52. N-Queens II 解题报告

LeetCode 52. N-Queens II 解题报告

题目描述

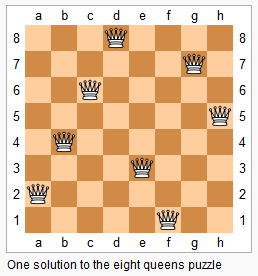
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.
Given an integer n, return the total number of distinct solutions.

---

示例

1
return 1
4
return 2

---

限制条件

没有明确给出.

---

解题思路

我的思路：

对于N皇后的问题，求解的过程如下：
1.从i行的第j列开始，逐列判断是否能够放置棋子。
2.如果i行的j列能够放置棋子，我们就对i+1行重复第1步
3.如果i行所有列都放不了棋子，回到i-1行，从新的列开始重复第1步
4.如果在最后一行也找到了放棋子的列，我们就找到了一种解法，然后便尝试在这一行找新的能放棋子的列（寻找新的结果）
5.如果在第一行也找不到放棋子的列，就表示没有更多的解法，于是返回至今找到的解法的数目。
其中第3步体现了回溯的思想。

代码的实现就是按照以上的步骤分块进行：
1.对i行放置棋子：我们需要做的就是判断i行的每一列能不能放棋子，能就放置棋子，不能就尝试下一列，对应着步骤1。所以直接一个循环就行：j为列索引，board表示棋盘，是一维数组，索引表示行，数组元素表示列，即board[0] = 1表示在第0行的第1列放置了棋子；isValid函数用于判断能否在i行j列放棋子。

2.当放不了棋子时，就有两种情况，（1）是第一行也放不了棋子，所以我们要结束寻找的过程，对应着步骤5，（2）是其它的行放不了棋子，我们就回到上一行，并且在上一行的新列开始重新放棋子，对应着步骤3。代码如下所示：NULLVALUE是预先设置的无效值，如果board[i]等于NULLVALUE就表明放不了棋子，else条件中的语句就是回溯的关键。

3.当发现在最后一行也找到了放置棋子的列，我们就记录下这次结果，然后尝试在最后一行的剩下列找新的结果，对应着步骤4。代码如下：

通过把第二个代码放置于第三块代码之前，我们避免了判断最后一行是否能够放置棋子，如果前面的行不能放置棋子，就会进入到第二个代码，只有当前面的行都找到了放置位置，才会到达第三个代码，所以只要简单判断i是否等于最后一行即可。

第三个代码中最后的i++对应着步骤2。之所以放在这里，是因为第二跟第三个代码里的判断都是针对当前的i行，如果在第一个代码中就自增i，那么第二跟第三代码中判断的就不是当前的行，而是下一行，这显然是不合理的。

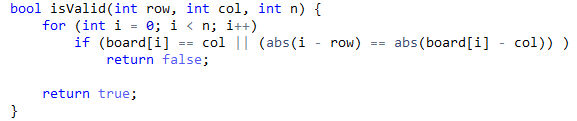
4.除了上面的三块代码，我们还留了一个尾巴，那就是isValid函数。在这个函数中，我们要判断i行j列是否能够放棋子，不能放的条件是，与之前的棋子同列或是与之前的棋子同对角线，满足两个条件之前就返回false。所以代码如下：

最后把所有代码合并一起就成了解题的代码了，下面给出的代码里isValid函数的函数名跟参数会不同，是我后来为了好看一些修改了一下，关键的地方与上面讲的是一样。建议对着代码，好好体味整个运行过程。

---

代码

我的代码

class Solution {
public:
    int totalNQueens(int n) {
        const int INVALID = 1000;
        vector<int> board(n, INVALID);
        int i = 0;
        int j = 0;
        int result = 0;

        while (i < n) {
            while (j < n) {
                if (valid(board, i, j)) {
                    board[i] = j;
                    j = 0;
                    break;
                } else {
                    j++;
                }
            }

            if (board[i] == INVALID) {
                if (!i) {
                    break;
                }  else {
                    i--;
                    j = board[i] + 1;
                    board[i] = INVALID;
                    continue;
                }
            }

            if (i == n - 1) {
                result++;
                j = board[i];
                board[i] = INVALID;
                j++;
                continue;
            } 

            i++;
        }

        return result;
    }

    bool valid(vector<int> &b, int row, int col) {
        for (int i = 0; i < b.size(); i++)
            if ((b[i] == col) || (abs(row - i) == abs(col - b[i])))
                return false;
        return true;
    }    
};

---

总结

N皇后的题目，以前就见到过了好几遍，每次都没有认真花时间去想，这次总算是好好地把这道历史遗留问题给搞定了。相信下次再遇到，也能够完整的再实现一次。
搞定了这个坑，专心做其他的事了，努力努力！加油加油！