编辑本段空间复杂度
编辑本段时间与空间复杂度比较
在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,它考察当输入值大小趋近无穷时的情况。举例,如果一个算法对于任何大小为 的输入,它至多需要
的输入,它至多需要 的时间运行完毕,那么它的渐近时间复杂度是
的时间运行完毕,那么它的渐近时间复杂度是 。
。
计算时间复杂度的过程,常常需要分析一个算法运行过程中需要的基本操作,计量所有操作的数量。通常假设一个基本操作可在固定时间内完成,因此总运行时间和操作的总数量最多相差一个常量系数。
有时候,即使对于大小相同的输入,同一算法的效率也可能不同。因此,常对最坏时间复杂度进行分析。最坏时间复杂度定义为对于给定大小  的任何输入,某个算法的最大运行时间,记为
的任何输入,某个算法的最大运行时间,记为 。通常根据
。通常根据 对时间复杂度进行分类。比如,如果对某个算法有
对时间复杂度进行分类。比如,如果对某个算法有 ,则称其具有线性时间。如有
,则称其具有线性时间。如有 ,则称其具有指数时间。
,则称其具有指数时间。
目录
[隐藏]常见时间复杂度列表[编辑]
以下是一些常见时间复杂度的例子。
| 名称 | 复杂度类 | 运行时间( ) ) | 运行时间举例 | 算法举例 |
|---|---|---|---|---|
| 常数时间 |  | 10 | 判断一个二进制数的奇偶 | |
| 反阿克曼时间 |  | 并查集的单个操作的平摊时间 | ||
| 迭代对数时间 | 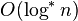 | en:Cole-Vishkin algorithm | ||
| 对数对数时间 |  | 有界优先队列的单个操作[1] | ||
| 对数时间 | DLOGTIME |  | 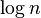 , , | 二分搜索 |
| 幂对数时间 |  | 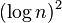 | ||
| (小于1次)幂时间 |  ,其中 ,其中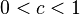 | 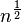 , , | K-d树的搜索操作 | |
| 线性时间 |  |  | 无序数组的搜索 | |
| 线性迭代对数时间 |  | Raimund Seidel的三角分割多边形算法 | ||
| 线性对数时间 |  |  , , | 最快的比较排序 | |
| 二次时间 |  |  | 冒泡排序、插入排序 | |
| 三次时间 |  | 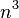 | 矩阵乘法的基本实现,计算部分相关性 | |
| 多项式时间 | P | 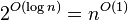 |  , , , , | 线性规划中的en:Karmarkar's algorithm, AKS质数测试 |
| 准多项式时间 | QP |  |  , , | |
| 次指数时间(第一定义) | SUBEXP |  ,对任意的 ε > 0 ,对任意的 ε > 0 |  | Assuming complexity theoretic conjectures, BPP is contained in SUBEXP.[2] |
| 次指数时间(第二定义) | 2o(n) | 2n1/3 | Best-known algorithm for integer factorization and graph isomorphism | |
| 指数时间 | E | 2O(n) | 1.1n, 10n | 使用动态规划解决旅行推销员问题 |
| 阶乘时间 | O(n!) | n! | 通过暴力搜索解决旅行推销员问题 | |
| exponential time | EXPTIME | 2poly(n) | 2n, 2n2 | |
| double exponential time | 2-EXPTIME | 22poly(n) | 22n | Deciding the truth of a given statement in Presburger arithmetic |
常数时间[编辑]
若对于一个算法,  的上界与输入大小无关,则称其具有常数时间,记作
的上界与输入大小无关,则称其具有常数时间,记作 时间。一个例子是访问数组中的单个元素,因为访问它只需要一条指令。但是,找到无序数组中的最小元素则不是,因为这需要遍历所有元素来找出最小值。这是一项线性时间的操作,或称
时间。一个例子是访问数组中的单个元素,因为访问它只需要一条指令。但是,找到无序数组中的最小元素则不是,因为这需要遍历所有元素来找出最小值。这是一项线性时间的操作,或称 时间。但如果预先知道元素的数量并假设数量保持不变,则该操作也可被称为具有常数时间。
时间。但如果预先知道元素的数量并假设数量保持不变,则该操作也可被称为具有常数时间。
虽然被称为“常数时间”,运行时间本身并不必须与问题规模无关,但它的上界必须是与问题规模无关的确定值。举例,“如果 a > b 则交换 a、b 的值”这项操作,尽管具体时间会取决于条件“a > b”是否满足,但它依然是常数时间,因为存在一个常量 t 使得所需时间总不超过 t。
以下是一个常数时间的代码片段:
int index = 5;
int item = list[index];
if (condition true) then
perform some operation that runs in constant time
else
perform some other operation that runs in constant time
for i = 1 to 100
for j = 1 to 200
perform some operation that runs in constant time
如果  ,其中
,其中 是一个常数,这记法等价于标准记法
是一个常数,这记法等价于标准记法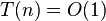 。
。
对数时间[编辑]
若算法的 T(n) = O(log n),则称其具有对数时间。由于计算机使用二进制的记数系统,对数常常以2为底(即log2n,有时写作 lg n)。然而,由对数的换底公式,logan 和 logb n只有一个常数因子不同,这个因子在大O记法中被丢弃。因此记作O(log n),而不论对数的底是多少,是对数时间算法的标准记法。
A O(log n) algorithm is considered highly efficient, as the operations per instance required to complete decrease with each instance.
A very simple example of this type of f(n) is an algorithm that cuts a string in half. It will take O(log n) time (n being the length of the string) since we chop the string in half before each print. This means, in order to increase the number of prints, we have to double the length of the string.
// 递归输出一个字符串的右半部分 var right = function(str) { var length = str.length; // 辅助函数 var help = function(index) { // 递归情况:输出右半部分 if(index < length){ // 输出从 index 到数组末尾的部分 console.log(str.substring(index, length)); // 递归调用:调用辅助函数,将右半部分作为参数传入 help(Math.ceil((length + index)/2)); } // 基本情况:什么也不做 } help(0); }
幂对数时间[编辑]
An algorithm is said to run in polylogarithmic time if T(n) = O((logn)k), for some constant k. For example, matrix chain ordering can be solved in polylogarithmic time on aParallel Random Access Machine.[3]
Sub-linear time[编辑]
An algorithm is said to run in sub-linear time (often spelledsublinear time) if T(n) = o(n). In particular this includes algorithms with the time complexities defined above, as well as others such as the O(n½)Grover's search algorithm.
Typical algorithms that are exact and yet run in sub-linear time use parallel processing (as the NC1 matrix determinant calculation does),non-classical processing (as Grover's search does), or alternatively have guaranteed assumptions on the input structure (as the logarithmic timebinary search and many tree maintenance algorithms do). However, languages such as the set of all strings that have a 1-bit indexed by the first log(n) bits may depend on every bit of the input and yet be computable in sub-linear time.
The specific term sublinear time algorithm is usually reserved to algorithms that are unlike the above in that they are run over classical serial machine models and are not allowed prior assumptions on the input.[4] They are however allowed to be randomized, and indeed must be randomized for all but the most trivial of tasks.
As such an algorithm must provide an answer without reading the entire input, its particulars heavily depend on the access allowed to the input. Usually for an input that is represented as a binary stringb1,...,bk it is assumed that the algorithm can in time O(1) request and obtain the value ofbi for any i.
Sub-linear time algorithms are typically randomized, and provide only approximate solutions. In fact, the property of a binary string having only zeros (and no ones) can be easily proved not to be decidable by a (non-approximate) sub-linear time algorithm. Sub-linear time algorithms arise naturally in the investigation ofproperty testing.
线性时间[编辑]
如果一个算法的时间复杂度为O(n),则称这个算法具有线性时间,或 O(n) 时间。 非正式地说,这意味着对于足够大的输入,运行时间增加的大小与输入成线性关系。例如,一个计算列表所有元素的和的程序,需要的时间与列表的长度成正比。这个描述是稍微不准确的,因为运行时间可能显著偏离一个精确的比例,尤其是对于较小的n。
Linear time is often viewed as a desirable attribute for an algorithm. Much research has been invested into creating algorithms exhibiting (nearly) linear time or better. This research includes both software and hardware methods. In the case of hardware, some algorithms which, mathematically speaking, can never achieve linear time with standardcomputation models are able to run in linear time. There are several hardware technologies which exploitparallelism to provide this. An example is content-addressable memory. This concept of linear time is used in string matching algorithms such as theBoyer-Moore Algorithm and Ukkonen's Algorithm.
线性对数(准线性)时间[编辑]
A linearithmic function (portmanteau oflinear and logarithmic) is a function of the form n · logn (i.e., a product of a linear and a logarithmic term). An algorithm is said to run in linearithmic time ifT(n) = O(n log n). Compared to other functions, a linearithmic function is ω(n), o(n1+ε) for every ε > 0, and Θ(n · logn). Thus, a linearithmic term grows faster than a linear term but slower than any polynomial inn with exponent strictly greater than 1.
An algorithm is said to run in quasilinear time if T(n) =O(n logk n) for any constantk. Quasilinear time algorithms are also o(n1+ε) for every ε > 0, and thus run faster than any polynomial inn with exponent strictly greater than 1.
In many cases, the n · log n running time is simply the result of performing a Θ(logn) operation n times. For example, binary tree sort creates a binary tree by inserting each element of the n-sized array one by one. Since the insert operation on aself-balancing binary search tree takes O(log n) time, the entire algorithm takes linearithmic time.
比较排序s require at least linearithmic number of comparisons in the worst case because log(n!) = Θ(n logn), by Stirling's approximation. They also frequently arise from the recurrence relation T(n) = 2 T(n/2) + O(n).
Some famous algorithms that run in linearithmic time include:
- Comb sort, in theaverage and worst case
- Quicksort in the average case
- Heapsort,merge sort, introsort, binary tree sort, smoothsort, patience sorting, etc. in the worst case
- Fast Fourier transforms
- Monge array calculation
Sub-quadratic time[编辑]
An algorithm is said to be subquadratic time if T(n) = o(n2).
For example, most naïve comparison-based sorting algorithms are quadratic (e.g. insertion sort), but more advanced algorithms can be found that are subquadratic (e.g.Shell sort). No general-purpose sorts run in linear time, but the change from quadratic to sub-quadratic is of great practical importance.
多项式时间[编辑]
An algorithm is said to be of polynomial time if its running time isupper bounded by a polynomial expression in the size of the input for the algorithm, i.e., T(n) = O(nk) for some constantk.[5][6]Problems for which a polynomial time algorithm exists belong to the complexity class P, which is central in the field ofcomputational complexity theory. Cobham's thesis states that polynomial time is a synonym for "tractable", "feasible", "efficient", or "fast".[7]
Some examples of polynomial time algorithms:
- The quicksort sorting algorithm on n integers performs at most
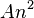 operations for some constantA. Thus it runs in time
operations for some constantA. Thus it runs in time  and is a polynomial time algorithm.
and is a polynomial time algorithm. - All the basic arithmetic operations (addition, subtraction, multiplication, division, and comparison) can be done in polynomial time.
- Maximum matchings ingraphs can be found in polynomial time.
强多项式时间与弱多项式时间[编辑]
In some contexts, especially in optimization, one differentiates between strongly polynomial time andweakly polynomial time algorithms. These two concepts are only relevant if the inputs to the algorithms consist of integers.
Strongly polynomial time is defined in the arithmetic model of computation. In this model of computation the basic arithmetic operations (addition, subtraction, multiplication, division, and comparison) take a unit time step to perform, regardless of the sizes of the operands. The algorithm runs in strongly polynomial time if [8]
- the number of operations in the arithmetic model of computation is bounded by a polynomial in the number of integers in the input instance; and
- the space used by the algorithm is bounded by a polynomial in the size of the input.
Any algorithm with these two properties can be converted to a polynomial time algorithm by replacing the arithmetic operations by suitable algorithms for performing the arithmetic operations on aTuring machine. If the second of the above requirement is not met, then this is not true anymore. Given the integer (which takes up space proportional to n), it is possible to compute
(which takes up space proportional to n), it is possible to compute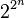 with n multiplications usingrepeated squaring. However, the space used to represent
with n multiplications usingrepeated squaring. However, the space used to represent 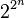 is proportional to
is proportional to , and thus exponential rather than polynomial in the space used to represent the input. Hence, it is not possible to carry out this computation in polynomial time on a Turing machine, but it is possible to compute it by polynomially many arithmetic operations.
, and thus exponential rather than polynomial in the space used to represent the input. Hence, it is not possible to carry out this computation in polynomial time on a Turing machine, but it is possible to compute it by polynomially many arithmetic operations.
Conversely, there are algorithms which run in a number of Turing machine steps bounded by a polynomial in the length of binary-encoded input, but do not take a number of arithmetic operations bounded by a polynomial in the number of input numbers. TheEuclidean algorithm for computing the greatest common divisor of two integers is one example. Given two integers  and
and the running time of the algorithm is bounded by
the running time of the algorithm is bounded by Turing machine steps. This is polynomial in the size of a binary representation of
Turing machine steps. This is polynomial in the size of a binary representation of and
and as the size of such a representation is roughly
as the size of such a representation is roughly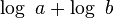 . At the same time, the number of arithmetic operations cannot be bound by the number of integers in the input (which is constant in this case, there is always only two integers in the input). Due to the latter observation, the algorithm does not run in strongly polynomial time. Its real running time depends on the magnitudes of
. At the same time, the number of arithmetic operations cannot be bound by the number of integers in the input (which is constant in this case, there is always only two integers in the input). Due to the latter observation, the algorithm does not run in strongly polynomial time. Its real running time depends on the magnitudes of and
and and not only on the number of integers in the input.
and not only on the number of integers in the input.
An algorithm which runs in polynomial time but which is not strongly polynomial is said to run inweakly polynomial time.[9] A well-known example of a problem for which a weakly polynomial-time algorithm is known, but is not known to admit a strongly polynomial-time algorithm, islinear programming. Weakly polynomial-time should not be confused with pseudo-polynomial time.
空 间 复 杂 度:
编辑本段时间与空间复杂度比较























 398
398

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








