数据结构-图实验

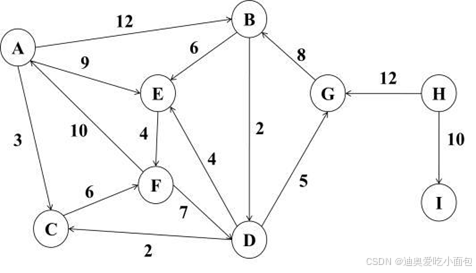
（1）基于图的深度优先搜索策略写一个算法，判别以邻接表方式存储的有向图中是否存在由顶点vi到顶点vj的路径（i!=j）。实例见上图。

（2）基于图的广度优先搜索策略写一个算法，判别以邻接表方式存储的有向图中是否存在由顶点vi到顶点vj的路径（i!=j）。实例见上图。

（3）以邻接表为存储结构实现从源点到其余各顶点的最短路径的Dijkstra算法，要求输出最短路径及其长度。实例见上图。

/*AdjMatrixDirNetwork.h*/
#ifndef ADJMATRIX_DIR_NETWORK_H
#define ADJMATRIX_DIR_NETWORK_H
#include <iostream>
#define DEFAULT_INFINITY 500
#define DEFAULT_SIZE 10
using namespace std;

enum VisitStatus { VISIT, UNVISIT };

class AdjMatrixDirNetwork    //顶点为字符型
{
public:
	AdjMatrixDirNetwork(int vertexMaxNum = DEFAULT_SIZE, int infinite = DEFAULT_INFINITY);  //默认构造函数，创建一个空图
	AdjMatrixDirNetwork(char* vexs, int vertexNum, int vertexMaxNum = DEFAULT_SIZE, int infinite = DEFAULT_INFINITY);
	~AdjMatrixDirNetwork();
	void InsertArc(int vex1, int vex2, int weight);   //输入合法，vex1与vex2小于vexNum，vex1!=vex2，不考虑平行边
	char GetElem(int vex);
	int GetVexNum();
	int GetArcNum();
	int GetWeight(int vex1, int vex2);
	int GetInfinity();
	int FirstAdjVex(int vex);   //返回顶点vex的第一个邻接顶点的序号，若没有则返回-1
	int NextAdjVex(int vex, int vex2);   //返回顶点vex的相对于vex2的下一个邻接顶点的序号，若没有则返回-1
	void Display();
	VisitStatus GetTag(int vex);   //输入合法
	int SetTag(int vex, VisitStatus _tag);  //返回状态

private:
	char* vertexes;
	VisitStatus* tag;
	int** arcs;
	int vexNum, vexMaxNum, arcNum;
	int infinity;
};

AdjMatrixDirNetwork::AdjMatrixDirNetwork(int vertexMaxNum, int infinite)
{
	vexMaxNum = vertexMaxNum;
	vexNum = 0;
	arcNum = 0;
	infinity = infinite;
	vertexes = new char[vexMaxNum];
	tag = new VisitStatus[vexMaxNum];
	arcs = new int* [vexMaxNum];
	for (int i = 0; i < vexMaxNum; i++)
		arcs[i] = new int[vexMaxNum];
}

AdjMatrixDirNetwork::AdjMatrixDirNetwork(char* vexs, int vertexNum, int vertexMaxNum, int infinite)
{
	vexMaxNum = vertexMaxNum;
	vexNum = vertexNum;
	infinity = infinite;
	arcNum = 0;
	vertexes = new char[vexMaxNum];
	tag = new VisitStatus[vexMaxNum];
	arcs = new int* [vexMaxNum];
	for (int i = 0; i < vexMaxNum; i++)
		arcs[i] = new int[vexMaxNum];
	for (int i = 0; i < vexMaxNum; i++)
	{
		vertexes[i] = vexs[i];
		tag[i] = UNVISIT;
		for (int j = 0; j < vexMaxNum; j++)
			arcs[i][j] = infinity;
	}
}

AdjMatrixDirNetwork::~AdjMatrixDirNetwork()
{
	if (vertexes != NULL)
		delete[] vertexes;
	if (tag != NULL)
		delete[] tag;
	if (arcs != NULL)
	{
		for (int i = 0; i < vexNum; i++)
			delete[] arcs[i];
		delete[] arcs;
	}
}

void AdjMatrixDirNetwork::InsertArc(int vex1, int vex2, int weight)
{
	arcs[vex1][vex2] = weight;
	arcNum++;
}

char AdjMatrixDirNetwork::GetElem(int vex)
{
	return vertexes[vex];
}

int AdjMatrixDirNetwork::GetVexNum()
{
	return vexNum;
}

int AdjMatrixDirNetwork::GetArcNum()
{
	return arcNum;
}

int AdjMatrixDirNetwork::GetWeight(int vex1, int vex2)
{
	return arcs[vex1][vex2];
}

int AdjMatrixDirNetwork::GetInfinity()
{
	return infinity;
}

int AdjMatrixDirNetwork::FirstAdjVex(int vex)
{
	for (int i = 0; i < vexNum; i++)
		if (arcs[vex][i] != infinity)
			return i;
	return -1;
}

int AdjMatrixDirNetwork::NextAdjVex(int vex, int vex2)
{
	for (int i = vex2 + 1; i < vexNum; i++)
		if (arcs[vex][i] != infinity)
			return i;
	return -1;
}

void AdjMatrixDirNetwork::Display()
{
	if (vexNum != 0)
	{
		for (int i = 0; i < vexNum; i++)
		{
			cout << "[ ";
			for (int j = 0; j < vexNum; j++)
				cout << arcs[i][j] << " ";
			cout << "]" << endl;
		}
	}
}

VisitStatus AdjMatrixDirNetwork::GetTag(int vex)
{
	return tag[vex];
}

int AdjMatrixDirNetwork::SetTag(int vex, VisitStatus _tag)
{
	if (vex >= vexNum)
		return 0;
	tag[vex] = _tag;
	return 1;
}
/*Node.h*/
#pragma once
#include<iostream>
using namespace std;

template <class DataType>
class Node
{
public:
	DataType data;
	Node<DataType>* next;
	Node() { next = NULL; }
	Node(DataType e, Node<DataType>* link = NULL)
	{
		data = e; next = link;
	}
};
/*LinkQueue.h*/
#pragma once
#ifndef _LINKQUEUE_H
#define _LINKQUEUE_H
#include "Node.h"	
template<class DataType>
class LinkQueue {
protected:
	Node<DataType>* front, * rear;	//队头与队尾指针
public:
	LinkQueue();				//构造函数
	virtual ~LinkQueue();			//析构函数
	bool IsEmpty() const;			//判断队列是否为空
	void Clear();				//清空队列
	int EnQueue(const DataType e);	//入队
	int DelQueue(DataType& e);	//出队
};
template<class DataType>
LinkQueue<DataType>::LinkQueue()
{
	rear = front = new Node<DataType>;
}
template <class DataType>
LinkQueue<DataType>::~LinkQueue() {
	Clear();
	delete front;
}

template<class DataType>
bool LinkQueue<DataType>::IsEmpty() const
{
	return front == rear;
}

template<class DataType>
void LinkQueue<DataType>::Clear()
{
	Node<DataType>* p = front->next;
	while (p) {
		front->next = p->next;
		delete p;
		p = front->next;
	}
}

template<class DataType>
int LinkQueue<DataType>::EnQueue(const DataType e) {
	Node<DataType>* p;
	p = new Node<DataType>(e);
	if (p)
	{
		rear->next = p;
		rear = rear->next;
		return 1;
	}

	else
		return 0;
}

template<class DataType>
int LinkQueue<DataType>::DelQueue(DataType& e) {
	if (IsEmpty())
		return 0;
	else
	{
		Node<DataType>* p = front->next;
		e = p->data;
		front->next = p->next;
		if (rear == p)
			rear = front;
		delete p;
		return 1;
	}
}
#endif

（1）

/*DFSpath.h*/
#include "AdjMatrixDirNetwork.h"
#include <iostream>
using namespace std;

void DFS(AdjMatrixDirNetwork& g, int v1, int v2,int &flag) {
    char e;
    g.SetTag(v1, VISIT);
    e = g.GetElem(v1);
    if (e == g.GetElem(v2))
        flag =1;
    for (int w = g.FirstAdjVex(v1); w != -1; w = g.NextAdjVex(v1, w))
    {
        if (g.GetTag(w) == UNVISIT)
            DFS(g, w, v2,flag);
    }
}

bool DFSpath(AdjMatrixDirNetwork& g, int v1, int v2) {
    int vexNum = g.GetVexNum();
    if (v1 < 0 || v1 >= vexNum)
    {
        cout << "v1取值不合法!" << endl;
        return 0;
    }
    if (v2 < 0 || v2 >= vexNum)
    {
        cout << "v2取值不合法!" << endl;
        return 0;
    }
    if (v1 == v2)
    {
        cout << "v1与v2不能相等!" << endl;
        return 0;
    }
    int flag = 0;
    for (int v = 0; v < vexNum; v++)
        g.SetTag(v, UNVISIT);
    char e1;
    g.SetTag(v1, VISIT);
    e1 = g.GetElem(v1);
    for (int w = g.FirstAdjVex(v1); w != -1; w = g.NextAdjVex(v1, w))
    {
        if (g.GetTag(w) == UNVISIT)
        {
           
            DFS(g, w, v2,flag);
        }   
    }
    if (flag)
        return 1;
    else
        return 0;

（2）

/*BFSpath.h*/
#include "AdjMatrixDirNetwork.h"
#include"LinkQueue.h"
#include <iostream>
using namespace std;
bool BFSpath(AdjMatrixDirNetwork& g, int v1, int v2) {
    int vexNum = g.GetVexNum();
    if (v1 < 0 || v1 >= vexNum)
    {
        cout << "v1取值不合法!" << endl;
        return 0;
    }
    if (v2 < 0 || v2 >= vexNum)
    {
        cout << "v2取值不合法!" << endl;
        return 0;
    }
    if (v1 == v2)
    {
        cout << "v1与v2不能相等!" << endl;
        return 0;
    }
    for (int v = 0; v < g.GetVexNum(); v++)
        g.SetTag(v, UNVISIT);
    LinkQueue<int> vexq;
    int u, w;
    char e1;
    g.SetTag(v1, VISIT);
    e1=g.GetElem(v1);
    vexq.EnQueue(v1);
    while (!vexq.IsEmpty()) {
        vexq.DelQueue(u);
        for (w = g.FirstAdjVex(u); w != -1; w = g.NextAdjVex(u, w))
            if (g.GetTag(w) == UNVISIT) {
                g.SetTag(w, VISIT);
                e1=g.GetElem(w);
                vexq.EnQueue(w);
                if (e1 == g.GetElem(v2))
                    return 1;
            }
    }
    return 0;
}

（3）

/*ShortestPathDijkstra.h*/
#include "AdjMatrixDirNetwork.h"
#include <iostream>
using namespace std;

void ShortestPathDijkstra(AdjMatrixDirNetwork& network, int startVex)
{
	for (int v = 0; v < network.GetVexNum(); v++)
		network.SetTag(v, UNVISIT);
	int vexNum = network.GetVexNum(), * dist, * path;
	int	i, j, infinity = network.GetInfinity(), min, minOrder;
	dist = new int[vexNum];
	path = new int[vexNum];
	network.SetTag(startVex, VISIT);
	for (i = 0; i < vexNum; i++)    //初始化
	{
		if (i != startVex)
		{
			dist[i] = network.GetWeight(startVex, i);
			if (dist[i] == infinity)
				path[i] = -1;
			else
				path[i] = startVex;
		}
		else
		{
			dist[i] = 0;
			path[i] = -1;
		}
	}
	for (i = 1; i < vexNum; i++)   //循环n-1次，找出以startvex为起点，其他n-1个顶点为终点的最短路径
	{
		min = infinity;
		for (j = 0; j < vexNum; j++)
		{
			if (network.GetTag(j) == UNVISIT && dist[j] < min)
			{
				min = dist[j];
				minOrder = j;
			}
		}
		network.SetTag(minOrder, VISIT);
		for (j = 0; j < vexNum; j++)
		{
			if (network.GetTag(j) == UNVISIT && (min + network.GetWeight(minOrder, j) < dist[j]))
			{
				dist[j] = min + network.GetWeight(minOrder, j);
				path[j] = minOrder;
			}
		}
	}
	for (i = 0; i < vexNum; i++)
	{
		if (i != startVex)
		{
			if (dist[i] != infinity)
			{
				cout << "从起点" << network.GetElem(startVex) << "到终点" << network.GetElem(i) << "的最短路径长度为:" << dist[i];
				cout << "  最短路径为:" << network.GetElem(i);
				j = i;
				while (path[j] != -1)
				{
					j = path[j];
					cout << "<-" << network.GetElem(j);
				}
				cout << endl;
			}
		}
	}
	delete[] dist;
	delete[] path;
}