【算法总结】堆及堆排序总结

【前言】

堆排序是什么？

堆排序的核心是将数组构建成为一个堆，然后从堆顶逐个逐个数字获取，堆分成最大堆（大顶堆）及最小堆（小顶堆）。

下面还是先说明什么是堆。

堆是一颗完全二叉树。---什么是完全二叉树？百度百科--完全二叉树

简而言之，一个二叉树是饱满的---即二叉树都满了，即使没有饱满，那么上一层都是饱满，最后一层叶子节点从左向右排列。

但是堆相对于完全二叉树有了自己的特点，堆分成最大堆及最小堆，

对于最大堆有：

1、根节点（堆顶）的关键字是最大（至少要大于或等于）的；

2、父亲节点必然比左右子节点都要大（至少等于）--左右节点之间没有大小之分，但是都比父亲节点少。

对于最小堆，性质类似：

1、根节点（堆顶）比所有子节点都小或等于；

2、父亲节点比左右子节点都要小或等于。

最大堆及最小堆的插入，删除，构建，取顶操作都类似，不同之处就是父亲比子节点大还是父亲比子节点小。

插入操作的要点

找到合适的节点（假如堆为满二叉树，那么合适的节点为最左侧，假如堆不满，那么合适的节点为倒数第二层的节点【注：这个节点要根据叶子节点决定，假如有倒数第二个节点有一个左子节点，那么该节点就是合适的节点，假如该倒数第二层的节点要么都有左右子节点，要么没有左右子节点，那么选取最接近的没有左右子节点的节点为合适节点】）---合适节点的选取有点麻烦但是您看多几张图片就完全明白为什么这样选取了，找到合适节点后，以合适节点为父节点，添加新节点进去（假如有左子节点，那么就添加为右子节点），添加以后必须上”浮“进行调整（所谓上浮指的是，比较父亲节点，左子节点，右子节点（假如有的话）的关键字，选取最小--或最大--取决于你操作的是最小堆或最大堆----与父亲节点更换然后递归直到根节点，详情可以查看插入操作图解）---说起来复杂，但是各位直接看图解的话会清楚很多。

删除操作的要点

任何删除的节点都是最后面的叶子节点，当前选中的节点恰好是最后面的叶子节点的话，直接删除（不需要调整结构）；假如不是，分两种情况：

A、假如需要删除的节点下面有子节点，那么：先与最后的叶子节点交换关键字，删除最后面的叶子节点，针对需要删除的节点进行下沉操作（”下沉“操作具体看图解），简单来说，对于最小堆的下沉操作是：假如当前节点有子节点，并且父亲节点至少比其中一个子节点要少，那么通过比较与合适的子节点交换关键字，然后以合适的子节点为当前节点递归下沉操作。

B、假如要删除的节点本身就是叶子节点，那么：与最后叶子节点交换关键字，删除最后叶子节点，然后针对需要删除的节点进行上浮操作，简单而言，针对于最小堆，上浮操作就是，假如该节点的关键字小于父亲节点的关键字，那么与父亲节点关键字交换后，以父亲节点作为当前节点继续递归执行上浮操作。

构建堆的要点

计算出最后边的非叶子节点，（通常根据公式节点个数n除以2得出来，大家猜一猜为什么这样计算？），假设该位置为 loc，那么我们接着从 loc到 位置1 或者0（取决于你如何定义根节点的位置）的节点分别进行下沉操作。操作完毕得到的就是堆了。请看图解。

获取堆顶的要点

将堆顶的关键字记录下来，然后根节点（堆顶）的关键字与最后的叶子节点交换，删除最后的叶子节点，然后对根节点进行下沉操作-------看，实际上就是删除根节点的过程。

堆排序的过程就是构建堆及获取堆顶的组合。

对堆的图文介绍

下面我摘抄了   最大堆的插入/删除/调整/排序操作(图解+程序)（JAVA）  的部分内容，图文并茂说明了各种操作：

 堆有最大堆和最小堆之分，最大堆就是每个节点的值都>=其左右孩子（如果有的话）值的完全二叉树。最小堆便是每个节点的值都<=其左右孩子值的完全二叉树。 

  设有n个元素的序列{k1,k2,...,kn},当且仅当满足下列关系时,称之为堆。 
 

堆的三种基本操作(以下以最大堆为例)： 

⑴最大堆的插入   （最小堆类似）

    由于需要维持完全二叉树的形态，需要先将要插入的结点x放在最底层的最右边，插入后满 足完全二叉树的特点； 
  然后把x依次向上调整到合适位置满足堆的性质,例如下图中插入80,先将80放在最后,然后两次上浮到合适位置. 
  时间：O(logn)。  “结点上浮” 
 

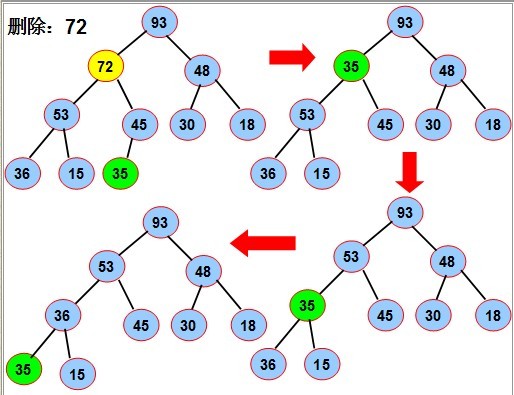
⑵最大堆的删除（最小堆类似） 

   操作原理是：当删除节点的数值时，原来的位置就会出现一个孔,填充这个孔的方法就是， 
把最后的叶子的值赋给该孔并下调到合适位置，最后把该叶子删除。 
  
如图中要删除72,先用堆中最后一个元素来35替换72,再将35下沉到合适位置,最后将叶子节点删除。 
　　 “结点下沉” 

 

【勘误】

大家看到上面的删除过程是不是觉得很容易明白？

我也如此认为，直到我写程序时候出现了问题才重新审视删除算法的正确性。

譬如说：现在有一个最小堆，如下图：

现在我选中了93，并且要删除它，接下来会发生什么事？

接下来就是这个算法的结果了：

对，当节点没有空间下沉的时候它就会无所事事，结果导致不对了。

这种情况下面我们可以借用插入过程的上浮调整方式，从最下面开始向上调整。

⑶堆的初始化---堆得构建 

方法1：插入法： 
  从空堆开始，依次插入每一个结点，直到所有的结点全部插入到堆为止。 
  时间：O(n*log(n)) 
  方法2：调整法： 
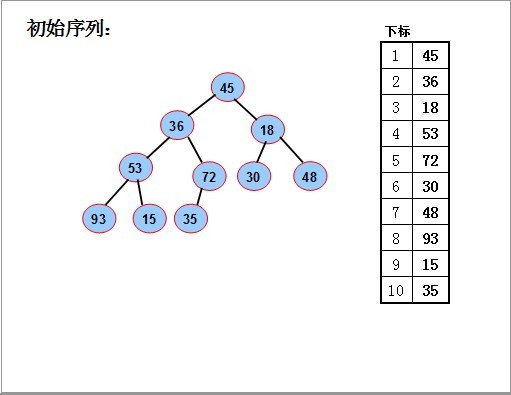
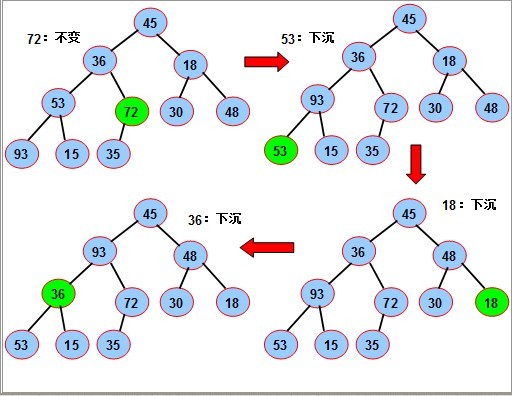
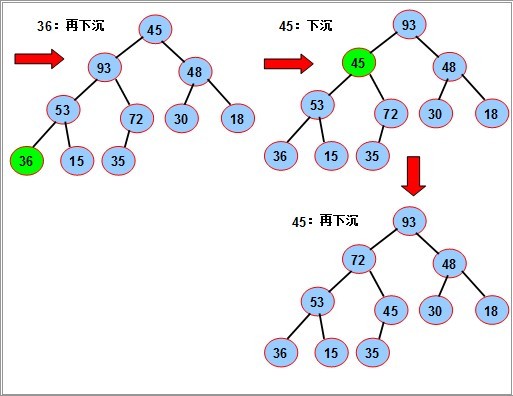
    序列对应一个完全二叉树；从最后一个分支结点（n div 2）开始，到根（1）为止，依次对每个分支结点进行调整（下沉），
以便形成以每个分支结点为根的堆，当最后对树根结点进行调整后，整个树就变成了一个堆。 
  时间：O(n) 
对如图的序列,要使其成为堆,我们从最后一个分支结点(10/2),其值为72开始,依次对每个分支节点53,18,36 45进行调整(下沉). 
 
 
 

【补充说明】

如何获取相应数组序列？

方法是依次将堆的根节点的小数记下，然后删除根节点，如此反复直到堆为空。上面提到了删除操作，每次删除之后都是要调整堆让堆的性质不变，即根节点必为最大值或最小值，明白了吗？

下面将演示堆的相关操作

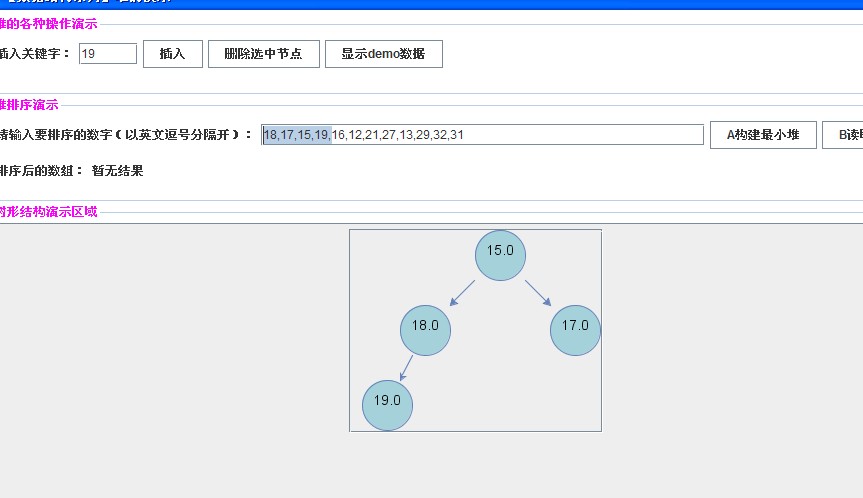
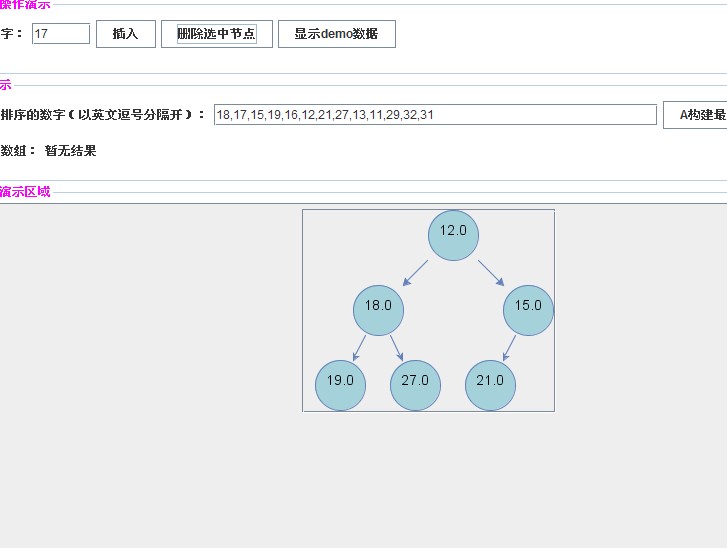
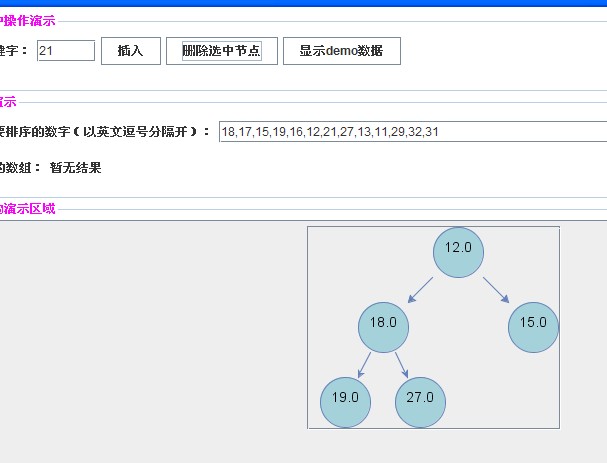
【插入关键字18,17,15,19】

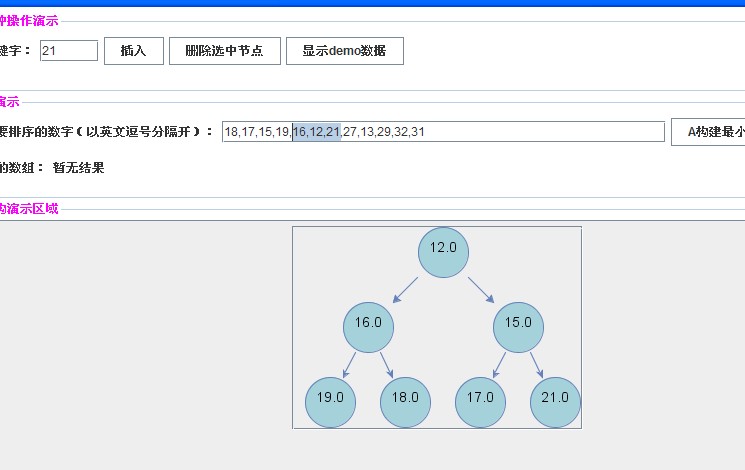
【插入关键字16,12,21】

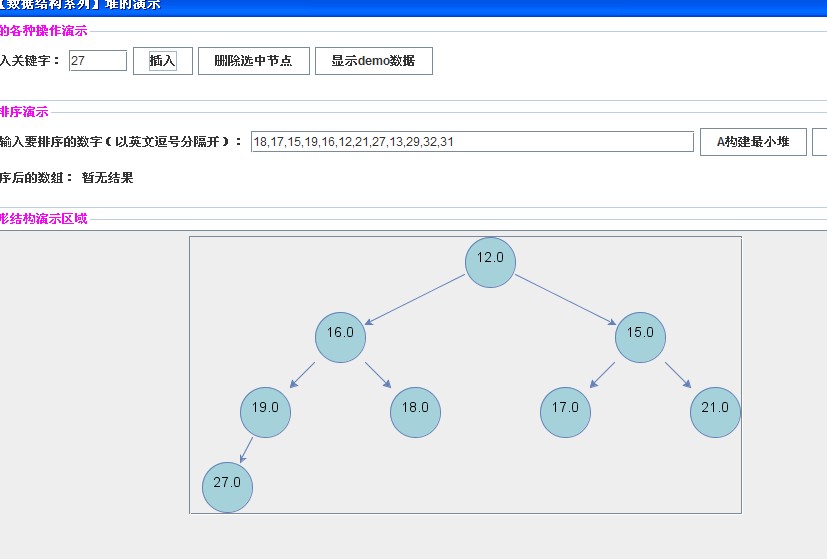
【插入关键字27】

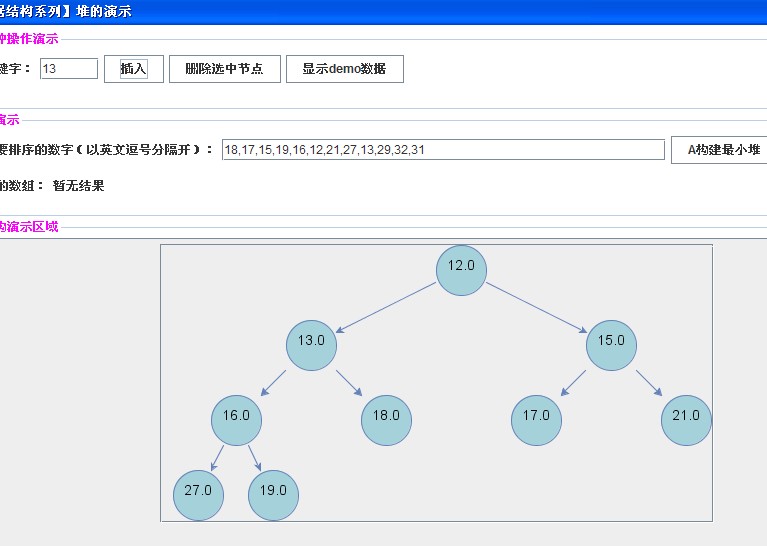
【插入关键字13】

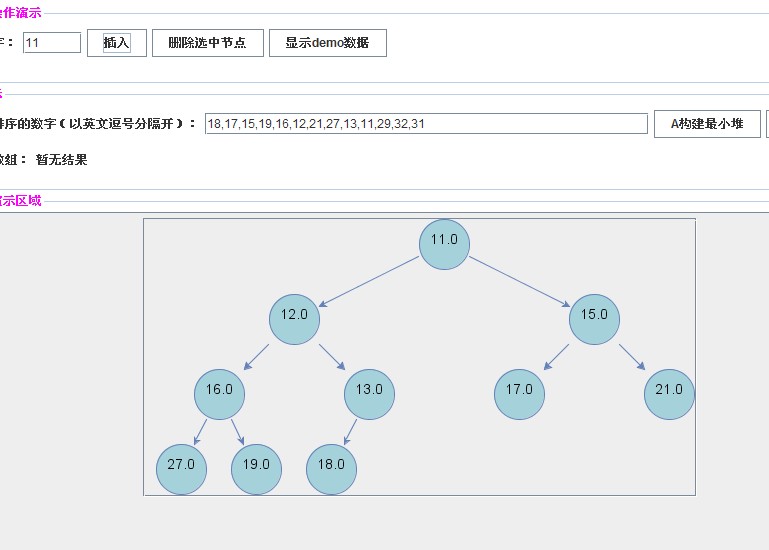
【插入关键字11】

插入操作都大同小异。

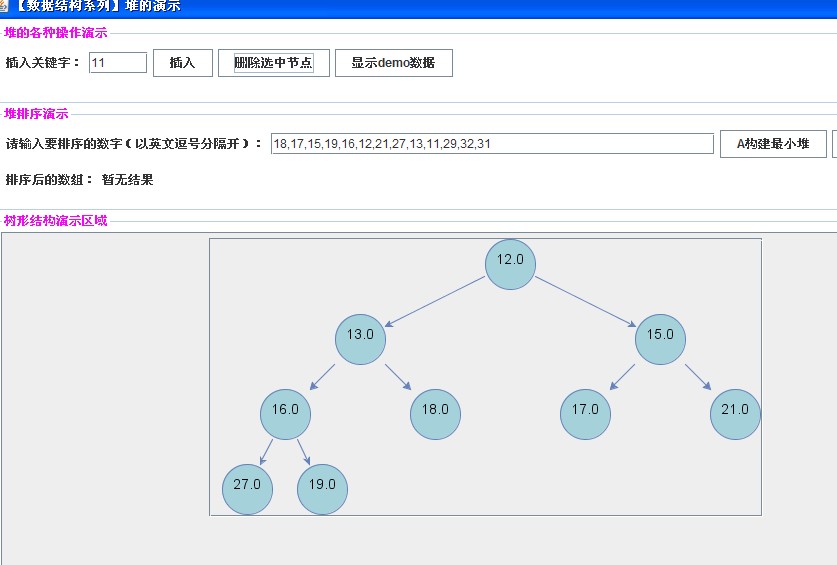
然后进行删除操作：

【删除关键字11】

【删除关键字16】

【删除关键字13】

【删除关键字17】

【删除关键字21】

ok，我们输入数组进去，然后构建一个最小堆：

构建完毕后，我们逐个逐个数读取，形成排序完毕的数组（都从根节点开始读，每读一个根节点就删除一个根节点，调整树形结构，直到空）：

java版核心代码实现

package heap;

public class TreeNode {
public TreeNode parent=null;
public TreeNode leftChild=null;
public TreeNode rightChild=null;
public float key=0.0f;
public TreeNode rightBrother=null;

public TreeNode leftBrother=null;

}

package heap;

import java.util.ArrayList;

import org.apache.velocity.runtime.directive.Break;

/**
 * 最小堆的实现。---
 * 作者：码农下的天桥。
 * 这个是实现最小堆的核心方法，
 * 也是实现堆排序（从小到大）的核心操作类，
 * 它里面有一个TreeNode作为节点的模型类，各位同学在
 * 看完我摘抄的相关文章及勘误后肯定明白是怎么回事。
 * 至于最大堆------------聪明如你们肯定可以举一反三实现出来的。
 * 
 * */

public class MinTopHeap {
	
	private TreeNode _rootNode=null;
	
	private ArrayList<Float> _arrContainer=new ArrayList<Float>();
	
	public void setRootNode(TreeNode rootNode){
		_rootNode=rootNode;
	}
	public TreeNode getRootNode(){
		return _rootNode;
	}



	public boolean insert(float key) {

		/**
		 * 假如当前节点为null，那么可以判断是第一次插入关键字，直接插入。
		 * */
		if(_rootNode==null){
			_rootNode=new TreeNode();
			_rootNode.key=key;
			_arrContainer.add(key);
			return true;
		}
		/**
		 * 假如当前为root根节点，并且没有子节点，那么就插入到根节点的左孩子
		 * */
		if(_rootNode!=null&&_rootNode.leftChild==null&&_rootNode.rightChild==null){
			TreeNode cNode=new TreeNode();
			cNode.key=key;
			cNode.parent=_rootNode;
			_rootNode.leftChild=cNode;
			recursion_adjustment_after_insert(cNode);
			
			return true;
		}
		/**
		 * 假如当前为root节点，并且有左子节点，没有右子节点，那么直接添加右子节点。
		 * */
		if(_rootNode!=null&&_rootNode.leftChild!=null&&_rootNode.rightChild==null){
			TreeNode cNode=new TreeNode();
			cNode.key=key;
			cNode.parent=_rootNode;
			_rootNode.rightChild=cNode;
			
			_rootNode.leftChild.rightBrother=cNode;
			cNode.leftBrother=_rootNode.leftChild;
			recursion_adjustment_after_insert(cNode);
			
			return true;
		}
		/**
		 * 假如这些都不是，那么就判断该树形是不是已经满了，满了的话，直接在最左边添加一个左子节点，
		 * 否则，找出最后的那一个叶子节点，然后判断并添加一个节点。
		 * */
		
		TreeNode cNode=getSuitableNode();
		String t1="";
		System.out.print(t1);
		if(cNode==null){
			return false;
		}
		TreeNode realNode=new TreeNode();
		realNode.key=key;
		if(cNode.leftChild==null){
			cNode.leftChild=realNode;
			realNode.parent=cNode;
			//--请注意，需要检查是否有左边的靠近这边的兄弟，有的话需要修改指针。
			if(cNode.parent!=null){
			
				TreeNode leftAncle=cNode.leftBrother;
				
				if(leftAncle!=null){
					leftAncle.rightChild.rightBrother=realNode;
					realNode.leftBrother=leftAncle.rightChild;					
				}
				
				
			}
			recursion_adjustment_after_insert(realNode);
			
			return true;
		}
		else if(cNode.rightChild==null){
			cNode.rightChild=realNode;
			realNode.parent=cNode;
			cNode.leftChild.rightBrother=realNode;
			realNode.leftBrother=cNode.leftChild;
			recursion_adjustment_after_insert(realNode);
			return true;
		}
		
		
		// TODO Auto-generated method stub
		return false;
	}
	private TreeNode ___suitableNode=null;
	
	public boolean delete(float key){
		TreeNode lastNode=getLastNode();
		if(lastNode==null){
			return false;
		}
		if(_rootNode==null){
			return false;
		}
		TreeNode deletedNode=getNode(key);

		if(deletedNode==null){
			return false;
		}
		
	
		
		TreeNode lastParent=lastNode.parent;
		
		
		if(lastParent!=null){
			boolean isLeft=true;
			if(lastParent.rightChild!=null&&lastParent.rightChild.key==lastNode.key){
				isLeft=false;
			}
			if(isLeft==true){
				lastParent.leftChild=null;
				if(lastParent.leftBrother!=null){
					lastParent.leftBrother.rightChild.rightBrother=null;
				}
			}else{
				lastParent.rightChild=null;
				lastParent.leftChild.rightBrother=null;
			}
			/**
			 * 注意，假如删除的节点没有左右子节点，并且它与最后的真实删除的节点并非同一个，那么就必须上浮调整各个节点的位置了。
			 * */
			if(deletedNode.leftChild==null&&deletedNode.rightChild==null&&deletedNode.key!=lastNode.key){
				deletedNode.key=lastNode.key;
		     	recursion_adjustment_after_insert(deletedNode);
				return true;
			}
/**
 * 假如需要删除的节点跟最后节点是一样的，那么我们可以认为这个节点就是最后的节点。那么直接删除就好了。
 * */
			else if(deletedNode.key==lastNode.key){
				
				return true;
			}
			else{
				deletedNode.key=lastNode.key;
				recursion_adjustment_after_deletion(deletedNode);
				return true;
			}
		}
		else{
		_rootNode=new TreeNode();	
		return true;
		}
		
	}
	
	private TreeNode getSuitableNode(){
		if(_rootNode==null){
			return null;
		}
		if(_rootNode.leftChild==null){
			return _rootNode;
		}
		
		/**
		 * 查看最左侧节点。
		 * */
		TreeNode preNode=null;
		TreeNode cNode=_rootNode;
		int theHeight=1;
		while(cNode.leftChild!=null){
			theHeight++;
			cNode=cNode.leftChild;
		}
		int lvMaxNodes=(int)Math.pow(2.0, (double)(theHeight-1));
		int lvRealNodes=1;
		TreeNode lvLastNode=cNode;
		while (lvLastNode.rightBrother!=null) {
			lvRealNodes++;
			lvLastNode=lvLastNode.rightBrother;
			
		}
		
		//判断当前节点所在层数的节点数量是否已经满了。
		if(lvRealNodes<lvMaxNodes){
			boolean isLeft=true;
			TreeNode parentNode=lvLastNode.parent;
			
			if(parentNode.rightChild!=null&&parentNode.rightChild.key==lvLastNode.key){
				isLeft=false;
			}
			else if(parentNode.leftChild!=null&&parentNode.leftChild.key==lvLastNode.key){
				isLeft=true;
			}
			if(isLeft==true){
				return parentNode;
			}
			else{
				if(parentNode.rightBrother==null){
					return cNode;
				}
				else{
					return parentNode.rightBrother;
				}
			}
		}
		else{
			
			return cNode;
		}
				
		
		
	}



	public boolean pop() {
		// TODO Auto-generated method stub
		return false;
	}

	public boolean containsKey(float key) {
		// TODO Auto-generated method stub
		___containsKey=false;
		recursion_search_key(_rootNode, key);
		
		return ___containsKey;
	}
	private boolean ___containsKey=false;
	private void recursion_search_key(TreeNode node,float key){
		if(node==null){
			return;
		}
		if(node.key==key){
			___containsKey=true;
			return;
		}
		recursion_search_key(node.leftChild, key);
		recursion_search_key(node.rightChild, key);
	}
	
	private TreeNode ___searchNode=null;
	public TreeNode getNode(float key){
		___searchNode=null;
		recursion_search_node(_rootNode, key);
		return ___searchNode;
	}
	
	private void recursion_search_node(TreeNode currentNode,float key){
		if(currentNode==null){
			return;
		}
		if(currentNode.key==key){
			___searchNode=currentNode;
			return;
		}
		else{
			recursion_search_node(currentNode.leftChild, key);
			recursion_search_node(currentNode.rightChild, key);
		}
	}
	
	/**
	 * 请注意，simpleinsert这个方法只是单纯将关键字插入到二叉树里面，
	 * 每次查完它都不会主动调整使其成为一个最小堆，为什么要有这个方法呢？
	 * 因为每个需要排序的数组往往有多个数字，假如每次插入都调整那么就很麻烦了，
	 * 倒不如插入以后，一次性调整。
	 * 
	 * */
	private boolean simpleInsert(float key){
		/**
		 * 假如当前节点为null，那么可以判断是第一次插入关键字，直接插入。
		 * */
		if(_rootNode==null){
			_rootNode=new TreeNode();
			_rootNode.key=key;
			_arrContainer.add(key);
			return true;
		}
		/**
		 * 假如当前为root根节点，并且没有子节点，那么就插入到根节点的左孩子
		 * */
		if(_rootNode!=null&&_rootNode.leftChild==null&&_rootNode.rightChild==null){
			TreeNode cNode=new TreeNode();
			cNode.key=key;
			cNode.parent=_rootNode;
			_rootNode.leftChild=cNode;
			//recursion_adjustment_after_insert(cNode);
			
			return true;
		}
		/**
		 * 假如当前为root节点，并且有左子节点，没有右子节点，那么直接添加右子节点。
		 * */
		if(_rootNode!=null&&_rootNode.leftChild!=null&&_rootNode.rightChild==null){
			TreeNode cNode=new TreeNode();
			cNode.key=key;
			cNode.parent=_rootNode;
			_rootNode.rightChild=cNode;
			
			_rootNode.leftChild.rightBrother=cNode;
			cNode.leftBrother=_rootNode.leftChild;
			//recursion_adjustment_after_insert(cNode);
			
			return true;
		}
		/**
		 * 假如这些都不是，那么就判断该树形是不是已经满了，满了的话，直接在最左边添加一个左子节点，
		 * 否则，找出最后的那一个叶子节点，然后判断并添加一个节点。
		 * */
		
		TreeNode cNode=getSuitableNode();
		String t1="";
		System.out.print(t1);
		if(cNode==null){
			return false;
		}
		TreeNode realNode=new TreeNode();
		realNode.key=key;
		if(cNode.leftChild==null){
			cNode.leftChild=realNode;
			realNode.parent=cNode;
			//--请注意，需要检查是否有左边的靠近这边的兄弟，有的话需要修改指针。
			if(cNode.parent!=null){
			
				TreeNode leftAncle=cNode.leftBrother;
				
				if(leftAncle!=null){
					leftAncle.rightChild.rightBrother=realNode;
					realNode.leftBrother=leftAncle.rightChild;					
				}
				
				
			}
			recursion_adjustment_after_insert(realNode);
			
			return true;
		}
		else if(cNode.rightChild==null){
			cNode.rightChild=realNode;
			realNode.parent=cNode;
			cNode.leftChild.rightBrother=realNode;
			realNode.leftBrother=cNode.leftChild;
			//recursion_adjustment_after_insert(realNode);
			return true;
		}
		
		
		// TODO Auto-generated method stub
		return false;		
	}
	
private void recursion_adjustment_after_insert(TreeNode _node){
	if(_node==null){
		return;
	}
	TreeNode parentNode=_node.parent;
	if(parentNode==null){
		return;
	}
	if(_node.key<parentNode.key){
		float tmp1=parentNode.key;
		parentNode.key=_node.key;
		_node.key=tmp1;
		recursion_adjustment_after_insert(parentNode);
		return;
		
	}
	else{
		return;
	}
}

private void recursion_adjustment_in_inition(TreeNode currentNode){
	if(currentNode==null){
		return;
	}
	if(currentNode.leftChild==null){
		return;
	}
	TreeNode leftChild=currentNode.leftChild;
	TreeNode rightChild=currentNode.rightChild;
	float tmpKey=currentNode.key;
	if(leftChild!=null&&rightChild!=null){
		if(leftChild.key<currentNode.key&&rightChild.key<currentNode.key){
			
			if(leftChild.key<=rightChild.key){
				currentNode.key=leftChild.key;
				leftChild.key=tmpKey;
				
				recursion_adjustment_in_inition(leftChild);
				return;
			}
			else{
				currentNode.key=rightChild.key;
				rightChild.key=tmpKey;
				recursion_adjustment_in_inition(rightChild);
				return;
			}
		}
		else if(leftChild.key<currentNode.key&&rightChild.key>=currentNode.key){
			currentNode.key=leftChild.key;
			leftChild.key=tmpKey;
			
			recursion_adjustment_in_inition(leftChild);
			return;
		}
		else if(leftChild.key>=currentNode.key&&rightChild.key<currentNode.key){
			currentNode.key=rightChild.key;
			rightChild.key=tmpKey;
			recursion_adjustment_in_inition(rightChild);
			return;
		}
		else{
			return;
		}
	}
	else if(leftChild!=null&&rightChild==null){
		if(leftChild.key<currentNode.key){
			currentNode.key=leftChild.key;
			leftChild.key=tmpKey;
			
			recursion_adjustment_in_inition(leftChild);
			return;
		}		
		else{
			return;
		}
	}
	else{
		return;
	}
}

/**
 * 当前节点被删除后，下沉过程调整。
 * */
private void recursion_adjustment_after_deletion(TreeNode currentNode){
	if(currentNode==null){
		return;
	}
	float ftmp=currentNode.key;
	if(currentNode.leftChild==null&¤tNode.rightChild==null){
		return;
	}
	if(currentNode.leftChild!=null&¤tNode.rightChild!=null){
		if(currentNode.leftChild.key<currentNode.key&¤tNode.rightChild.key<currentNode.key){
			if(currentNode.leftChild.key<=currentNode.rightChild.key){
				currentNode.key=currentNode.leftChild.key;
				currentNode.leftChild.key=ftmp;
				
				recursion_adjustment_after_deletion(currentNode.leftChild);
				return;
			}
			else{
				currentNode.key=currentNode.rightChild.key;
				currentNode.rightChild.key=ftmp;
				recursion_adjustment_after_deletion(currentNode.rightChild);
				return;
				
			}
		}
		else if(currentNode.leftChild.key<currentNode.key){
			currentNode.key=currentNode.leftChild.key;
			currentNode.leftChild.key=ftmp;
			recursion_adjustment_after_deletion(currentNode.leftChild);
			return;
			
		}
		else if(currentNode.rightChild.key<currentNode.key){
			currentNode.key=currentNode.rightChild.key;
			currentNode.rightChild.key=ftmp;
			recursion_adjustment_after_deletion(currentNode.rightChild);
			return;
		}
		else{
			return;
		}
	}
	else if(currentNode.leftChild!=null&¤tNode.rightChild==null){
		 if(currentNode.leftChild.key<currentNode.key){
				currentNode.key=currentNode.leftChild.key;
				currentNode.leftChild.key=ftmp;
				recursion_adjustment_after_deletion(currentNode.leftChild);
				return;
				
			}
		 return;
	}
	else{
		return;
	}
	
}

private TreeNode getLastNode(){
	if(_rootNode==null){
		return null;
	}
	TreeNode cNode=_rootNode;
	while(cNode.leftChild!=null){
		cNode=cNode.leftChild;
	}
	TreeNode lvLastNode=cNode;
	while(lvLastNode.rightBrother!=null){
		lvLastNode=lvLastNode.rightBrother;
	}
	return lvLastNode;
}
/**
 * 根据index来获得节点，请注意，index从零开始。
 * */
public TreeNode getTreeNodeByIndex(int loc){
	if(_rootNode==null){
		return null;
	}
	if(loc<=-1){
		return null;
	}
	int cindex=0;
	if(loc==0){
		return _rootNode;
	}else{
		int theHeight=1;
		TreeNode leftNode=_rootNode;
		
		while(leftNode.leftChild!=null){
			leftNode=leftNode.leftChild;
			theHeight++;
		}
		int cHeight=1;
		TreeNode resultNode=null;
		TreeNode lvFirstNode=_rootNode;
		
		TreeNode tmpRightNode=null;
		
		
		for(cindex=0;cindex<=loc;cindex++){
			if(cHeight>theHeight){
				break;
			}
		    if(lvFirstNode==null){
		    	break;
		    }	
		    
		    
		    if(loc==0){
		    	return _rootNode;
		    }
		    
		    tmpRightNode=lvFirstNode;
		    
		    while(tmpRightNode!=null){
		    	if(cindex==loc){
		    		return tmpRightNode;
		    	}
		    	tmpRightNode=tmpRightNode.rightBrother;
		    	if(tmpRightNode==null){
		    		break;
		    	}
		    	else{
		    		cindex++;	
		    	}
		    	
		    }
			
			
			
			lvFirstNode=lvFirstNode.leftChild;
	        cHeight++;
		}
		
		return resultNode;
	}
	
}
public void fromArray_origin(float[] arr){
	_rootNode=null;
	if(arr==null){
		return;
	}
	else{
		for(float f1:arr){
			simpleInsert(f1);
		}
	}
	int theLength=arr.length;
	int middle_loc=(int)Math.floor((double)((double)theLength/2.0))-1;
	if(theLength<=1){
		return ;
	}
	//--循环进行上浮调整。
}
/**
 * 将原始数组构建成为完全二叉树，再调整成为最小堆，然后
 * 返回堆的根节点。
 * 请注意查看我摘抄的图文教程，主要就是从最后一个不为叶子节点的节点开始，
 * 通过比较进行下沉，直到根节点结束。
 * 当然，假如您的节点数据里面没有leftBrother之类的指针你会发现按照排位寻找节点是如此麻烦。
 * */

public TreeNode fromArray(float[] arr){
	_rootNode=null;
	if(arr==null){
		return null;
	}
	else{
		for(float f1:arr){
			simpleInsert(f1);
		}
	}
	int theLength=arr.length;
	int middle_loc=(int)Math.floor((double)((double)theLength/2.0))-1;
	System.out.println("最下面的非叶子节点：【"+middle_loc+"】");
	if(theLength<=1){
		return _rootNode;
	}
	//--循环进行上浮调整。
	for(int i=middle_loc;i>=0;i--){
		TreeNode cNode=getTreeNodeByIndex(i);
		recursion_adjustment_in_inition(cNode);
		
	}
	
	return _rootNode;
}
/**
 * 通过根节点来逐个读取数字，然后组成从小到大的数组。
 * */
public ArrayList<Float> toArray(){
	
	
	
	
	if(_rootNode==null){
		return null;
	}
	
	ArrayList<Float> _arr=new ArrayList<Float>();
	while(_rootNode!=null){
		_arr.add(_rootNode.key);
		deleteNode(_rootNode);
	}
	

	
	
	return _arr;
}


public boolean deleteNode(TreeNode currentNode){
	TreeNode lastNode=getLastNode();

	TreeNode deletedNode=currentNode;

	if(deletedNode==null){
		return false;
	}
	
	/**
	 * 假如只有一个根节点，没有子节点的话，那么就直接删除
	 * */
 if(currentNode!=null&¤tNode.parent==null&¤tNode.leftChild==null&¤tNode.rightChild==null){
	 _rootNode=null;
	 currentNode=null;
	 return true;
 }	
	

	
	TreeNode lastParent=lastNode.parent;
	
	
	if(lastParent!=null){
		boolean isLeft=true;
		if(lastParent.rightChild!=null&&lastParent.rightChild.key==lastNode.key){
			isLeft=false;
		}
		if(isLeft==true){
			lastParent.leftChild=null;
			if(lastParent.leftBrother!=null){
				lastParent.leftBrother.rightChild.rightBrother=null;
			}
		}else{
			lastParent.rightChild=null;
			lastParent.leftChild.rightBrother=null;
		}
		/**
		 * 注意，假如删除的节点没有左右子节点，并且它与最后的真实删除的节点并非同一个，那么就必须上浮调整各个节点的位置了。
		 * */
		if(deletedNode.leftChild==null&&deletedNode.rightChild==null&&deletedNode.key!=lastNode.key){
			deletedNode.key=lastNode.key;
	     	recursion_adjustment_after_insert(deletedNode);
			return true;
		}
/**
* 假如需要删除的节点跟最后节点是一样的，那么我们可以认为这个节点就是最后的节点。那么直接删除就好了。
* */
		else if(deletedNode.key==lastNode.key){
			
			return true;
		}
		else{
			deletedNode.key=lastNode.key;
			recursion_adjustment_after_deletion(deletedNode);
			return true;
		}
	}
	else{
	_rootNode=new TreeNode();	
	return true;
	}
	
}


}

演示程序及资源

演示程序

假如这篇文章对您有所帮助，我会感到很荣幸。