生命起源和人工生命研究模型的调节发育-CSDN博客

来源：CreateAMind

Regulative development as a model for origin of life and artificial life studies

生命起源和人工生命研究模型的调节发育

https://doi.org/10.1016/j.biosystems.2023.104927

摘要：
利用自由能原理的形式框架，我们展示了系统与环境之间双向信息交换的通用热力学要求如何产生复杂性。这导致在远离热平衡的系统中出现了分层计算架构。在这种情况下，任何系统的环境通过“工程化”系统以增加其形态复杂性，从而提高对系统行为的预测能力，进而产生更大规模、更宏观的行为。从这个角度来看，调节发育成为一种环境驱动的过程，其中“部件”被组装以产生具有可预测行为的系统。基于此，我们认为生命在热力学上是有利的，而人类工程师在设计人工生命系统时，类似于一个通用的“环境”。

关键词：自由能原理；运动复制；学习；多细胞性；多尺度能力架构；目标形态

1. 引言

生物系统是组件的分层排列，这些组件表现出多尺度能力架构（Multiscale Competency Architecture, MCA；Levin, 2022; Clawson 和 Levin, 2022）。在 MCA 中，每个尺度上的组件都能够独立执行该尺度上适当的功能，而无需明确的自上而下的指令。例如，人类细胞不需要大脑或任何更大尺度的系统告知其如何分裂；它们自身就具备分裂的能力。在 MCA 的任何尺度 j 上，下一层级 j−1 的组件行为为 j 适当的行为提供了使能机制，而上一层级 j+1 的组件行为则施加了边界条件。由于边界条件有效限制了尺度 j 上的可能性空间，因此尺度 j+1 上的状态变化可以调节或变形尺度 j 上的可能性空间，从而提供自上而下的新奇性来源。例如，细胞分裂由细胞内的基因表达使能，同时受到周围多细胞组织的信号传导或传递的限制。来自周围甚至远端（McMillan 等，2021）组织的自上而下的“指令”可以增加或减少细胞分裂的速率，例如在伤口愈合期间；其他例子包括微环境对癌细胞特性的调节（Bissell, 2002; Ingber, 2008; Bizzarri 和 Cucina, 2014）、再生过程中大尺度轴向模式线索对干细胞命运的调控（Durant 等，2017），以及基于其更大解剖学背景对结构的局部重塑（Farinella-Ferruzza, 1956）。Polanyi（1968）、Rosen（1986）、Pezzulo 和 Levin（2016）以及 Fields 和 Levin（2020a）等人都将这种使能机制的向上流动和约束边界条件的向下流动识别为生物系统的特征。用认知科学或计算机科学的语言来说，MCA 封装了在适当尺度上执行适当行为所需的能力。这种能力的封装使得每个尺度上特定的过程能够作为虚拟机（Smith 和 Nair, 2005）独立于较低或较高尺度组件的实现而运行。这种实现独立性为“混合和匹配”系统开辟了可能性，这些系统可以几乎任意地结合进化生物、工程生物和人工组件（Levin, 2022; Clawson 和 Levin, 2022）。

要精确地阐述 MCA 的概念，需要对“能力”有一个精确的定义。变分自由能原理（Variational Free Energy Principle, FEP）提供了一个完全精确的定义：系统“有能力”到它最小化其环境的变分自由能（Variational Free Energy, VFE）的程度，该自由能是在马尔可夫毯（Markov Blanket, MB）上测量的，马尔可夫毯在统计上将其与环境分开（即使其状态与环境的状态条件独立）。系统测量的 VFE 是意外性的上界，因此也是其环境对其 MB 的行为的不可预测性的上界。作为一种建模框架，FEP 对于具有明确定义的状态空间且其状态与环境状态条件独立的物理系统具有可证明的普适性，即具有马尔可夫毯的系统。自其作为大脑功能理论被引入（Friston, 2005; Friston, Kilner 和 Harrison, 2006; Friston, 2010）以来，FEP 已发展成为生物系统的一般理论（Friston, 2013; Friston 等，2017; Ramstead, Badcock 和 Friston, 2018; Ramstead 等，2019; Kuchling 等，2020），并最近被表述为经典（Friston, 2019; Ramstead 等，2022）和量子（Fields 等，2022）物理系统的一般理论。这种普适性的关键在于 FEP 并未指定系统如何最小化其检测到的 VFE，这与“能力”的一般观念一致，即“能力”不仅涉及解决问题的能力，还涉及在不同情境中以不同方式或通过不同手段解决相同问题的能力。最小化 VFE 就是最大化其通过 MB 对环境的未来行为的可预测性，这种有效行为在 FEP 文献中被称为“主动推断”。因此，“有能力”的系统是通过其对环境的行为来增加其未来预测能力的系统。正如下面更详细讨论的那样，维持稳态/适应性行为是这种有效行为的例子，探索性行为也是如此，这些行为能够获取有用的信息。

通过提供一个无尺度的、热力学上的能力定义，自由能原理（FEP）使得生物学能够摆脱尺度限制，将进化和发育视为一个单一过程——变分自由能（VFE）最小化——在不同组织层次上的表现（Fields 和 Levin，2020a；b）。将这种“生物学”的概念扩展到涵盖与生物学相关的前生物、非生物或外星生物情景是顺理成章的。在这里，我们提出发育和再生——这些调节形态发生过程使得多细胞系统能够在显著的干扰或改变起始条件下达到“正常”的目标形态（Birnbaum 和 Alvarado，2008；Levin，2011；Vandenberg、Adams 和 Levin，2012；Lobo、Solano、Bubenik 和 Levin，2014；Pezzulo 和 Levin，2016；Pinet 和 McLaughlin，2019；Fields 和 Levin，2020b）——为生命起源和人工生命研究提供了一个模型。

在这里，我们使用 FEP 提供的“能力”定义，研究无尺度生物学解释的一个特定实例。考虑两个生物自组织的例子：

调节发育：利用周围环境提供的信息，一定数量的细胞自组织成一个多细胞生物。结果也可能是像微生物席这样的兼性多细胞系统。
从头自组织：一定数量的分子自组织成一个细胞。结果也可能是某些生命起源模型中的自维持原细胞。

调节发育已经被研究了两个多世纪，许多模型系统现在在细节上得到了相当程度的理解，包括在某些情况下，细胞特异性的基因表达谱（Tintori 等，2016；Farnsworth、Saunders 和 Miller，2020；Wang 等，2022）。另一方面，从头自组织的例子仍然是假设性的。尽管在生命起源的背景下提出了各种模型，但没有一个被完全实验证实，甚至关于它们的生物学合理性也几乎没有共识。任何无尺度解释的目标是讲述关于这两个例子完全相同的故事。通过要求从头自组织的例子成为调节发育的形式和机械类比来构建这样的解释，引发了一系列问题，这些问题主要涉及从头自组织中“环境”的结构和作用，这些问题相对被以往的方法所忽视。

我们将看到，特别是，将从头自组织视为调节发育的类比，挑战了两个根深蒂固的观点。首先，它质疑了几乎普遍的假设，即任何从头模型都必须导致一个自我复制的系统。从达尔文开始的进化模型强烈地将变异与通过繁殖的遗传联系在一起（Monod，1972；Szathmáry 和 Maynard Smith，1995；Michod，1999）。自然选择作用于变体，因此在达尔文模型中依赖于繁殖。这些模型暗示了涉及自我复制分子的从头过程。我们将提出，那些由环境过程生成所需“部件”的模型也值得考虑，这些环境过程与感兴趣的系统最多只有弱耦合。由弱耦合过程产生的变异与全球尺度上的进化是一致的，但并不依赖于任何单一局部尺度上的自然选择；因此，它提供了一种“非达尔文式”的秩序来源。这种弱耦合在涉及包含工程和制造组件的自组织系统的情况中得到了体现；我们建议弱耦合模型在其他环境中也可能是现实的。

其次，将从头自组织视为调节发育的类比，挑战了自组织的概念本身。在其最纯粹的形式中，自组织的概念暗示组织所需的信息存在于自我之中。这立即提出了一个本质上无法回答的问题：这些关键信息最初是如何到达那里的。直接将从头自组织与调节发育联系起来，迫使我们在过程的每一步都问，哪些系统算作“自我”，每个“自我”的环境是如何定义的，以及在每种情况下，“自我”与环境之间的信息交换是如何实现的（Levin，2021）。

我们的分析得出了两个广泛的结论：

繁殖是一种效率提升手段，进化通过在细菌中选择强大的自我/他者识别系统将其“固化”。将复制与自组织解耦，将研究对象推广到发育研究中的“平等主义”（Strassmann 和 Queller，2010）的组件集合，这些组件无关或在进化情况下只有远亲关系，但“恰好”能够很好地协同工作。这使得生命起源的故事更加简单。它承认了生物系统中运动复制的可能性，正如在由非洲爪蟾皮肤细胞构建的“异形机器人”中实验观察到的那样（Kriegman, Blackiston, Levin 和 Bongard，2021）。它表明，微生物席这样的共生系统至少与严格有性生殖的多细胞生物一样“典型”。在这种情况下，从头和发育研究的重点都变成了，一旦组件被放置在相互邻近的位置，它们如何相互作用，而不管它们的起源如何。

2. “自组织”总是依赖于环境的，因此我们可以将其视为至少部分是由环境引导的：一些指导性信息最初在环境中，而不是在组装的自我中。从物理相互作用（Fields 和 Marcianò，2020；Fields, Glazebrook 和 Marcianò，2021）或自由能原理（FEP）（Friston，2019；Ramstead 等，2022；Fields, Friston, Glazebrook 和 Levin，2022）的角度来看，这是显而易见的。在许多生命起源模型、微生物席组装和胚胎发生中，甚至在像秀丽隐杆线虫这样的“欧洲计划”生物中（Barrière 和 Bertrand，2020），这也是显而易见的。尽管如此，它通常被忽视或被淡化，特别是在理论工作中。

在接下来的内容中，我们首先在第 2 节中从 Fields, Friston, Glazebrook 和 Levin（2022）所采用的一般视角出发，描述任何系统与其环境之间的相互作用。原则上，任何这样的相互作用在信息上是对称的——信息在两个方向上流动的量是相等的——但双方如何使用它们接收到的信息可能截然不同。换句话说，对称的信息流与系统-环境边界两侧“认知光锥”（Levin，2021；2022）的不同宽度和深度是一致的，因此也与不同的主动推断能力是一致的。我们在第 3 节转向对调节发育和从头自组织的明确比较，首先描述每个活跃组件的环境作为信息源，因此作为它们自身的活跃主体，在过程的每一步中。我们特别研究了调节发育和从头自组织如何减少环境检测到的 VFE，因此是在 FEP 下由热力学驱动的过程。我们在第 4 节考虑发育中的“自我”如何表示自己，以及这个过程如何依赖于记忆和计算资源。我们展示了自我表示作为数据结构的复杂性与系统的认知光锥体积成比例，并讨论了在维护这种数据结构和进行主动推断之间在能量和记忆资源方面的权衡。我们在第 5 节区分了被动训练和主动学习，并指出信息对称性如何使所有现实情况成为两者的混合。最后，我们在第 6 节概述了一种由这些结果建议的“混合和匹配”实验策略。

2. 信息对称性与认知不对称性一致

2.1 物理相互作用的信息对称性

自由能原理（FEP）适用于所有能够与环境在宏观时间尺度上区分开来的系统，无论是经典系统还是量子系统。这里的“环境”指的是除了感兴趣系统之外的一切。系统与环境的可区分性或分离性要求在联合系统-环境状态空间中存在一个边界，以确保系统状态与环境状态之间的条件统计独立性（从而零纠缠熵）。这个边界作为马尔可夫毯（MB），它可以由空间边界（如细胞膜）实现，但并非必须。系统-环境相互作用正是在这个边界上定义的。这种相互作用的（二进制）维度是其最大特征值的最小长度二进制编码中的位数 N。相互作用的维度 N 也是边界状态空间的维度；事实上，任何这样的边界都可以表示为 N个量子比特的数组。因此，系统-环境相互作用总是可以被视为在系统和环境之间双向传输 N 位信息；这些 N 位信息在任何微观（相对于相互作用的特征时间）时间间隔 dt 内，指定了该时间间隔内的相互作用特征值。换句话说，所有物理相互作用在信息上都是对称的；不存在单向的信息流。

信息和热力学能量可以通过兰道尔原理想互转换，并且直接的信息到能量的转换已经在实验中得到证实。因此，任何传递信息的物理相互作用都会传递热力学能量。处理信息以获得对后续行为有影响的答案，即不可逆的经典计算，根据兰道尔原理，都有有限的自由能成本。因此，任何利用环境中的信息来改变其行为的系统——显然包括任何生物系统——都必须将从环境中获得的一部分信息/能量用于经典计算的自由能成本。因此，从环境中获得的能量量为系统可以执行的经典计算量（每单位时间的比特数）提供了严格的上限。因此，我们可以将任何系统-环境相互作用表示为在边界上双向交换信息，其中每一方都将一部分信息用于经典计算的自由能需求，如图 1 所示。

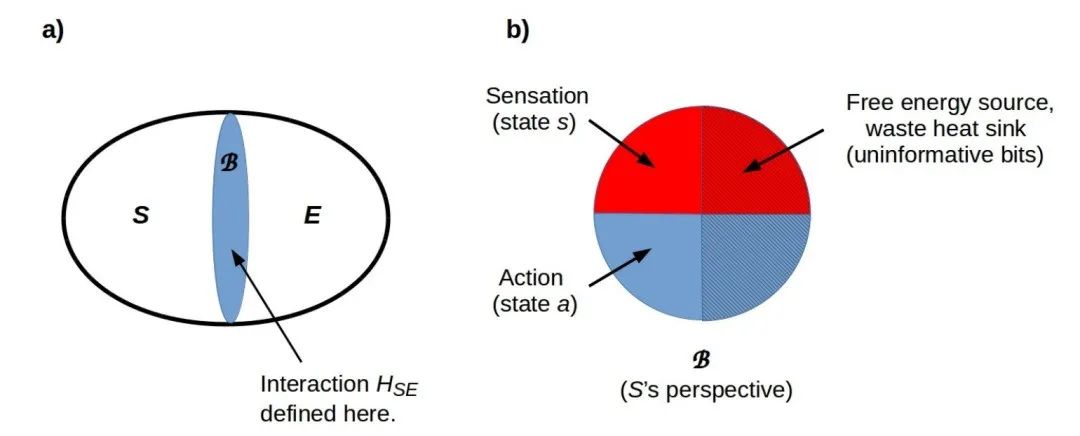
物理相互作用的信息对称性在自由能原理（FEP）背景下有一个重要的推论：任何系统 S 的环境 E 必须被视为一个主体。FEP 要求这个主体 E 进行主动推断，即它对它的环境——感兴趣的系统 S——采取行动，以最小化它 E 在其马尔可夫毯（MB）上测量到的变分自由能（VFE）。由于每个系统的马尔可夫毯仅仅是它们之间的（状态空间）边界，FEP 要求任何一对相互作用的系统以一种方式行事，使得它们都在它们共同的边界上最小化它们测量到的 VFE。在 S-E 相互作用纯粹是热力学的情况下，即 S 和 E 都不进行任何经典计算，它们通过接近热力学平衡来最小化测量到的 VFE。如果 S 或 E 中的任何一个进行经典计算，最小化 VFE 的解通常不在热力学平衡中，而是 S 和 E 的非平衡稳态（NESS）解（关于详细信息，请参阅 Friston, 2019）。这样的解从两个组成部分系统的角度来看都遵守第二定律：S 和 E 各自从它们的相互作用伙伴吸收自由能，并向其排放废热，即 E 和 S 分别。因此，每个系统都“看到”其相互作用伙伴的熵增加。总系统 SE 的熵是其总信息量，这是严格守恒的，因此可以重新调整为零（关于在这个双部分解设置中的熵的讨论，请参阅 Tegmark, 2012）。

2.2 信息对称性与热力学不对称性一致

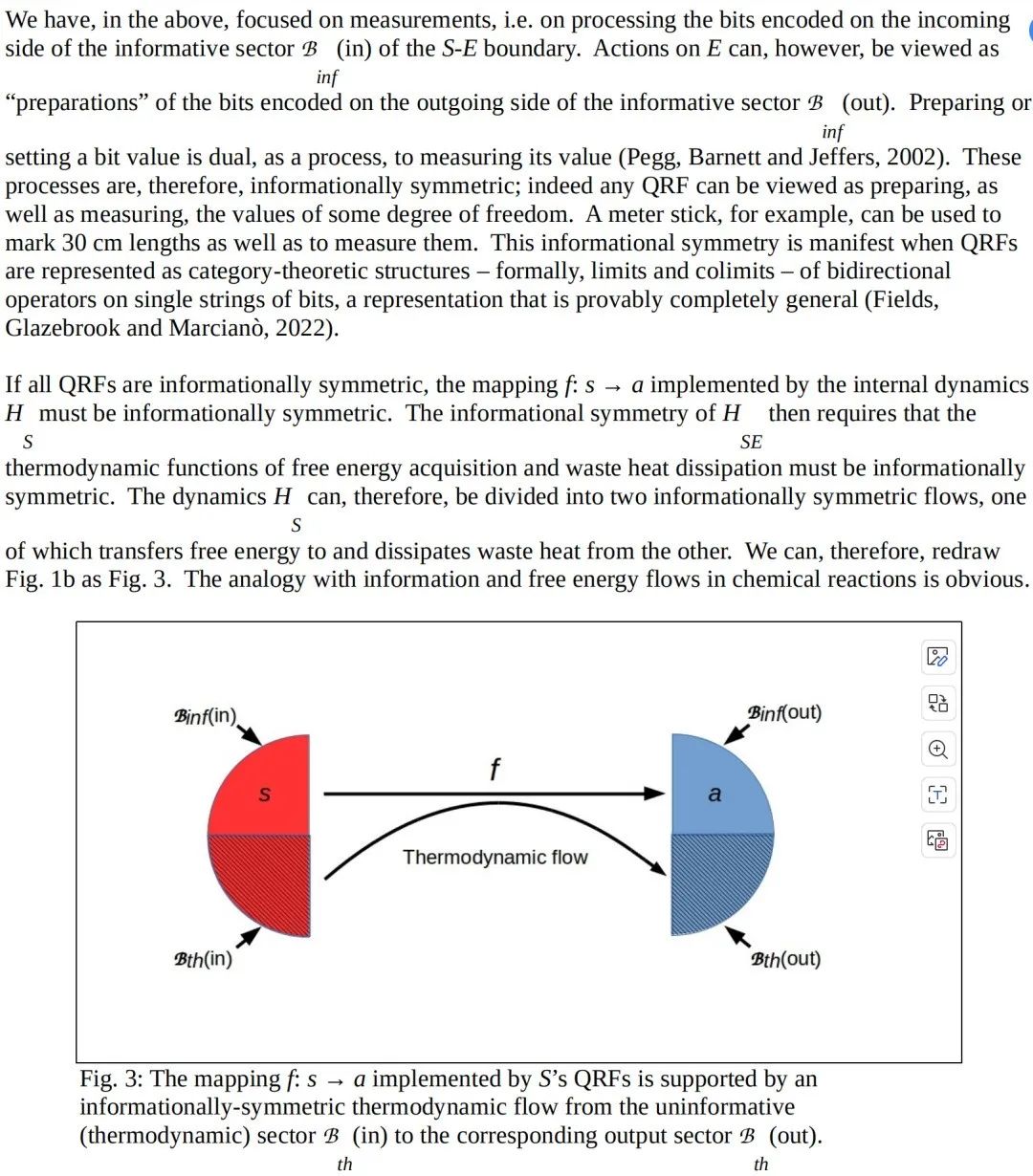
现在假设 S 具备非平凡的信息处理能力。在这种情况下，S 实现了某个非平凡函数 f:s→a，其中 s 是其信息性（在图 1 中未阴影部分）输入部分的瞬时状态，而 a 是其信息性输出部分的瞬时状态。自由能原理（FEP）要求这个函数平均而言要么是对 S 测量的 VFE（作为 E 状态的函数）的统计流形上的梯度下降，要么是无源流（Friston, 2019; Ramstead 等, 2022）。换句话说，函数 f 必须平均而言对 S 是 VFE 非增加的。

函数 f 由 S 的内部动态实现，我们可以将其表示为 S 的状态空间上的哈密顿算符 HS。因此，S 的内部动态 HS必须尊重 S 在信息性（s,a）部分 B 和非信息性、热力学部分之间的热力学不对称性。然而，E 的内部动态 HE按照构造是与 HS 条件独立的。因此，如果 E 也实现了非平凡的信息处理，那么没有要求，实际上也没有期望，E 的信息性和非信息性部分的边界与 HS 所分配的边界对齐。同样，也没有要求或期望 S 和 E 具有相同甚至类似的自由能使用效率或废热排放效率。一个相互作用伙伴视为信息性信号（无论是传入还是传出）的东西，可以被另一个视为非信息性的“噪声”，即废热输出或自由能输入。跨越 B 的有意义的通信，首先需要克服这种热力学不对称性。正如我们将看到的，形态——有效地，B 的几何化——提供了一种实现这一点的方法。

2.3 状态测量是参考系依赖的

为了理解 S 能够测量什么，以及 S 能够“知道”关于 E 的什么，回顾一下我们在实验室中作为科学家是如何进行测量的，这会很有帮助。考虑用一把具有 1 毫米精度的米尺来测量长度。这把米尺物理地编码了一个长度标准——米——并且通过永久且不可移动的刻度标记，物理地编码了它可以测量的可能结果长度，每个刻度标记之间相隔测量精度的一半。米尺所编码的标准是任意的，但通过编码它，米尺使得在不同时间对不同物体的测量能够进行比较。比较过程依赖于两个假设：1）米尺的长度，以及“1 米”的含义，不会改变；2）刻度标记的数量和位置，传统上称为“指针位置”，也不会改变。物理地编码这两个假设使得米尺成为一个参考系（RF）；它作为一个参考，使得其他长度能够有意义地进行比较。参考系既是物理对象，也是语义对象：它不仅赋予测量一个结果值，还赋予其意义。

人类观察者广泛使用参考系，包括实验室设备，以及像昼夜周期和地球重力场这样的非人工制品。然而，使用外部参考系总是需要观察，而这些观察必须能够相互比较才有意义。因此，使用外部参考系需要编码一个内部参考系。人类和其他生物编码了内部的空间、时间、振动、化学和电磁参考系，细胞周期、膜电压和各种化学浓度的参考系是一些最古老的参考系（Fields 和 Levin，2020c；Fields, Glazebrook 和 Levin，2021）。内部参考系为生物解决了“意义问题”（Froese 和 Taguchi，2019）。

内部参考系显然嵌入在复杂的系统中，例如生物体。用上面的语言来说，系统的任何内部参考系 S 都是由 HS 实现的。这表明内部参考系可能无法通过外部观察完全描述。实际上，从原则上讲，所有参考系，无论是内部的还是外部的，都是由必须至少在微观尺度上被视为量子系统的系统物理实现的。因此，它们是量子参考系（QRFs；Aharonov 和 Kaufherr，1984；Bartlett, Rudolph 和 Spekkens，2007），并且编码了“不可替代”的信息，即无法通过任何有限的经典比特字符串完全指定的信息（Bartlett, Rudolph 和 Spekkens，2007）。这意味着量子参考系不能通过共享比特字符串，即通过经典通信来共享，而只能作为独特的物理系统进行转移（Fields 和 Marcianò，2019）。因此，内部量子参考系在原则上是不可共享的。事实上，当两个不同的系统接近共享一个内部量子参考系时，它们会变得纠缠，并失去作为不同系统的身份（Fields, Friston, Glazebrook 和 Levin，2022）。

2.4 分层测量在所有尺度上普遍存在

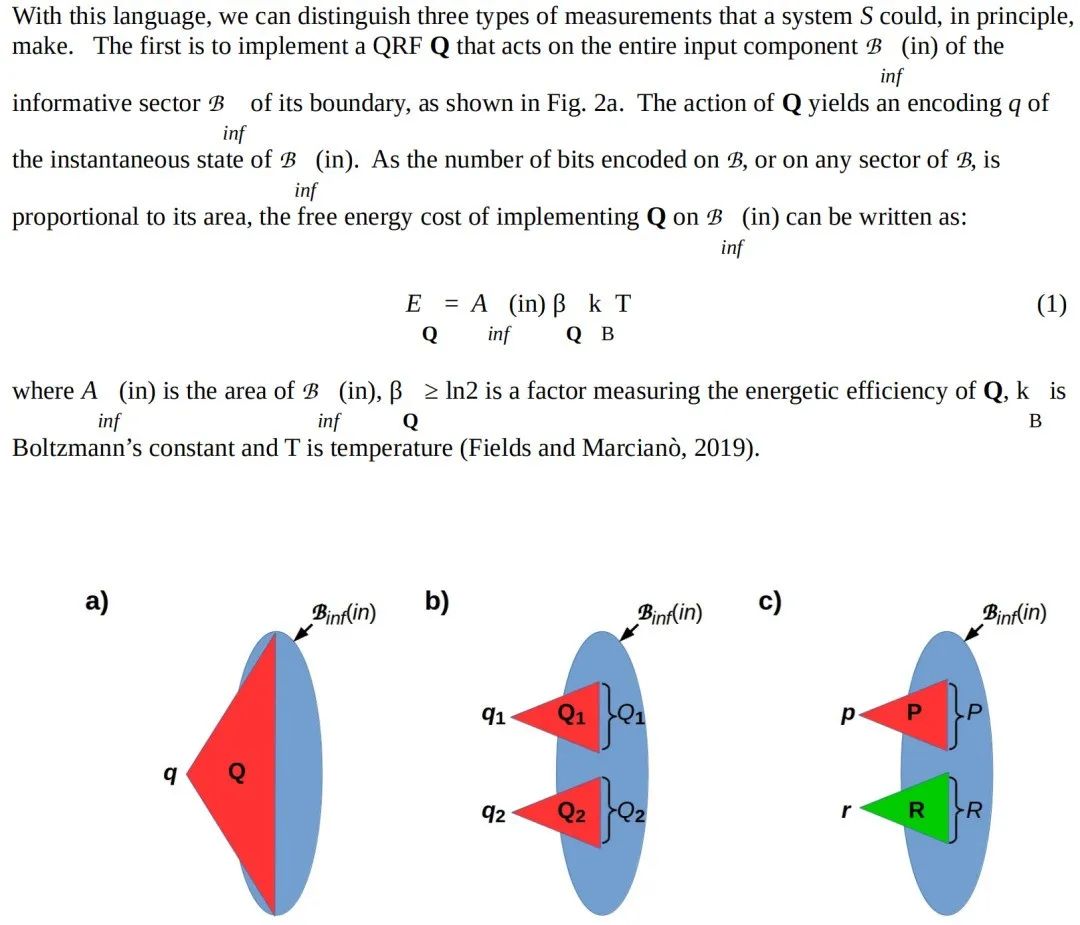
2.4.1 专门化的扇区测量

图 2c 展示了一种专门化的扇区测量形式。在这里，扇区 R 需要保持一个固定状态 r；因此，扇区 P 的测量状态具有形式 p=(p∣r)。在这种情况下，不相交的联合 PR 作为一个外部参考系（RF），具有固定的参考部分 R 和指针部分 P；PR 的“感兴趣状态”是其“指针”状态 p。所有可感知的对象，或者用 Friston（2019）的话来说，所有时间持久的事物，都具有这种复合形式：不变的参考扇区 R 允许将对象识别为“与之前测量的相同事物”，而可变的指针扇区 P 显示感兴趣的状态。再次以实验室设备为例，这些设备必须通过测量尺寸、形状、颜色和位置等可观测量来区分它们的周围环境，然后才能确定信息性的“指针”读数，提供了一个典型的例子。

2.4.2 分层测量在生物学中的普遍性

转向生物学，很明显，图 2b 和 2c 所示形式的测量是普遍存在的，而图 2a 所示形式的测量则很少见，甚至可能不存在。在每一个瞬间测量和处理整个可检测的环境状态在计算上具有挑战性，并且在能量上代价高昂；生物体反而将它们的资源集中在显著和重要的事物上，在不同的时间部署不同的特定扇区的量子参考系（QRF）。将资源分配给显著和重要的事物是注意力系统（Fields, Glazebrook 和 Levin, 2021）的功能。

尽管在大脑较大的动物中，物体感知和比较测量是熟悉的，但在大脑较小或无神经的动物、植物和单细胞生物中，这些能力的特征描述得较少。然而，所有能够以状态特定的方式识别和对配偶或同类做出行为反应的生物体，都具备一定程度的物体识别能力，因此也具备图 2c 所示的测量能力。因此，这种能力延伸到了微生物世界。所有能够根据两个变量的值同时调节其行为的生物体，例如根据糖和盐的浓度，或者根据环境光和水的可用性，都具备图 2b 所示的测量能力。因此，这种能力甚至延伸到了微生物世界，并且据我们所知，它描述了所有生命形式。

相同的考虑也适用于细胞内尺度。需要辅因子或磷酸化以及底物的酶在其环境中执行图 2b 所示的测量，膜结合的通道、泵和受体也是如此，它们对局部膜电压和 GTP 或其他调节分子的结合都很敏感。结合 DNA 并扫描特定转录起始位点的 RNA 聚合酶（Kuehner 和 Brow, 2006）在其环境中执行图 2c 所示的测量：首先将 DNA 分子识别为一个物体，然后检测该物体的特定状态——一个特定的碱基序列模式。空间组织的细胞内通路越来越被认为能够执行复杂的多输入计算，这不仅在神经元中（Gidon 等，2020），也在非神经细胞中（Kramer, del Castillo 和 Pelkmans, 2022）被认可，基础认知运动长期以来一直基于生化和行为数据提出这一观点（Maturana 和 Varela, 1980; Pattee, 1982; Stewart, 1996; di Primio, Müller 和 Lengeler, 2000; Lyon, 2015; Baluška 和 Levin, 2016; Baluška & Reber, 2019; Levin, 2019; Lyon, 2020）。

2.5 QRF的层次结构是MCA

在每个瞬间，映射 f:s→a 都是由输入和输出两侧的某种量子参考系（QRF）层次结构实现的；我们之前已经展示了皮层神经元如何实现 QRF 层次结构（Fields, Glazebrook, 和 Levin, 2022）。在任何瞬间部署哪些 QRF 决定了一个测量上下文（Fields 和 Glazebrook, 2022; Fields, Friston, Glazebrook, 和 Levin, 2022）；在上下文之间的切换是一种元处理功能，作为 f:s→a 的一个组成部分，它本身必须由一个（固定的）QRF 层次结构实现（Kuchling, Fields 和 Levin, 2022）。层次结构中的每个 QRF 都是一个具有自己输入、输出、电源和语义的独立计算系统。因此，QRF 层次结构是一个典型的多尺度能力架构（MCA）。

3. 自组织是由热力学驱动的

3.1 “环境”是一个活跃的主体

我们现在可以利用这些概念工具来理解自组织，不仅在同一尺度内，而且更有趣的是，作为一种在更大尺度上产生复杂性的热力学驱动过程。这将使我们能够在单一的形式框架内将生命起源模型与进化和发育模型联系起来，并理解从原细胞到细胞，再到多细胞系统的转变是如何由自由能原理（FEP）驱动的。

FEP 已经被证明为同一尺度内的自组织提供了一个通用模型（Kirchhoff 等，2018；Friston，2019）。简要总结，变分自由能（VFE）最小化对应于保持一个接近非平衡稳态（NESS）的状态。当内部过程——即内部动态 HS——足够准确地预测环境对马尔可夫毯（MB）的作用以维持 MB 的完整性，从而维持内部状态的条件独立性时，就实现了这一点。这被称为“自我证实”（Friston，2019），在生物系统中对应于维持稳态/适应性（Friston，2013）。在这种情况下，内部动态 HS，特别是它所实现的量子参考系（QRF）层次结构，可以被视为环境 E 行为的生成模型，特别是 E 对 MB 的作用。

我们之前也展示了如何通过在局部环境中产生并聚集“副本”来减少 VFE 是一个可行的策略（Fields 和 Levin，2019）。这些副本将系统与开放环境隔离，降低了其不可预测性。副本的行为类似于系统的行为，从而增加了可预测性。虽然这个模型是为生物细胞制定的，并展示了从 FEP 的角度来看多细胞性如何具有优势，但它也适用于更大的尺度，民族、语言或宗教群体以及社交媒体“回音室”是明显的例子。

在这里，我们采取了一个不同但互补的视角。开放系统的“环境”通常被视为被动的：作为一个热力学或物质交换资源、一个环境场，或者简单地说是一个热浴。在 FEP 文献中，环境通常只是一个不确定性的来源。对于生物系统来说，这显然是不现实的：一个生物体的环境主要由其他生物体组成，包括同类和其他物种。同样，生物分子的环境主要由其他生物分子组成，群体的环境主要由其他群体组成，等等。这些“其他”是追求自己议程的活跃主体，正如在博弈论模型中明确表达的那样。

自由能原理（FEP）不仅允许，而且在完全一般化的视角下，要求采用这种博弈论的视角。FEP 适用于所有具有马尔可夫毯（MB）的系统，并将所有这样的系统描述为变分自由能（VFE）最小化的主体。任何系统的环境都与该系统共享一个马尔可夫毯，正如图 1a 所明确显示的那样。因此，任何系统 S 的环境 E 也是一个 VFE 最小化的主体。对于 E 来说，其唯一的 VFE 来源是 S；因此，E 实现的任何生成模型都是 S 对其马尔可夫毯的行为的生成模型。假设 E 的生成模型是随机的——即 E 仅作为一个资源发挥作用——这是一种非常特殊的情况，对于生物学来说基本上是无关紧要的。现实中的环境是活跃的主体，正如我们通常更感兴趣的系统一样。

3.2 环境的作用是增加系统的可预测性

当我们把E视为一个主动的主体时，其行动的目标就变得清晰了：E的作用是减少其测量到的变分自由能（VFE）；因此，它通过其生成模型来增加S行为的可预测性。特别是，E的作用是增加S在其边界（MB）上的行为的可预测性。从E的角度来看，S的行为变得越来越可预测，对应于S“失去自由”，因此S的熵相对于E增加，正如在上文第2.2节中讨论的那样。前一节的考虑同样适用于S和E；为了理解E对S的作用，我们必须考虑E的信息处理能力，即其分层的QRF（质量反应场）。特别是，重要的是要理解E是否将S的行为视为信息输入，反之亦然（Fields, Friston, Glazebrook和Levin, 2022）。

一个S将自身的“副本”插入到E中的模型（Fields和Levin, 2019）实际上是一个E部署能够“理解”S行为的QRF的模型，如图4a至4c所示。从S的角度来看，副本是E的组成部分——或者更准确地说，副本的行为是E的行为的组成部分，这些行为由S在其MB处测量——至少是部分可预测的，因此对S“有意义”。随着副本的数量从零（图4a）增加到一个（图4b），再到多个（图4c），E的整体行为变得越来越可预测。因此，从自由能原理（FEP）的角度来看，S将自身的副本插入到E中是有利的（Fields和Levin, 2019）。然而，对E来说也是如此：随着E获得S的副本并整合它们的QRF，S的行为变得更加可预测。正如前面提到的，当考虑实现人类语言理解或其他社会文化实践的QRF时，这种对称动态变得显而易见。如果公司E拥有会说客户S语言的员工C，那么E可以更好地预测S的行为。

到目前为止，我们已经考虑了交互H<sub>SE</sub>和S与E之间的边界B。然而，我们可以在联合系统SE中选择任何边界，只要它作为MB，使得它所分隔的两个系统的状态在条件上相互独立。因此，假设图4d中所示的边界B'满足这个条件。划定这个边界定义了一个系统S'——它包括S——位于B'内部，以及一个环境E'B位于'外部。这两个系统通过在B'处的交互H<sub>S'E'</sub>相互作用。所有之前的考虑同样适用于这个新的交互。

现在我们可以考虑S将自身的副本插入到S'中（即插入由边界B'定义的内部），如图4e和4f所示。这样做对S的预测能力有上述讨论的后果。然而，这里我们将关注它对S'和E'的预测能力的后果。

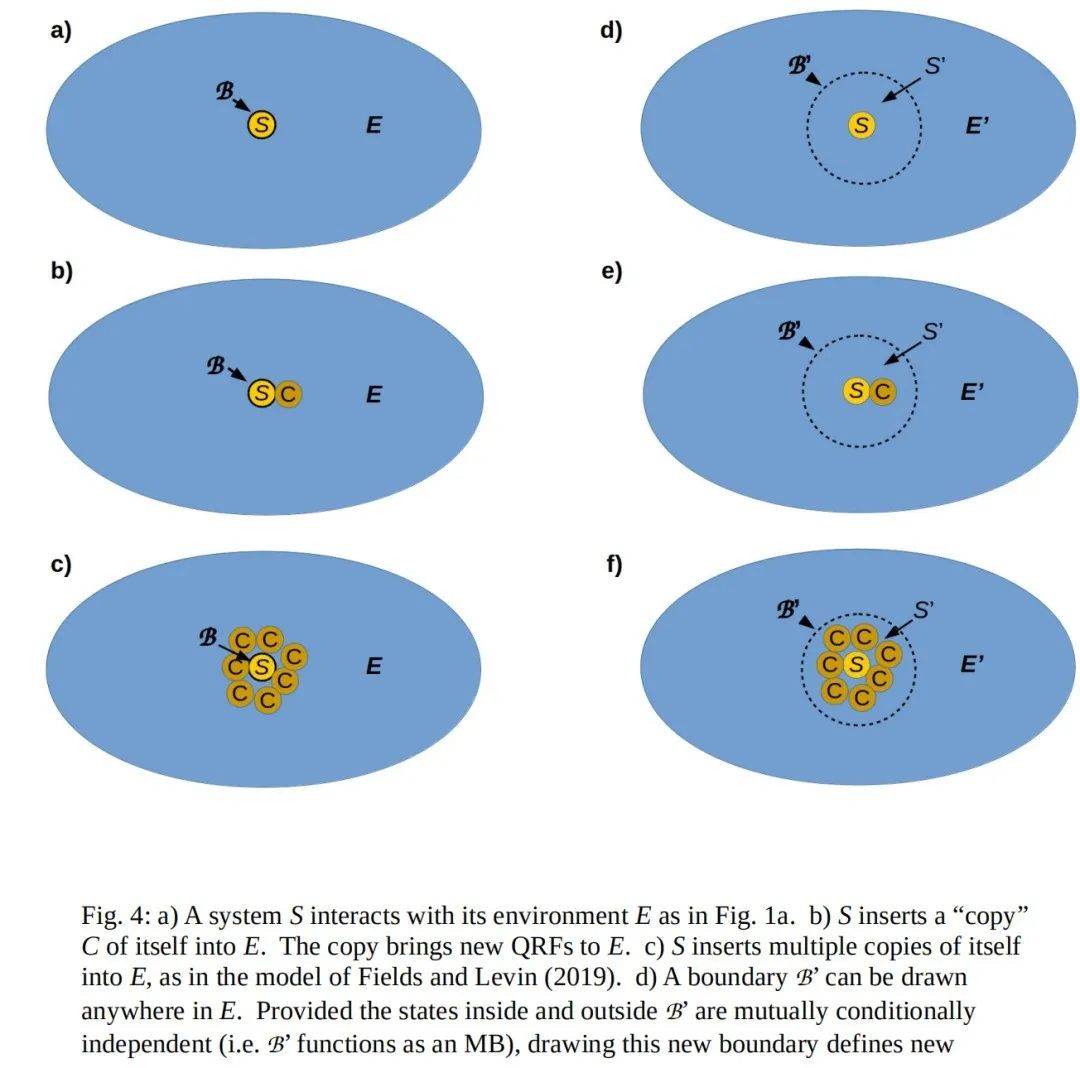
当边界从B移动到B'时，E的一些自由度变成了S'的自由度；因此，E'的自由度比E少，因此其计算能力也比E弱。特别是，E中直接测量B上编码的比特的任何QRF（质量反应场），在从E到E'的过渡中会丢失。然而，由于B'按构造起着MB（马尔可夫毯）的作用，S'的状态与E'的状态条件独立。在这种情况下，E可以分解为E = E'·(S'\S)，其中“\”表示集合，或者更准确地说是状态空间的减法。因此，由S'\S实现的任何测量B状态的QRF，都可以被视为将它们的结果值写在B'上。因此，我们可以将B'视为B的粗粒化。事实上，这种构造实现了“马尔可夫毯内的马尔可夫毯”（Kirchhoff等人，2018）的概念。

上述构造的一个特定例子是人们熟悉的，并且已经被详细研究过。假设S是一个感兴趣的系统，E'是一个观察者，例如一个人类观察者，而S'\S是一个环境场，例如可见光频率的光子场。在这种情况下，由S'\S实现的测量B的QRF（质量反应场）是散射光的相互作用，这些相互作用编码了S的属性，例如大小或形状。散射光在边界B'处影响E'，将关于S的编码信息传递给E'。编码的分辨率按B和B'面积比成比例的因子降低；因此，传递过程实现了粗粒化。显然，这种粗粒化信息传递过程仅仅是经典光学中视觉感知的标准机制。这种通过环境介导的测量已经在“量子达尔文主义”（Zurek, 2003; 2009）的名义下进行了广泛研究。它严重依赖于在B和B'处都施加条件独立性的边界。

对于E'来说，图4d和4f之间，或者图4a和4c之间有什么区别呢？副本C将它们自己的QRF（质量反应场）添加到S'\S中。这些QRF将关于S的信息传递给E'，同时也将关于E'的信息传递给S，正如Fields和Levin（2019）所讨论的那样。随着这些额外的QRF被插入到S'\S中，B'的面积以及其编码能力并没有发生变化。因此，边界B'必须对多个副本C贡献的QRF所写下的结果进行编码，为了简化，我们可以将其视为一个平均值的卷积。由于C都是S的副本，这些结果很可能是相似的，但通常不会完全相同。因此，一般来说，在图4f中，与图4d相比，或者在图4a和4c之间，B'对关于S的信息进行了进一步的粗粒化处理。

粗粒化减少了不确定性，因为它降低了测量的分辨率；它用相对低分辨率的“宏观态”来代替高分辨率的微观态（Hoel, Albantakis和Tononi, 2013; Hoel, 2017）。因此，从E'的角度来看，用S的副本C填充S'\S会减少VFE（变分自由能），从而增加预测能力。如果副本C是多样化的，预测能力会增加得更多，因为B'所施加的粗粒化会“抹去”C写下的细节，尤其是当它们写下不同的结果时。因此，我们得出了一个相当令人惊讶的结论：

自由能原理（FEP）将推动任何系统S周围的外围环境E'对S采取行动，以便能够或促进将多样化的S的“副本”插入到S的直接环境中。

换句话说，自由能原理推动任何“有趣”系统周围的环境，使该系统能够自我复制，并将这些复制品自我组织成围绕系统的“身体”。因此，自我组织是在自由能原理下由环境驱动的。

3.3 环境驱动促进了生命的起源及其多样化

当我们考虑到动物或植物的繁殖时，上述令人惊讶的结论就变得不足为奇了：生殖细胞被有意地包裹在微环境中——种子、卵、子宫——这些微环境有助于它们的复制以及胚胎的自我组织。通常，正确的微环境对于自我组织过程的成功至关重要。

在生物工程和人工生命的情境中，这一点显然也是成立的；在这里，“环境”以人类实验者的身份，提供了自我组织所需的材料和微环境。正如所有好奇心驱动的实验一样，实验者作为环境的目标是增加未来的预测能力，即减少未来的VFE（变分自由能）。

生物工程和人工生命的情境突出了环境“接管”复制任务的能力，提供所需的副本C，并且有时甚至将它们插入到系统的直接微环境中。例如，在异种机器人的运动复制中，环境提供了所需的解离的非洲爪蟾（X.laevis）皮肤细胞（Kriegman, Blackiston, Levin和Bongard, 2021）。在自然发生的亲和聚集的案例中，环境也提供了“部件”，从独脚虫（Dictyostelium）的孢子形成、多种微生物席的形成到共生系统的复制，包括所有全生物体（holobionts）（Guerrero, Margulis和Berlanga, 2013; Gilbert, 2014; Bordenstein和Theis, 2015）。

从更广泛的角度来看，在每一个生物或生化复制的案例中，环境都提供了部件，以分子亚单位的形式，通过本质上是运动学的过程进行组装。在以基因为中心的新达尔文主义进化和发育观点中，DNA复制——作为进化和发育的基本“复制器”（Dawkins, 1984）——是一个由环境驱动的过程：环境提供了核酸、酶、自由能以及运动学过程所需的生物化学和热力学稳定的隔室。为什么呢？从自由能原理（FEP）的角度来看，环境这样做是为了增加未来的可预测性。制造更多相同类型的分子比制造随机组合的分子能产生更可预测的未来状态。

在生命起源模型中，环境同样提供了部件和稳定的微环境（Cornish-Bowden和Cárdenas, 2017; Bartlett和Wong, 2020）。自由能原理表明，它这样做的原因与在DNA复制或生物体繁殖的情况下相同：为了增加其未来的预测能力。生命系统对信息进行定位、组织和粗粒化。从环境的角度来看，这种分室化减少了VFE。

主动推理和自我表征争夺能量和记忆资源

4.1 时延认知光锥需要记忆事件

我们到目前为止讨论了系统间的信息交换和系统内的信息处理，但没有明确考虑稳健的主体行为所需的记忆资源。我们可以特别区分处理当前观察或执行当前行动所需的记忆，以及记录先前观察所需的记忆。前者实际上是由部署的质量反应场（QRFs）的结构编码的；在纯量子计算的极限情况下，它没有自由能成本。因此，它可以被视为隐性、程序性或语义记忆。后者可以实现为显式、声明性记录：先前获得的结果值的直接副本。它也可以通过程序化的方式实现，正如人类情景记忆似乎所做的那样，但执行这一程序的结果是对重建的结果值的编码。无论哪种方式，每个记忆事件都有自由能成本。

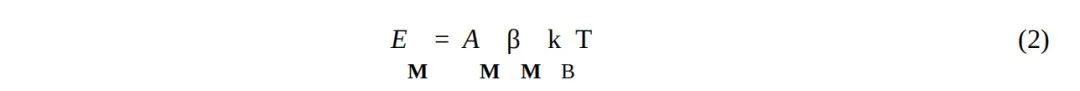
其中，AM 是编码的比特数，因此也是编码的有效面积，而 βM≥ln2 是记忆的效率。当S被视为一个量子系统时，经典信息能够编码的唯一位置是边界B（Fields, Glazebrook和Marcianò, 2021; Fields, Friston, Glazebrook和Levin, 2022）；因此，AM 是B上用于编码事件记忆的面积。需要注意的是，B上的编码使事件记忆暴露于环境E中；可能会额外消耗自由能（对应于更大的 βM 值）来保护记忆免受环境干扰，例如“遗忘”或修改。在人类情景记忆的情况下，这两种过程都是熟悉的。

规划未来行动需要事件表征，因此需要具有由方程2给出的成本的显式记忆资源（Boyer, 2008）。对遥远的、未被观察到的事件的表征也有类似的要求。因此，任何具有空间或时间上扩展的认知光锥的生物（Levin, 2021; 2022）都必须投入自由能资源来维持事件记忆。由于所有自由能都必须通过 Bth(in) 获得，这一要求在事件记忆与实时感知和行动处理（即主动推理）之间造成了权衡。对事件记忆进行粗粒化以降低其能量成本，为这种权衡提供了一种部分解决方案（Fields, Friston, Glazebrook和Levin, 2022），这种解决方案显然被人类情景记忆所采用。

4.2 明确的自我表征依赖于事件记忆

主体的概念隐含了自我表征这一观念。同样，我们可以区分一种纯粹隐性的、程序性的自我表征与一种明确的表征。细菌中的限制性酶或哺乳动物中的免疫系统是前者的例子，而心理学中常见的“自我”概念则是后者的例子。心理学中的自我被广泛视为一种构建（Blackmore, 2002; Metzinger, 2004; Graziano & Webb, 2014），这一观点现在已有相当多的神经功能学证据支持（Craig, 2002; 2010; Seth, 2013; Seth和Tsakiris, 2018）。正如在构建记忆的情况中一样，编码一个构建的自我表征需要自由能，正如方程2所规定的那样。

在人类中，自我被表征为既观察和执行记忆中和计划中的事件，也通过遥远的、未被观察到的事件受到其他事物的影响并影响其他事物。换句话说，认知光锥是被表征的自我的领域。认知光锥的体积限制了过去、现在和未来事件记忆的数量上限，而这些记忆的数量上限反过来又限制了自我可以被表征的不同情境的数量。因此，像人类一样的自我——我们对自我和主体性的人类直觉所基于的那种自我——严重依赖于事件记忆，尽管Strikwerda-Brown等人（2019）讨论了当前、过去和未来事件的不同表征之间的补偿机制。

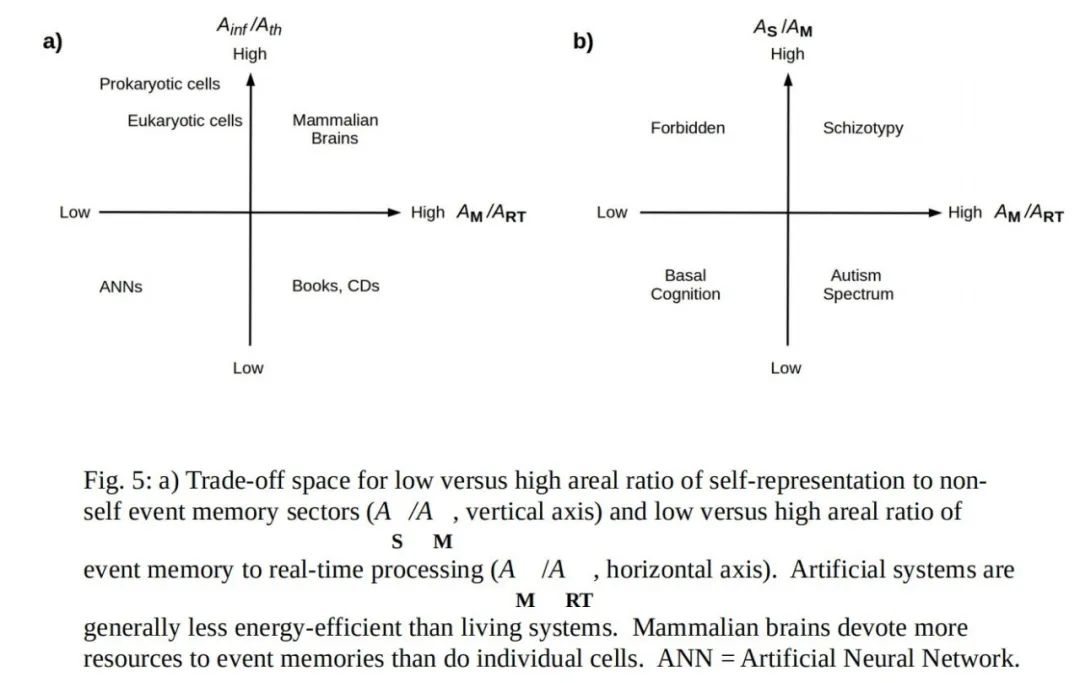
维持自我表征的自由能成本在将自我作为一个“角色”在多个记忆情境中维持与其他记忆用途之间造成了权衡，包括由生成模型支持实时主动推理的事件记忆访问。因此，高实时任务需求可以预期会“关闭”自我表征，这实际上在“心流”状态（Csikszentmihalyi, 2014）和其他自动化专家表现（Bargh和Ferguson, 2000）中被观察到，而在神经功能层面上，外部任务网络对默认模式网络的抑制（Chen等人, 2013），特别是在不需要自我相关处理的任务中（Andrews-Hanna, Smallwood和Spreng, 2014）。

这些与记忆相关的权衡在图5中以熟悉的系统为例进行了总结。然而，对我们目前目的来说，更有趣的问题是细胞、生物体或其他生物学感兴趣的系统的环境，甚至是它们的总近端环境，会落在这些权衡空间的何处。例如，一个典型人类的环境具有巨大的事件记忆容量，随着建筑环境，特别是建筑信息环境的持续扩展，这种容量稳步增加。这种记忆中有多少是明确地编码在一个典型人类与她的环境之间的边界上的？环境的记忆在多大程度上暴露于修改？这种容量中有多少是用于将环境自身表征为一个自我？虽然我们习惯于在涉及生物体时提出并回答这些问题，但当这些问题涉及环境时，它们听起来却很陌生甚至毫无意义。自由能原理的信息对称性要求我们严肃对待这些问题。

4.3 所有的心智都是“平的”

基于认知心理学和认知神经科学的数据，Chater（2018）得出结论，人类心智是“平的”——只有一种类型的感知、动机、计划或信念，即普通的、被体验到的那种。所有这些“心理状态”都包含解释性的语义内容。在Chater的模型中，心智是一个循环过程，从感知或记忆输入中生成语义解释。这些解释可以被意识所获取，而生成它们的过程则不能。

当前模型完全符合这种对心智的“平”观点，或者更广泛地说，对认知的“平”观点（Fields和Glazebrook, 2020）。事实上，它从第一性原理出发就要求如此。没有有限的系统，即只消耗有限能量的系统，能够分配足够的经典记忆来记录在某个时间间隔内其内部过程的完整执行轨迹。例如，数字计算机只记录其执行轨迹的抽象——因此是粗粒化。这种对自我表征的限制可以被视为哥德尔（1931）第一不完全性定理的后果，该定理排除了任何具有基本算术表达能力的形式系统的完整自我描述。对于量子系统来说，这种限制更为严格，因为每个状态转换，从原则上讲，都会转移不可替代的信息。因此，任何系统都在一个类似Chater的循环中运行，其中生成过程无法被完全记录，因此也无法作为经典信息被访问。我们可以将这一基本限制总结为：没有任何系统能够完全表征自己的QRFs（质量反应场）。

在自由能原理（FEP）的背景下，很自然地将系统所感知到的所有信息视为记录在其边界B上（Fields, Glazebrook和Levin, 2021; Fields, Friston, Glazebrook和Levin, 2022）。在这种情况下，Chater对认知的“平”概念立即就变得显而易见了。一个资源充足的系统可以记录并报告其内部过程的元认知抽象——根据定义这是一种粗粒化——但任何这样的报告都依赖于元处理器的能力（Kuchling, Fields和Levin, 2022）。这种抽象是即时自我表征的一部分。这些考虑同样适用于任何系统及其环境。

这种对心智的“平”概念，以及其对自我表征的原则性限制，有一个重要的后果：

没有任何系统能够完全预测自己的未来行为。

特别是，没有任何系统能够预测自己对新输入的反应，或者在新情境下对熟悉输入的反应。这一结果对实时认知有重大影响，更广泛地说，对学习、调节性发展和进化也有重要影响。

4.4 热力学产生了框架问题（Frame Problem）

马尔可夫毯（MB）的存在，即边界B将S与E分隔开来，根据定义，阻止了S直接测量E的内部动态。因此，S实现的任何生成模型G，原则上只是一个关于E在B上的行为的模型，而不是E内部动态的模型。通过使用G来预测E未来在B上的行为，S实际上是在使用G来预测E的内部动态。因此，对S来说，(B, G)这对构成了一个接口，正如Hoffman、Singh和Prakash（2015）所定义的那样；特别是模型G指定了在B所定义的“屏幕”上出现的“图标”。用不同的模型G'替换G，会在接口上放置不同的图标，这些图标可能具有更多或更少的操作能力，并赋予不同程度的预测能力。

感知界面理论（Interface Theory of Perception，Hoffman、Singh和Prakash，2015）的一个核心结果是，由自然选择过程产生的模型G通常无法完全再现环境的结构或动态——例如底层的对称性。尽管这一结果最初是在涉及资源竞争的博弈论背景下证明的（Prakash等人，2020；2021），但在这里我们可以从一个更深层次的视角来看待它。B的存在阻止了S测量E的动态，因此S实际上只能通过E的行为来学习这些动态。然而，正如我们之前所看到的，E无法编码自己的动态；因此，它更无法在B上编码这些动态。因此，S无法通过被告知或通过任何由B介导的学习过程来学习E的动态。

这一结果可以用框架问题（Frame Problem，FP，McCarthy和Hayes，1969）来重新表述，这是人工智能（AI）中的一个经典问题。FP通常被表述为这样一个问题：使用比穷尽的显式列表更紧凑的某种表示方式来指定环境的属性，这些属性不会因一个动作而改变。显然，这相当于通过生成模型G来预测什么不会改变的问题。然而，从上述内容中，我们不仅看到S无法实现这样的预测，而且E也无法实现这样的预测。FP已知是不可解的，即有限图灵机无法判定；FP的解决方案将意味着解决了不可解的停机问题（Dietrich和Fields，2020）。在这里，我们看到它是由将S与E分隔开的MB的存在所导致的。因此，这是一个本质上基于热力学的结果。

5. 学习既不是完全被动的，也不是完全自主的

通过误差反向传播等算法进行的监督学习（Rumelhart, Hinton和Williams, 1986）仍然是机器学习（ML）中的主导范式，尤其是在应用环境中的深度学习系统中。相比之下，野生生物通常被认为通过无监督的自主探索来学习。而家养环境中的社会学习和训练则被视为介于这两种极端之间。

自由能原理（FEP）的信息对称性表明，完全被动的训练和完全自主的探索都不太可能作为嵌入并物理地与真实环境（而不是仅仅形式化的环境）相互作用的系统的模型。训练的目标是使一个最初不可预测的系统产生可预测的行为。换句话说，训练是一种减少变分自由能（VFE）的方法。然而，在实践中，它从未完全成功。即使在像人工神经网络（ANNs）这样完全形式化的系统中，训练也会产生不可预测的生成模型；这种不可预测性是人工智能（AI）中解释问题（XAI，Samek等人, 2021; Taylor和Taylor, 2021）的根源。尽管这种失败通常被认为是一个技术问题，但从上述内容可以看出，它有一个深刻的热力学根源。通过监督学习训练ANN涉及将ANN对训练集中项目的响应评估为正确或错误，然后反向传播一个误差信号。这种评估使用了实验者/训练者的生成模型G，而实验者/训练者是正在被训练的ANN的有效环境。训练后的系统行为随后会与同一个G进行测试。因此，即使对训练后ANN实现的算法有完美的了解，其与G的相关性以及因此其测试行为仍将不可预测，因为G本身是不可预测的。XAI问题之所以困难，部分原因是预测我们自己未来行为的问题本身就很难。

我们提到这些AI问题，不仅是因为它们适用于一般的工程系统，还因为它们也描述了自然生物过程。环境可以被视为通过上述第3节中描述的选择过程“训练”正在发展或进化的系统。这个过程即使是环境本身也无法完全预测。所有系统，无论其内部结构或动态如何，无论它们嵌入的环境如何，都对它们的环境（包括我们这些环境嵌入的观察者）和它们自己保持不可预测性。因此，如果将自主性定义为缺乏可预测性，那么所有系统都具有一定程度的自主性。然而，没有任何系统具有完全的自主性，即从环境训练中独立或不受环境训练影响的意义上。这一结果让人想起物理学中的“自由意志定理”，该定理指出，在相当合理的假设下，如果任何系统在其过去的光锥（这里指物理光锥，而不是认知光锥）中所有信息都不可预测，那么所有系统都具有这种属性（Conway和Kochen, 2009）。归根结底，这是条件独立性的结果，即分离边界B存在的热力学后果。

6. 结论

我们在这里看到了自由能原理（FEP）如何为多细胞生物系统（MCAs）提供了一个通用模型，这个模型既适用于自然系统，也适用于工程系统，并且适用于短时间尺度和长时间尺度。事实上，自由能原理抹去了自然系统和工程系统之间的区别。因为自由能原理将任何感兴趣系统的环境描述为一个主体，所以环境总是可以被视为“训练”或“设计”该系统。环境在为复制提供所需部件方面的普遍作用，无论是DNA分子、细胞、进化或构建的生物体，还是完全人造的、非生物的系统，都展示了这种设计方面的特性。当环境被视为一个工程师时，就清楚地表明“自我组织”总是环境辅助的自我组织。自由能原理告诉我们，任何这样的过程的产物，都旨在减少环境所测量的变分自由能（VFE），因此在某种重要意义上，它服务于环境的目标。

这种对环境及其与生物系统的相互作用的看法，显著扩展了生物学中关于什么是“正常”或“典型”的通常概念。异种机器人（xenobots）和嵌合体（chimeras）变成了范例，而不是异常。同时，也清楚地表明，环境以VFE减少标准的形式，从上到下编码了“目标形态”。在进化和发育中，以及在生命起源的情境中，环境聚集了一堆可能的部件，看看会发生什么。生命是环境进行的实验的一个成功结果。

为什么环境会聚集部件来创造一个生物系统，然后协助其复制呢？自由能原理提出了一个简单的答案：环境是一个创造新奇事物的主体，以便看看它能获得什么样的信息回报。环境是一个典型的主动推理主体。它的行为就像任何这样的主体一样。

这种思维方式暗示了一种实验策略，这种策略已经被尝试过，但从未系统地进行过：它暗示将胚胎或各种不同类型的细胞集合分离出来，将它们混合在一起，形成多样化的、“多元文化”的群体，并观察它们在各种环境中的行为。例如，我们能否制造出类似异种机器人的多起源嵌合系统？我们能否制造出类似地衣的全新共生复合体，其部件来自非常不同的谱系？沿着这些方向的实验，实际上是一种类似于标准基因工程的“重组生物学”，但它是用细胞而不是基因来完成的。重组基因工程的成功表明，在某些“合适”的环境中，重组生物学可能对细胞有效。这类实验的结果可能会大大增加生命的多样性，超越迄今为止进化所提供的多样性。

原文链接：https://doi.org/10.1016/j.biosystems.2023.104927

阅读最新前沿科技趋势报告，请访问欧米伽研究所的“未来知识库”

https://wx.zsxq.com/group/454854145828

未来知识库是“欧米伽未来研究所”建立的在线知识库平台，收藏的资料范围包括人工智能、脑科学、互联网、超级智能，数智大脑、能源、军事、经济、人类风险等等领域的前沿进展与未来趋势。目前拥有超过8000篇重要资料。每周更新不少于100篇世界范围最新研究资料。欢迎扫描二维码或访问https://wx.zsxq.com/group/454854145828 进入。