Java算法：二分法算法实现

原创作品，允许转载，转载时请务必以超链接形式标明文章 原始出处 、作者信息和本人声明。否则将追究法律责任。
作者： 永恒の_☆ 地址： http://blog.csdn.net/chenghui0317/article/details/10474405

一、前言

       当数组或者集合中存放的元素非常大的时候，想要跟踪具体某个元素的位置或者是否存在，常规方式是循环每一个元素直到为止。这样的方式效率非常低下，这个时候需要使用二分法来实现。

       二分法的解释是： 在一个按照升序排列的数组或集合中，首先判断数组的最中间的元素大于还是小于要查找的值，如果中间的元素大于查找的值，说明想要查找的值在这个数组的前半部分， 反之想要查找的值在这个数组的后半部分， 然后继续取出这个前半部分数组的中间元素 与要查找的值作比较，如此反复下去，直到找到为止。

二、二分法算法的实现

1、二分法与普通算法的比较实现方式

    <1> 普通循环查询指定的元素需要循环数组的每一个元素直到找到为止，所以使用一个普通的for循环即可实现；

    <2> 二分法的实现需要 两个下标变量（start和end）来控制查询数组的范围，默认是从0到数组的最后一个元素，然后需要获取数组的中间元素（下标为(start+end)/2的元素）与要查找的值作比较，如果这个元素大于查找的值，说明 要查找的值在数组下标0到(start+end)/2 之间，否则在下标(start+end)/2到数组最后一个元素之间。     所以 每次比较之前都是将查询的范围缩短一半，然后控制这个查询的范围依据就是根据上一次数组中间的元素与查找的值比较之后 数组的元素的下标来重新分配的， 以便提高效率。

具体代码如下：

public class BinarySearchDemo {
	int[] array = null;
	int count = 0; // 比较的次数
	
	public void init(){
		array = new int[100];
		System.out.println("****************初始化数组****************");
		for (int i = 0; i < array.length; i++) {
			array[i] = i+1;
		}
	}
	
	/**
	 * 普通for循环查询指定的数字例子
	 * @param num
	 * @return
	 */
	public int forExample(int num){
		System.out.println("****************使用普通循环查找****************");
		for (int i = 0; i < array.length; i++){
			count++;
			if(array.length - 1 == i && num != array[i]){
				System.out.println("抱歉，没有找到");
			}else if (num == array[i]){
				System.out.println(array[i] + "找到了，在数组下标为" + i + "的地方，查找了" + count + "次。");
				break;
			}
		}
		return count;
	}

	/**
	 * 二分法查询指定数字 的例子
	 * @return
	 */
	public int binarySearch(int num){
		System.out.println("****************使用二分法查找****************");
		int index = 0; // 检索的时候
		int start = 0;  //用start和end两个索引控制它的查询范围
		int end = array.length - 1;
		count = 0;
		for (int i = 0; i < array.length; i++){ 
			count++;
			index = (start + end) / 2;
			if(array.length - 1 == i){
				System.out.println("抱歉，没有找到");
			}else if (array[index] < num){
				start = index;
			}else if (array[index] > num){
				end = index;
			}else{
				System.out.println(array[index] + "找到了，在数组下标为" + index + "的地方,查找了" + count + "次。");
				break;
			}
		}
		return count;
	}

	public static void main(String[] args){
		BinarySearchDemo demo = new BinarySearchDemo();
		demo.init();
		int num = demo.array[40];
		demo.forExample(num);
		demo.binarySearch(num);
	}
}

执行上面代码之后的效果如下图：

所以，普通循环查找查找了41次，然而使用二分法查找了6次，节省了近6倍的查询时间，所以如果数组中数组元素非常大的话将大大节省查询的时间。

特别的，使用二分法 需要注意的是查询的数组必须是升序排列的，否则会找不到的指定的元素，因为查找的原理是根据元素所在的范围来分区的，所以直接被过滤掉了。 另外如果数组使用的是降序排列的 那么在二分法实现的判断应该倒过来，即array[index] < num 和 array[index] < num 判断的操作互换。

    如果没有排序的话，可以直接使用Arrays的sort方法进行排序之后再使用二分法查找一样可以实现。

具体实现代码如下：

import java.util.Arrays;
import java.util.Random;

public class BinarySearchDemo {
	int[] array = null;
	int count = 0; // 比较的次数
	
	public void init(){
		array = new int[10000000];
		Random random = new Random();
		System.out.println("****************初始化数组****************");
		for (int i = 0; i < array.length; i++) {
			array[i] = random.nextInt(array.length);
		}
	}
	
	/**
	 * 普通for循环查询指定的数字例子
	 * @param num
	 * @return
	 */
	public int forExample(int num){
		System.out.println("****************使用普通循环查找****************");
		long startTime = System.currentTimeMillis();
		for (int i = 0; i < array.length; i++){
			count++;
			if(array.length - 1 == i && num != array[i]){
				System.out.println("抱歉，没有找到");
			}else if (num == array[i]){
				System.out.println(array[i] + "找到了，在数组下标为" + i + "的地方，查找了" + count + "次。");
				break;
			}
		}
		long endTime = System.currentTimeMillis();
		System.out.println("此次查询共花费" + (endTime - startTime) + "毫秒的时间。");
		return count;
	}

	/**
	 * 二分法查询指定数字 的例子
	 * @return
	 */
	public int binarySearch(int num){
		System.out.println("****************使用二分法查找****************");
		long startTime = System.currentTimeMillis();
		Arrays.sort(array);
		int index = 0; // 检索的时候
		int start = 0;  //用start和end两个索引控制它的查询范围
		int end = array.length - 1;
		count = 0;
		for (int i = 0; i < array.length; i++){ 
			count++;
			index = (start + end) / 2;
			if(array.length - 1 == i){
				System.out.println("抱歉，没有找到");
			}else if (array[index] < num){
				start = index;
			}else if (array[index] > num){
				end = index;
			}else{
				System.out.println(array[index] + "找到了，在数组下标为" + index + "的地方,查找了" + count + "次。");
				break;
			}
		}
		long endTime = System.currentTimeMillis();
		System.out.println("此次查询共花费" + (endTime - startTime) + "毫秒的时间。");
		return count;
	}

	public static void main(String[] args){
		BinarySearchDemo demo = new BinarySearchDemo();
		demo.init();
		int num = demo.array[40];
		demo.forExample(num);
		demo.binarySearch(num);
	}
}

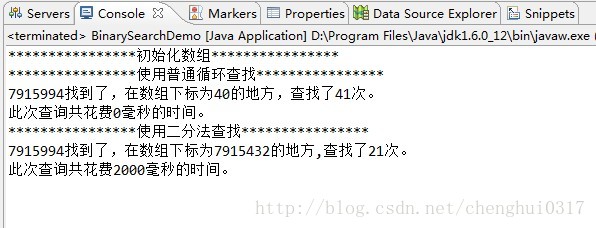
执行该代码的效果如下：

为什么普通查询使用了近0秒的时间，而使用二分法查找数量变少了但是查询的时间却增加到2秒了。 这是 因为使用Arrays.sort(array);这个方法，对于大数据的排序性能消耗是巨大的。

综上所述：使用二分法还是有局限性的，针对于升序排序的数组确实可以提高查找效率，但是如果是无序排列的话 这个时候要牺牲排序的性能来查找具体值，即使使用冒泡排序也得不偿失，所以最好不要这样使用。