算法导论13.3插入 练习总结

13.3-1 在 RB-INSERT 的第 16 行，将心插入的结点 z 着为红色。注意到，如果将 z 着为黑色，则红黑树的性质 4 就不会被破坏。那么为什么不选择将 z 着为黑色呢？

ANSWER：为了保持性质5，令红黑树的黑高不变。

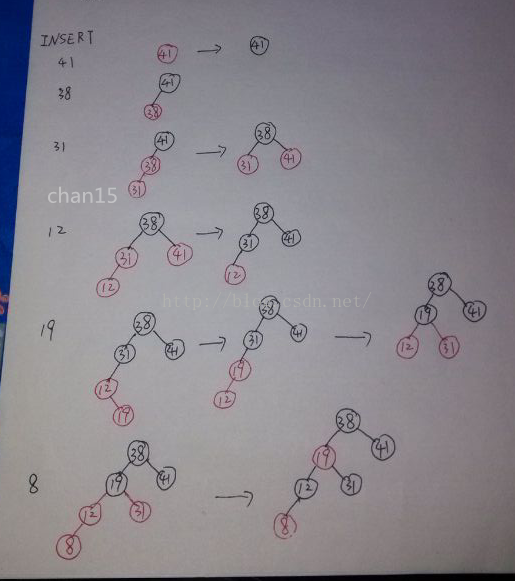
13.3-2 将关键字 41、38、31、12、19、8 连续地插入一棵初始化为空的红黑树之后，试画出该结果树。

ANSWER：

13.3-3 假设图 13-5 和图 13-6 中子树 α、β、γ、δ 和 ε 的黑高都是 k。给每张图中的每个结点标上黑高，以验证图中所示的转换能保持性质 5。

ANSWER：

13.3-4 Teach 教授担心 RB-INSERT-FIXUP 可能将 T.nil.color 设为 RED，这时，当 z 为根时，第 1 行的测试就不会让循环终止。通过讨论 RB-INSERT-FIXUP 永远不会将 T.nil.color 设置为 RED，来说明这位教授的担心是没有必要的。

ANSWER：在 RB-INSERT(T, z) 的伪代码中，只有 7、13 行会使祖先结点变成红色，而这两个都是 z.p.p.color = RED，且这个变色的前提是 z.p.color = RED，而 T.root.color = BLACK，所以不会使得 T.root.p(T.nil) 变为红色，所以教授的担心是没有必要的。

13.3-5 考虑一棵用 RB-INSERT 插入 n 个结点而成的红黑树。证明：如果 n ＞ 1，则该树至少有一个红结点。

ANSWER：对 RB-INSERT-FIXUP(T, z) 的伪代码中，①若出现 case 2 或 case 3，则第 16 行的 T.root.color = BLACK 并不会起作用；所以会运行第 13 行的 z.p.p.color = RED，即在循环不变式中会出现红结点，且退出循环后红结点颜色不会变更。②若循环中，只出现 case 1，则当 n ＞ 1 时，插入的结点必不为根结点，且插入的结点为红色，所以第 16 行不会改变插入的红结点的颜色。综上，至少存在一个红结点。

13.3-6 说明如果红黑树的表示中不提供父指针，应当如何有效地实现 RB-INSERT。

ANSWER：利用哈希表来保存父结点。