蜂窝小区最短距离实现 (数学归纳法+广度优先算法)

最新推荐文章于 2024-09-08 09:57:13 发布

快乐的霖霖

最新推荐文章于 2024-09-08 09:57:13 发布

阅读量8.5k

点赞数

分类专栏：基础算法

基础算法专栏收录该内容

161 篇文章

订阅专栏

蜂窝小区最短距离实现 (数学归纳法+广度优先算法)

题目描述：

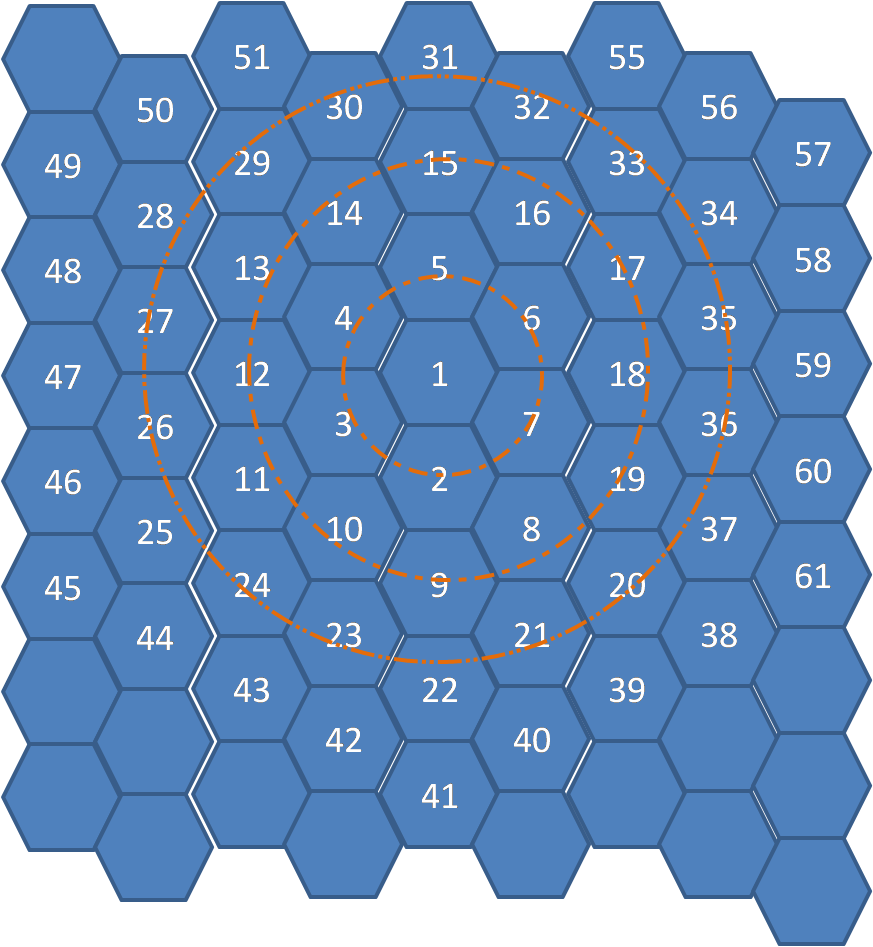
如图：由正六边形组成的蜂窝小区中，每个正六边形的编号也如图所示。求任意2点间的距离。(规定最大编号不超过100000)

分析：

1、求2点间的距离，第一印象就想到了广度优先算法（广度优先算法简单介绍：如图中的1点找编号为9的点时，可以第一次广度优先找到第二圈的所有元素，第二圈的元素再广度优先可以找到了9号点，所以必有一点可以从1点到9点，且距离为2）。但广度优先算法必须以知道任意点的相邻节点为前提。仔细观察又觉得点与点之间的关联又不是很有规律。

2、很容易看出6个点可以组成一个圆环，如：2,3,4,5,6,7 19,20,38,61,60,36等。为了找出规律，特按照编号顺序进行查找规律，那图看多了容易眼花，特意画了圆环虚线标识一个个圈，然后进行仔细分析；

3、得到所有点的相邻节点的前提是确定所有点的位置，然后再根据位置找规律得出其相邻的节点；

下面说下详细过程：

1、分析如何根据真实编号得到它所对应的圈号即圈内编号：

分析下每个圈的情况（以1号为1圈）：

圈号	容量	最小编号	最大编号
1	1	1	1
2	6	2	7
3	12	8	19
4	18	20	37

图示1

1)发现从第2圈开始，元素数量呈等差趋势，依次增加6，容量规律即有：size(n)=6*(n-1) ，同时n>=2;

2)继续观察发现每圈的最小编号减去相邻内圈的最小编号刚好等于内圈的容量即有cycle(n,1)-cycle(n-1,1) = 6*(n-2)，同时n>2(第2圈减第一圈规律不成立，n必须大于2)，其中cycle(n,1)表示第n圈的第1个元素；

3)根据数列求和可知：

cycle(n,1) -cycle(n-1,1) =6*(n - 2)

cycle(n-1,1)-cycle(n-2,1) =6*((n-1)- 2)

cycle(n-2,1)-cycle(n-3,1) =6*((n-2)- 2)

……

cycle(3,1) -cycle(2,1) =6*((3) - 2)

对以上等式分别左边与左边相加，右边与右边相加可知：cycle(n,1)-cycle(2,1)= 6*((3+4+…n)-(2*(n-2)))=6*((n-2)(n+3)/2-2*(n-2))= 6*(n-2)(n-1)/2=3(n-1)(n-2)

所以cycle(n,1)=cycle(2,1)+3(n-1)(n-2)，由图示1可知cycle(2,1)=2；所以cycle(n,1)=2+3(n-1)(n-2)，n>2；当n=2时，cycle(n,1)=2+3*(2-1)*(2-2)=2满足要求，所以cycle(n,1)=2+3(n-1)(n-2)的必需条件为n>=2；

3）由上可以推出：第n圈的m个元素可表示成：cycle(n,m)= 2+3(n-1)(n-2) -1+m，其中1<=m<6*(n-1)且n>=2，当n=1时，cycle(1,1)=1；

至此已经可以推出任意一个真实编号对应的圈号与圈内的编号了：

思路：对给定的任意真实编号与第n圈的极大值比较，若大于则取n+1圈继续比较，小于时停止比较，当前圈号为真实编号对应的圈号，根据cycle(n,m)公式可以计算出m值(圈内编号)；

2、分析一个点与所有相邻点之间的关系(直接考虑n>=2的情况，n=1时可做特殊处理)：

任意一个点在蜂窝小区中都有6个相邻节点，把它围在中间。

取第3圈的起始点8(第3圈的1号点)的相邻点进行分析，它有2个相邻点在其内圈上，2个点在当前圈，且在它左右；9号点（第3圈的第2点）则只有一个内圈节点，3个相邻外圈节点；

继续分析可知：第4圈的第1、2号点有2个内圈节点，第3号点只有一个内圈节点

……

继续拿第五圈的点进行分析……

可得出如下结论（以第n圈的圈内编号为m的点为例，n>2）：

1），当m<n-1时，它有2个内圈节点，圈内编号分别为m-1,m当m=1时，m-1取最大圈内编号，它有2个外圈节点，其圈内编号为m,m+1；

2）当m%n-1等于0时，它只有一个圈内节点，其圈内编号为：m*(n-2)/(n-1)，外圈编号为：n+m*n/(n-2),n+m*n/(n-2)+1,n+m*n/(n-2)+2；