找一棵树 (决策树 Decision Tree)

1. 一棵与众不同的树

决策树 (Decision Tree) 算法是机器学习的经典分类方法之一，它通过构造一棵具有决策能力的树来对样本进行分类。在这棵树当中，中间节点 (非叶子节点，No-leaf node) 代表一个个特征，分支 (Branch) 代表着按照对应节点划分样本的结果，终节点 (叶子结点，Leaf node) 代表样本最终的类别。

如下图 (a) 所示，我们收集了 Peter 同学每天打网球的历史记录，包括当天的天气 (Outlook)，温度 (Temp-erature)，湿度 (Humidity)，刮风 (Cloud) 等信息，以及 Peter 是否打球 (PlayTenis)。决策树算法尝试从这些数据中心构造出一颗决策树 (如 (b) 所示) 能预测未来某一天 Peter 是否出去打网球。

假设未来某天的天气情况是 (Overcast,Cool,High,Strong)，我们顺着这棵决策树从根节点 (Outlook) 按照天气情况访问到其叶子节点 (Outlook $\to$ Overcast $\to$ Yes)，于是就能预测这一天 Peter 会去打网球 (即 PlayTenis = Yes)。

决策树算法不一定会用到全部的特征，如上图 (b) 中的决策树就不包含 Temperature 特征。人们一般认为出现在决策树中的特征对于分类有影响，而没有出现在树中的特征则影响不大。

2. 对熵的宏观理解

熵 (Entropy) 的概念起源于物理学，在控制论、概率论、数论、天体物理、生命科学等方面也有应用，对人类甚至宇宙存在的意义、最终的结局方面也有推论¹。具体的来讲，熵表示这事物的无序程度²，换句话说，熵值越大，事物就越无序；熵值越小，事物就越有序。理解熵的含义对于决策树算法十分重要，这里我简单介绍一些物理学和信息论中的熵。

2.1 物理学中的熵

根据“热力学第一定律”，在封闭系统中，能量总量是不变的。即 能量不会凭空产生也不会凭空消失，它只会从一种形式转化为另一种形式。但是在现实生活中，我们发现能量的转化过程中，确实有一部分能量“消失”了，即能量并不能做到百分百的转换。举个栗子，在火力发电厂里，能量的转化形式是，

$$化学能(燃烧)\to 热能(蒸汽)\to 机械能\to 电能$$

但是上述转化效率只可能达到 30%，大部分的能量被转化成热能，辐射等耗散掉了 (我们无法使用)，这些无法使用的能量，我们定义为熵。随后，德国的理论家 克劳修斯 发现了 “熵增原理” (也称为“热力学第二定律”的克劳修斯描述)，即 孤立系统的熵值永远是永不减少 (只增不减)。

“熵增原理”揭露了自然世界中事物从有序到无序状态转变的规律。我们将其推广到现实生活中，如无人打扫的房间只会原来越乱，地球上的可供人利用资源会越来越少，宇宙最终走向消亡 (热寂说³) 等。从悲观的角度讲，任何事情的发展都摆脱不了热力学第二定律的束缚，我们的存在本身就是增加宇宙中的熵。而当宇宙中的熵达到最大值的时候，就是宇宙的毁灭之时。

2.2 信息论中的熵

在信息论中，熵 又称为 信息熵，信息熵表示信源的不确定性。对于随机变量 $X$ 而言，它的每个取值 $x_i$ 的取值概率是 $p_i$，那么其熵值 $H(X)$ 定义为，

$$H(X)=-\sum _{i=1}^k{p}_i\log (p_i)$$

我们可以理解为：熵越小，不确定性就越小，信息就越确定；熵越大表示不确定性就越大，信息就越不确定。如随机变量 $X$ 有 2 种结果，概率分布 $(x_1,x_2=0.1,0.9)$ 的确定性要强于 $(x_1,x_2=0.5,0.5)$。
我们分析了不同 $p_1,p_2$ 不同取值下的信息熵的值 $H(x)$。我们将其解释为：$p_1,p_2$ 越接近，不确定性就越大，我们就难以判断出 $X$ 到底取哪个值，于是熵就越大。

一些教程将熵写作期望的形式 $H(X)=E[I(X)]$，$I(X)$ 叫做 自信息量 ，记为 $I(X)=-\log (p_i)$。其实最终的结果都是一样的。另外，也有一些教程中将熵的值理解为分类的“不纯度”，即熵越小则纯度越大；熵越大则纯度越小。这个与“不确定性”的解释也是一样的。

3. 构造决策树的方法

一般来讲，构造决策树的过程是一个递归划分数据集的过程：针对数据集，选择一个特征，按照其值将样本划分为若干块子集，接着在每块子集中继续选择一个特征进行划分得到更多的子集，…，周而复始，直至子集中样本都属于同一类，或没有可划分的特征，或其他的停止条件达到为止。整个算法可以抽象为，

因此，算法的重点落在了 (1) 如何选取特征？ 和 (2) 如何设定停止准则？ 这两个问题上。

3.1 最优特征的选取

在每一步划分数据集之前，每一个特征都是备选的。我们要做的就是：从其中选出“最优”特征来对样本进行划分。那么如何选取这个“最优”特征呢？传统的决策树提供了 3 种决定方法，分别是 信息增益，信息增益率，和 基尼系数。这 3 种方法也对应着 3 种不同的决策树算法变体，即 ID3，C4.5，和 CART。

A. 信息增益 (Information Gain)，信息增益表述了划分样本之后熵的减少情况。令划分前样本集为 $D$，按特征 $f$ 的值划分的样本子集分别是 $D^1,D^2,...,D^v$。则此次划分造成的信息增益 $Gain(D,f)$ 定义为，

$$Gain(D,f)=H(D)-\sum _{i=1}^v\frac{|D^i|}{|D|}H(D^v)$$

其中 $|D|,|D^v|$ 分别表示集合 $D,D^v$ 包含的样本个数。为了更好的划分样本，我们每次选取信息增益最大的特征 $f^{\ast }$ 来对样本进行划分。

根据之前的信息熵 ($H$) 的定义，我们知道熵越大表示不确定性越大，即每个子集中正负类的比例比较接近，如 (0.5,0.5)，这样划分的效果不好，因为我们仍然无法确定样本的类别。相反，熵越小表示不确定性越小 (确定性越大)，即每个子集中正负类的比例相差悬殊，如 (0.1,0.9)，这才是我们期望的划分结果。于是这个可以看做是一个求解最优化的问题，即，

$$argma{x}_{f}Gain(D,f)$$

不过幸运的是，我们不用求解，我们只需要将不同的 $f$ 带入式子中去尝试并找到最大值即可。使用信息增益的决策树算法称之为 ID3 算法。

B. 信息增益率 (Information Gain Ratio)，信息增益率的提出是为了解决使用信息增益作为划分标准所带来的缺陷问题。人们发现 ID3 算法 对多值特征有偏好。一个极端的例子是，在选取最优特征 $f^{\ast }$ 时，我们选取样本的 id 值当做特征来进行划分，由于特征 id 的每一个值对应着一个样本，此时样本的确定性当然是最大的 (H(X)=0)，但是这样划分是无意义的，因为特征 id 并没有实际含义。于是，人们定义新的划分标准，即信息增益率 $Gain\_ratio(D,f)$，定义如下，

$$Gain\_ratio(D,f)=\frac{Gain(D,f)}{IV(f)}$$

可以发现信息增益率的计算其实就将原先的信息增益 ($Gain(D,f)$) 除以一个数 ($IV(f)$) 而已。式子中的 $IV(f)$ 是关于特征 $f$ 的常量，其定义如下，

$$IV(f)=-\sum _{i=1}^v\frac{|D^v|}{|D|}\log (\frac{|D^v|}{|D|})$$

这个 $IV(f)$ 乍一看很像之前信息熵的定义，其实它想表达的含义也十分的类似。对于那些取值非常多的特征来讲，它们熵很大；对于那些取值非常少的特征来讲，他们的熵很小。这样一来，信息增益率就可以有效的缓解信息增益对多值特征的偏好问题。

C. 基尼系数 (Gini Index)，基尼系数也是一个用来判断信息不确定性的指标。简单的讲，基尼系数越小越确定 (或越“纯”)，基尼系数越大越不确定 (或越“不纯”)。基尼系数定义为，

$$Gini(X)=\sum _{i=1}^k{p}_i(1-p_i)=1-\sum _{i=1}^k{p}_i^2$$

可以看出，基尼系数的计算没有对数操作 ($\log (p_i)$)，因此计算量会比熵要小。另外，基尼系数与熵表达的含义和趋势基本一致，均是越小表示越确定 (即越 “纯”)。

从数学的角度看，基尼系数的值近似于熵的值⁴。我们将 $f(x)=-\log (x)$ 在 $x=1$ 进行一阶泰勒展开，$f(x)=f(1)+\frac{f^{\prime }(1)}{1!}(x-1{)}^1=(1-x)$。
因此我们得到：$H(X)=-{\sum }_{i=1}^k{p}_i\log (p_i)\approx -{\sum }_{i=1}^k{p}_i(1-p_i)=Gini(X)$。

在每次选择特征的过程中，我们选择基尼增量 ($Gini\_Gain(X,f)$) 最小的特征作为“最优”特征进行样本集合的划分，

$$Gini\_Gain(X,f)=\sum _{i=1}^v\frac{|D^v|}{|D|}Gini(D^v)$$

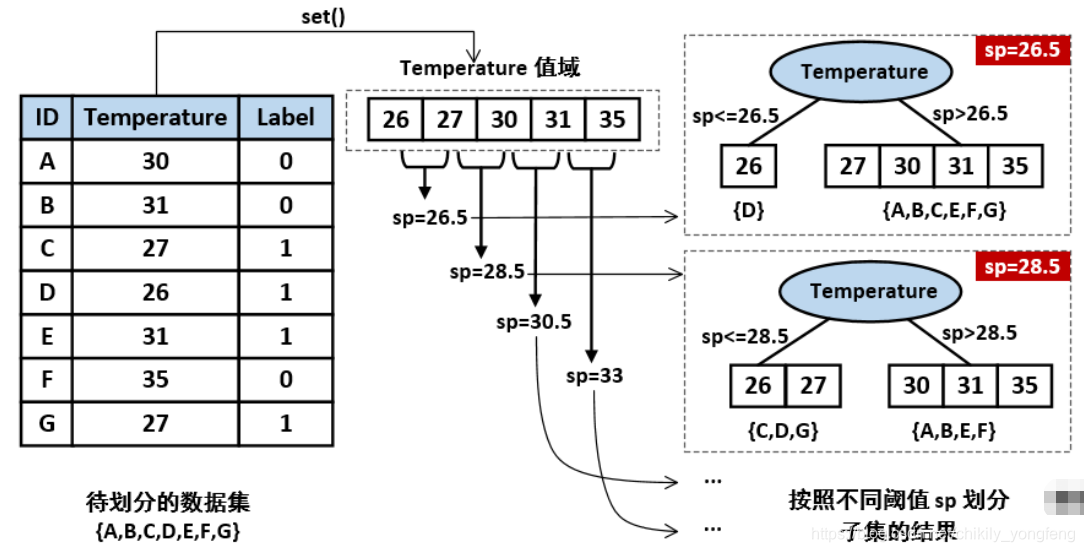
上述 3 个“最优”特征选择指标都是针对于离散型特征 ($f_d$)，如天气 (Outlook) 这个特征只能是 “Sunny, Overcast, Rain” 三者之中取值。因此我们按照 $f_d$=‘Sunny’，$f_d$=‘Overcast’ 和 $f_d$=‘Rain’ 划分成 3 个子集。对于那些连续型特征 ($f_c$)，它们可以取一系列实数值，此时我们设定一个阈值 ($sp$)，按照 $f_c\le sp$ 和 $f_c>sp$ 划分成 2 个子集。 找到最佳阈值 $sp$ 的方法如下如所示，

3.2 停止准则的设定

默认情况下，决策树的停止准则有 2 个：(1) 划分之前数据集只剩一类样本，(2) 划分之前已经用完了全部特征值。针对前种情况，我们将剩下的一类样本作为叶子结点；针对后种情况，我们将剩下多类样本作为叶子结点。除了上述的停止准则，在树的预剪枝操作中还包括很多的停止准则，如 (3) 树的最大高度，(4) 叶子结点包含的最小样本个数，(5) 最小划分子集的个数，(6) 最大信息增益小于某一阈值 等。

为了缓解决策树的过拟合的问题 (若分支太多，决策树相当于一个查找表)，人们往往会对生成的树进行剪枝操作 (Pruning)⁵。 剪枝操作可分为预剪枝 (Pre-pruning) 和后剪枝 (Post-pruning)。其中 预剪枝 操作就是在树的形成过程中判断递归过程是否该停止；后剪枝 操作指在树完成构建后判断哪些分支可以去除。

4. 用 Python 去构造这棵树

任务：以第 1 节中的 Peter 打网球的数据集 (图 (a) 所示) 为训练集构造一颗决策树 (ID3)，选取“最优”特征的标准为信息增益 (Information Gain)。

第一步：创建数据集。初始化特征集 X 和对应的标签集 y 组成训练集，训练集一共有 14 个样本，每个样本有 4 个特征 (Outlook, Temperature, Humidity, Cloud) 和 1 个标签 (PlayTenis)。在训练集中，所有的特征都是离散型特征，即存在有限个值。这里我们对集合 X 和 y 进行数组化 (np.array()) 操作是为了方便后续进行列的删除与查找操作。

import numpy as np
### input data X,y. X: feature space, y: class labels
X = [['Sunny','Hot','High','Weak'],
     ['Sunny','Hot','High','Strong'],
     ['Overcast','Hot','High','Weak'],
     ['Rain','Mild','High','Weak'],
     ['Rain','Cool','Normal','Weak'],
     ['Rain','Cool','Normal','Strong'],
     ['Overcast','Cool','Normal','Strong'],
     ['Sunny','Mild','High','Weak'],
     ['Sunny','Cool','Normal','Weak'],
     ['Rain','Mild','Normal','Weak'],
     ['Sunny','Mild','Normal','Strong'],
     ['Overcast','Mild','High','Strong'],
     ['Overcast','Hot','Normal','Weak'],
     ['Rain','Mild','High','Strong']]
y = ['No','No','Yes','Yes','Yes','No','Yes','No','Yes','Yes','Yes','Yes','Yes','No']

X = np.array(X)
y = np.array(y)

# feature names of X
feature_names = ['Outlook','Temperature','Humidity','Cloud'] 

第二步：构建决策树的递归框架 create_tree(X,y,features)。 该函数是构造树的递归函数，其输入是特征集 X，类标签集 y，和属性名称集 features。其输出是一个字典类型的树 my_tree。首先，判断两个终止条件是否满足，若满足则停止递归操作，若不满足则继续递归。其次，通过 select_best_feature() 函数来找到划分集合 X 的“最优”特征。最后，按“最优”特征的每个值对集合 X 进行划分 split_data()，得到划分后的集合 sub_X，和 sub_y。

def create_tree(X, y, features):
    # stop criterion 1: all samples belong to one class
    if len(np.unique(y)) == 1:
        return y[0]
    # stop criterion 2: no feature
    if X == []:
        return get_major_class(y)
    
    # select the best-fit feature to split the dataset X
    feature_id = select_best_feature(X,y)
    feature_name = features[feature_id]
    del features[feature_id]
    
    # define the subtree
    my_tree = {feature_name:{}}

    # obtain the values of best-fit feature
    feature_values = list(set(X[:,feature_id]))
    for val in feature_values:
        # split the X according to each feature value
        sub_X, sub_y = split_dataset(X, y, feature_id, val, True)
        sub_features = features[:]
        # create the tree iteratively
        my_tree[feature_name][val] = create_tree(sub_X, sub_y, sub_features)
        
    return my_tree

第三步：构造 get_major_class(y) 函数。该函数用来选取当前出现次数最多的类。这里，我使用一个字典来统计不同类出现的次数。当然，我们也可以借助 Collection 包来统计不同类出现的次数。

def get_major_class(y):
    # save <class, numbers> pair into a dictionary
    unique_class = dict()
    for i in y:
        if i not in unique_class.keys():
            unique_class[i] = 1
        else:
            unique_class[i] += 1
            
    # return the most frequency class
    max_key = None
    max_num = 0
    for i in unique_class.keys():
        if unique_class[i] > max_num:
            max_key = i
            max_num = unique_class[i]
    
    return max_key

第四步：构造 select_best_feature(X,y) 函数。该函数会选取划分数据集 X 的“最优”特征索引号。函数使用 infor_gain() 求出每个特征的信息增益，信息增益越大的特征即为最终的“最优”特征。若想要使用 C4.5 或 CART 算法，修改 infor_gain() 为求解信息增益率或基尼指数的函数即可。

def select_best_feature(X,y):
    num_features = len(X[0]) # number of remaining features
    results = []
    for i in range(num_features): # split X by each feature
        results.append(infor_gain(X,i,y)) # calculate their information gain

    max_id = 0
    max_res = results[0]
    for i in range(1, num_features): # select the feature that has the max information gain
        if results[i] > max_res:
            max_id = i
            max_res = results[i]

    return max_id

第五步：构造 infor_gain(X,i,y) 函数。该函数计算数据集 X 按照第 i 个特征划分时所产生的信息增益。

def infor_gain(X,i,y):
    unique_values = list(set(X[:,i]))
    origin_entropy = entropy(y) # entropy before split

    infor_gain = 0 # entropy after split
    for val in unique_values:
        sub_X, sub_y = split_dataset(X, y, i, val, False)
        infor_gain += len(sub_X)/len(X)*entropy(sub_y)
    
    return origin_entropy - infor_gain # return information gain

第六步：构造 entropy(y) 函数。该函数能根据类标签列表 y 来计算出 y 集合中的熵值。

def entropy(y):
    unique_class = dict() # each class y and its numbers
    for i in y:
        if i not in unique_class.keys():
            unique_class[i] = 1
        else:
            unique_class[i] += 1
    
    result = 0 # entropy result
    # H(X) = (-1) * sum [pi * log(pi)]
    for item in unique_class.keys():
        pi = unique_class[item]/len(y)
        if pi != 0 or pi != 1:
            result += (-1)*pi*np.log(pi)
    return result

第七步：构造 split_dataset(X, y, feature_id, val, flag) 函数。该函数将数据集 X 按照特征 feature_id 进行划分，若标志参数 flag==Ture，则在 X 中删除该列特征；否则 X 不删除该列特征。

def split_dataset(X, y, feature_id, val, flag):
    sub_idx = []
    sub_X = [] # index of X where the {feature_id}-th feature equals to val
    sub_y = [] # index of y where the {feature_id}-th feature equals to val
    for i in range(len(X)):
        if X[i][feature_id] == val:
            sub_idx.append(i)
    
    for j in sub_idx:
        sub_X.append(X[j])
        sub_y.append(y[j])
        
    if flag == True:
        # remove the feature column
        sub_X = np.delete(sub_X, feature_id, axis=1)
        
    return sub_X, sub_y

有了上述 7 步，我们就基本实现了一个最简单的决策树 (ID3)，现在我们在数据集 X，y 中检验一下它的性能。我们调用 creat_tree(X,y,feature_names)，就能得到如下结果。可以看到这个结果与我们在第一小节中的结果 (图 (b) 所示的决策树) 是一样的。

{'Outlook': {'Overcast': 'Yes',
             'Rain': {'Cloud': {'Strong': 'No', 'Weak': 'Yes'}},
             'Sunny': {'Humidity': {'High': 'No', 'Normal': 'Yes'}}}}

在书写每个函数时，为了节省博客空间，我去掉了函数的注释 (特别是对函数以及参数的定义)。另外，整个决策树也推荐写成面向对象的形式 (即构建一个决策树的类)，这样会更方便调用和维护。

5. 总结

简单总结一下，决策树算法是机器学习领域的经典分类算法，它的思想就是不断的寻找最优特征对数据集进行划分，最终生成一颗有决策能力的树。决策树的优点就是 (1) 模型的可视化非常好，即使非专家也能看懂并理解最终生成的树；(2) 数据集不需要归一化或缩放的预处理，这比逻辑回归等要方便。决策树的缺点也显而易见，那就是 (1) 容易过拟合，即使有那么多的剪枝操作也很难缓解这一问题，因此在实际应用中会使用随机森林或 Bagging 等方法来构造多棵树；(2) 处理大数据比较吃力，决策树的每次划分数据集都要对整体进行扫描，一种极端情况是内存放不下这么多的数据。

在使用决策树时，也应当注意这几个小技巧⁶：

• 数据集中特征个数大于样本个数，或特征个数较多时，容易产生过拟合。因此使用决策树之前可以考虑使用 PCA，ICA，或特征选择的方法对数据集进行降维，这可以很好的缓解决策树的过拟合问题。
• 另外一个缓解过拟合的方法就是设置 (i) 树的最大高度 和 (ii) 最小叶子结点的大小等，调整这些参数可以缓解过拟合问题。
• 类不平衡对决策树的影响也会比较大，为了防止大类造成的偏差，我们可以使用一些类不平衡的处理方法，如设置大小类的权值等。
• 可视化决策树对于数据分析很重要，通过可视化的结果，我们能显示地知道哪些特征比较重要，某个特征应该如何划分等信息。

---

1. 天人合一moonlight. 熵的理解 (博客). Link ↩︎

2. Wikipedia. 熵 Entropy (维基百科). Link ↩︎

3. 科学声音. 宇宙如何终结 (哔哩哔哩). Link ↩︎

4. Inside_Zhang. Gini 系数与熵的关系 (博客). Link ↩︎

5. 谢小娇. 包教包会决策树之决策树剪枝 (知乎). Link ↩︎

6. Sklean. Tips on practical use of desicion tree. Link ↩︎