Lintcode364 Trapping Rain Water II solution 题解

【题目描述】

Given n x m non-negative integers representing an elevation map 2d where the area of each cell is 1x1, compute how much water it is able to trap after raining.

 

给定n x m非负整数，表示二维的海拔地图，每个单元的面积是1 x 1，计算下雨后能捕到多少水。

 

【题目链接】

www.lintcode.com/en/problem/trapping-rain-water-ii/

【题目解析】

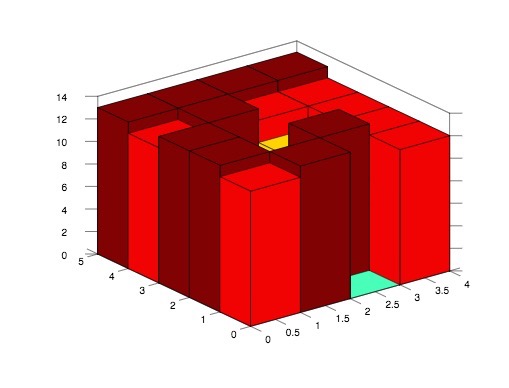
首先我们应该能分析出，能装水的底面肯定不能在边界上，因为边界上的点无法封闭，那么所有边界上的点都可以加入queue，当作BFS的启动点，同时我们需要一个二维数组来标记访问过的点，访问过的点我们用红色来表示，那么如下图所示：

我们再想想，怎么样可以成功的装进去水呢，是不是周围的高度都应该比当前的高度高，形成一个凹槽才能装水，而且装水量取决于周围最小的那个高度，有点像木桶原理的感觉，那么为了模拟这种方法，我们采用模拟海平面上升的方法来做，我们维护一个海平面高度mx，初始化为最小值，从1开始往上升，那么我们BFS遍历的时候就需要从高度最小的格子开始遍历，那么我们的queue就不能使用普通队列了，而是使用优先级队列，将高度小的放在队首，最先取出，这样我们就可以遍历高度为1的三个格子，用绿色标记出来了，如下图所示：

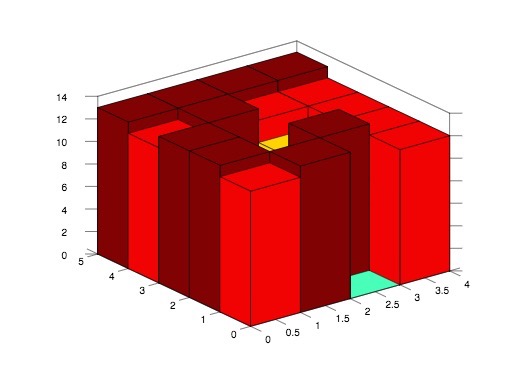
向周围BFS搜索的条件是不能越界，且周围格子未被访问，那么可以看出上面的第一个和最后一个绿格子无法进行进一步搜索，只有第一行中间那个绿格子可以搜索，其周围有一个灰格子未被访问过，将其加入优先队列queue中，然后标记为红色，如下图所示：

那么优先队列queue中高度为1的格子遍历完了，此时海平面上升1，变为2，此时我们遍历优先队列queue中高度为2的格子，有3个，如下图绿色标记所示：

我们发现这三个绿格子周围的格子均已被访问过了，所以不做任何操作，海平面继续上升，变为4，遍历所有高度为4的格子，如下图绿色标记所示：

由于我们没有特别声明高度相同的格子在优先队列queue中的顺序，所以应该是随机的，其实谁先遍历到都一样，对结果没啥影响，我们就假设第一行的两个绿格子先遍历到，那么那么周围各有一个灰格子可以遍历，这两个灰格子比海平面低了，可以存水了，把存水量算出来加入结果res中，如下图所示：

上图中这两个遍历到的蓝格子会被加入优先队列queue中，由于它们的高度小，所以下一次从优先队列queue中取格子时，它们会被优先遍历到，那么左边的那个蓝格子进行BFS搜索，就会遍历到其左边的那个灰格子，由于其高度小于海平面，也可以存水，将存水量算出来加入结果res中，如下图所示：

等两个绿格子遍历结束了，它们会被标记为红色，蓝格子遍历会先被标记红色，然后加入优先队列queue中，由于其周围格子全变成红色了，所有不会有任何操作，如下图所示：

此时所有的格子都标记为红色了，海平面继续上升，继续遍历完优先队列queue中的格子，不过已经不会对结果有任何影响了，因为所有的格子都已经访问过了，此时等循环结束后返回res即可。

【参考答案】

www.jiuzhang.com/solutions/trapping-rain-water-ii/

 

转载于:https://my.oschina.net/u/3782005/blog/1622061