使用随机梯度算法对高斯核模型进行最小二乘学习法

 

使用随机梯度算法对线性模型进行最小二乘学习法的算法流程：

1. 给θ以适当的初值。

2. 随机选择一个训练样本（例如，选择顺序为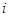的训练样本（，））。

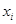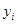3. 对于选定的训练样本，采用使其梯度下降的方式，对参数θ进行更新。

                                   

在这里，是名为学习系数的无穷小正标量，表示梯度下降的步幅。是顺序为的训练样本相对应的训练平方误差的梯度，表示梯度下降的方向。

                                     

  4．直接解达到收敛精度为止，重复上述②、③步的计算。

对于下式的高斯核函数模型：

                                           

                                      

下文显示了与其相对应的最小二乘学习法的随机梯度算法的运用实例。

将训练样本数n设定为50，高斯核带宽h 设定为0.3。在这个例子中，从随机、任意的初始值开始学习，经过1000次迭代计算，基本得到了近似的函数结果。

 

下面是这个例子的MATLAB程序源代码。

n=50;N=1000;
x=linspace(-3,3,n)';
X=linspace(-3,3,N)';
pix=pi*x;
y=sin(pix)./(pix)+0.1*x+0.05*randn(n,1);

hh=2*0.3^2;t0=randn(n,1);e=0.1;
for o=1:n*1000
    i=ceil(rand*n);
    ki=exp(-(x-x(i)).^2/hh);
    t=t0-e*ki*(ki'*t0-y(i));
    if norm(t-t0)<0.000001,break,end
    t0=t;
end
K=exp(-repmat(X.^2,1,n)+repmat(x.^2,1,N)'-2*X*x'/hh);
F=K*t;

figure(1);
clf;hold on;axis([-2.8 2.8 -0.5 1.2]);
plot(X,F,'g-');
plot(x,y,'bo');

程序运行的结果如下：

转载于:https://my.oschina.net/magicalee/blog/693951