机器学习理论三部曲

一、《机器学习理论三部曲》—— 引言 (Part I )

本文由北邮@爱可可-爱生活老师推荐，阿里云云栖社区组织翻译。

以下为译文

大多数人在小的时候被魔术师以及魔术技巧所迷住，并想弄明白其中的奥秘。有些人会带着这份迷恋研究到更深处并学习魔术技巧，有些人会接受专业的训练，而其他人会继续平庸下去。我在年幼时也尝试过魔术技巧并沉迷于其中，然而后来学习的是另外一种魔术，称作计算机编程。

编程确实酷似魔法， 和魔术一样，自学的现象在计算机编程世界占了上风。在过去的两年计算机开发者调查显示，超过一半的开发者是无师自通。我是在全职工作外学习这些计算机科学知识，当你已经工作后再尝试学习这些科目会是相当大的一个挑战。

如今我们可以找到很多关于计算机科学的视频、文章、博客以及自定进度点播MOOC课程，这几乎涉及每个方面。其中很多写的很详细并解释得很清楚，而且可以自由访问。这些资源的存在使得自我学习过程更加全面，使工作/生活/学习的平衡更易于管理，不幸的是，这并不是学习编程的完全正确趋势。

机器学习

虽然在大二就开始自学机器学习，但当毕业后才意识到自己错过了许多基础知识。所以在同样情形下，我很高兴发现自己避免了这种情况的发生，但机器学习理论不像计算机科学世界那么容易驯服。虽然互联网上充满了学习资源，但理论方面的内容是不一样的。即使你可以找到书籍、讲义、甚至是全部的讲座，但大多数不能像一系列博客、短视频或者MOOC提供的灵活性。

本文根据作者本身学习计算机科学的经验，给出了学习机器学习理论的这一系列文章，能够填补自主学习机器学习的理论与实践之间的差距，从而在征途上少一些艰辛。

这个系列是为了谁？

该系列意图是为了给机器学习理论方面提供简单的介绍，这将会对你是有利的，如果你是：

l  机器学习的从业者，并想深入了解详细过程；

l  机器学习的学生，尝试深入钻研机器学习理论并会喜欢一些宽松政策；

如果你是机器学习的初学者，这可能不是你的最佳起点。使用实际教程开始会更好。当你掌握了机器学习实践的窍门后，如果你觉得有必要，可以回到这里。

先决条件

理论需要数学知识，机器学习的理论也不例外。但是由于这仅仅是为了简单的介绍，不会钻研太深的数学分析，将更加注重理论的直觉与足够的数学知识以为了保持严谨。

大多数所需要的知识是：概率和随机变量，和微积分的基本知识。

注意事项

我仍然不是这个领域的专家，所以当你在这个系列中发现一些错误，请让我知道；

这仅仅是一个简单介绍，如果你想真正理解该领域，在阅读该系列的同时也要努力工作；

现在将机器学习问题快速公式化，以便建立起数学模型和框架

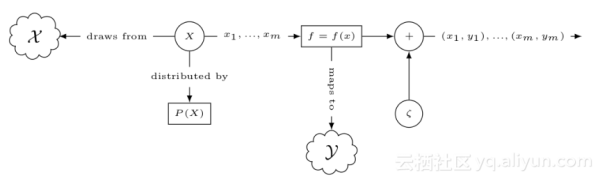
形式化学习问题

在这个系列中，将主要侧重有监督学习问题，数据集https://yqfile.alicdn.com/cfced9e187595ae164c5b0284f521f9b3fd4c4f4.png，其中xi是特征向量，yi是标签，问题是给定xi，怎么得到yi的值。比如说xi是具体医学测量结果的特征向量，yi是病人是否为糖尿病，我们希望从给定的医学测试结果中诊断是否患有糖尿病。

为了建立理论框架，重新梳理下已经知道的内容

1  知道从众多人口中随机采样的数据集中的值（xi,yi），具体的例子中的数据集是从众多可能患者中随机采样得到

将该例子公式化，两个随机变量X和Y表示xi与yi，且概率分布分别为P(X)和P(Y)；

2  我们知道X与Y之间有一些规则，并希望任意的XY对都能符合该规则，定义该规则，正式将其称为空间，X是从输入空间X中取值得到，Y是从输出空间Y取值得到；

3  特征值与标签之间有一定的联系，在某种程度上，特征值决定标签值，或者说Y的值是以X值为条件；

正式地，将其称作条件概率P（Y|X），利用该概率可以得到其联合概率密度P(X|Y)；

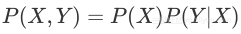
根据这三点，可以定义统计模型，下图形式化的描述了模型的处理过程

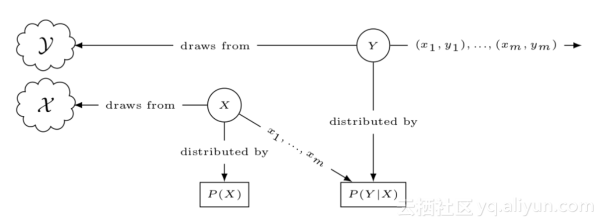
目标函数

机器学习过程的根本任务是理解条件概率分布P（Y|X）的性质，为了避免麻烦，下面介绍一些简单的工作。

可以使用均值和方差分解一个随机变量，均值是随机变量的中心，方差是测量随机变量在均值周围是如何分布。假设给定随机变量V和W，则

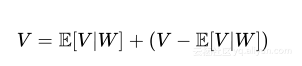
其中E[V|W]是随机变量V给W的条件均值，该均值可以将V的值分解为两部分。任意W与V的相关联值（wi,vi）的关系可以定义如下

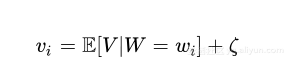
ζ表示噪声变量ζ的值，称为噪声分量，同样地定义统计模型（xi，yi）

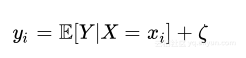
其f : X → Y的函数定义如下

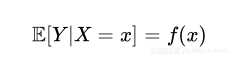
即条件概率是输入空间X映射到输出空间Y的函数，使用下列公式表示特征与标签的联系

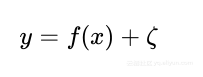
目标函数为f=f(x)，统计模型简化为

机器学习的任务简化为估计函数f。

假设

由于要对现存的每个函数进行评估，因此尝试对函数f进行假设，定义函数可能的空间为假设空间H。

如果假设函数f是来自ax+b，可以定义假设空间H为

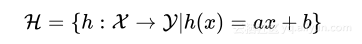
这是所有函数h映射输入空间到输出空间的集合，机器学习的任务现在是从H中挑选出一个具体的函数h，该函数能够最好的估计目标函数f。

损失函数

损失函数是用来评估假设函数估计目标函数的效果如何，定义损失函数（代价函数）

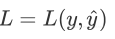
该函数是将从特征向量x中得到的估计标签y与真实标签y的差距

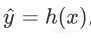
使用损失函数可以计算假设函数h对整个数据集的性能，分类错误或者经验风险定义为

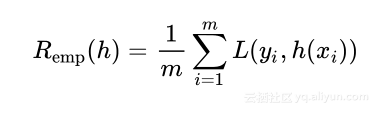
在这里不称作经验误差的原因是如果使用E表示误差，这会导致与期望值E标记的混乱，因此使用风险和R代替。通过定义的经验误差，机器学习过程需要选择最小的Remh(h)作为目标函数f的最优估计。

泛化误差

我们的目标是学习总体数据集的概率分布，这意味着假设应该对采样出的新数据也会有低的错误。这也说明这些表现好的假设在总体概率分布上有好的泛化，定义泛化误差：

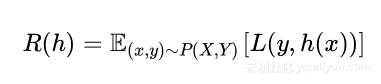
学习问题是否可解？

如果Remp(h)和R(h)非常接近，那么学习问题可解。问题转化为计算下述概率：

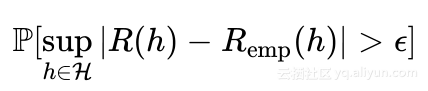
公式表示R与Remp之间的绝对差的最小上界大于https://yqfile.alicdn.com/c46fe657687292c24ec56787bfee66d8f95aec0a.png的概率，若该概率足够小，则学习问题可解。

参考文献：

l James, Gareth, et al. An introduction to statistical learning. Vol. 6. New York:springer, 2013.

l Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. The elements of statistical learning. Vol. 1. Springer, Berlin: Springer series in statistics, 2001.

l Mohri, Mehryar, Afshin Rostamizadeh, and Ameet Talwalkar. Foundations of machine learning. MIT press, 2012.

l Abu-Mostafa, Y. S., Magdon-Ismail, M., & Lin, H. (2012). Learning from data: ashort course

文章原标题《Machine Learning Theory - Part I》，作者：Mostafa Samir，译者：海棠

文章为简译，更为详细的内容，请查看原文

————————————————————————————————

二、《机器学习理论三部曲》—— 泛化界限 (Part II )

本文由北邮@爱可可-爱生活老师推荐，阿里云云栖社区组织翻译。

以下为译文：

上节总结到最小化经验风险不是学习问题的解决方案，并且判断学习问题可解的条件是求：

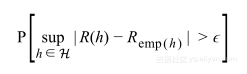
在本节中将深度调查研究该概率，看其是否可以真的很小。

独立同分布

为了使理论分析向前发展，作出一些假设以简化遇到的情况，并能使用从假设得到的理论推理出实际情况。

我们对学习问题作出的合理假设是训练样本的采样是独立同分布的，这意味着所有的样本是相同的分布，并且每个样本之间相互独立。

大数法则

如果重复一个实验很多次，这些实验的平均值将会非常接近总体分布的真实均值，这被称作大数规则，若重复次数是有限次m，则被称作弱大数法则，形式如下：

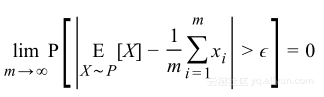
将其用在泛化概率上，对于单假设h有

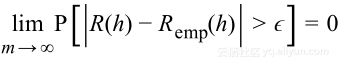
hoeffding不等式

集中不等式提供了关于大数法则是如何变化的更多信息，其中一个不等式是Heoffding不等式：

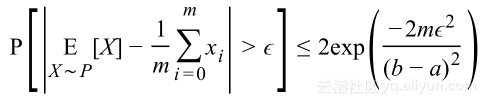
将其应用到泛化概率上，假设错误限定在0和1之间，则对于假设h有

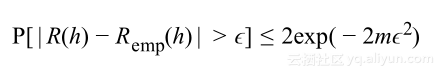
这意味着训练与泛化误差之间的差大于

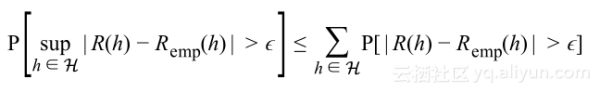
的概率是随着数据集的大小成指数衰减。

泛化界限：第一次尝试

为了针对整个假设空间都有泛化差距大于

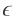
，表示如下：

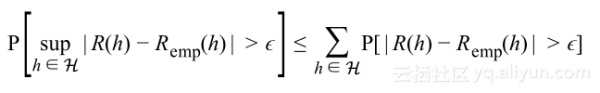
使用布尔不等式，可以得到

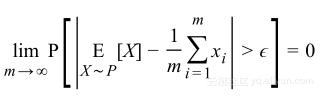
使用Heoffding不等式分析，能够准确知道概率界限，以下式结束：

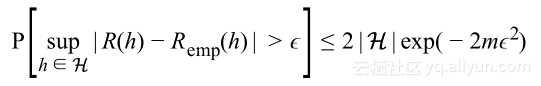
置信度1-δ有

使用基本代数知识，用δ表示

得到：

上式就是第一次泛化界限，该式表明泛化错误是受到训练误差加上以假设空间大小和数据集大小的函数的限定。

检验独立性假设

首先需要问自己是否每一个可能的假设都需要考虑？答案是简单的，由于学习算法需要搜索整个假设空间以得到最优的解决方案，尽管这个答案是正确的，我们需要更正式化的答案：

泛化不等式的公式化揭示了主要的原因，需要处理现存的上确界，上确界保证了存在最大泛化差距大于

的可能性。如果忽略某个单假设，则可能会错过“最大泛化差距”并失去这一优势，这不是我们能够承担的，因此需要确保学习算法永远不会落在一个有最大泛化差距大于

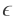
的假设上。

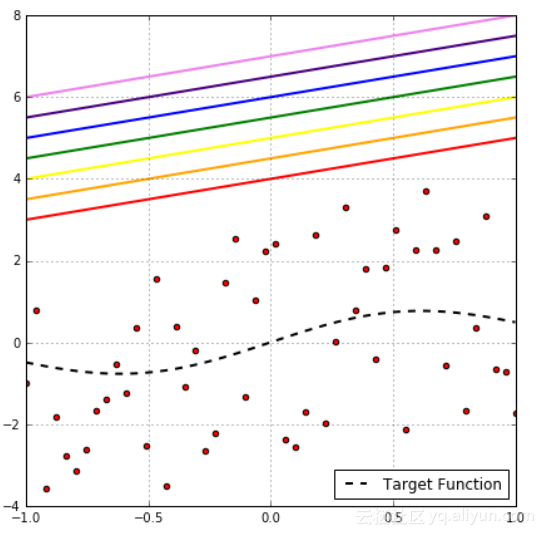
从上图可以看出是二分类问题，很明显彩色线产生的是相同的分类，它们有着相同的经验风险。如果只对经验风险感兴趣，但是需要考虑样本外的风险，表示如下：

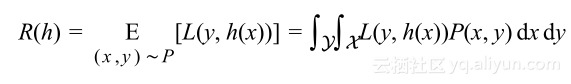
为了确保上确界要求，需要考虑所有可能的假设。现在可以问自己，每一个有大泛化差距的假设事件可能是互相独立的吗？如果上图红线假设有大的泛化差距大于

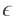
，那么可以肯定的是在该区域的每个假设也都会有。

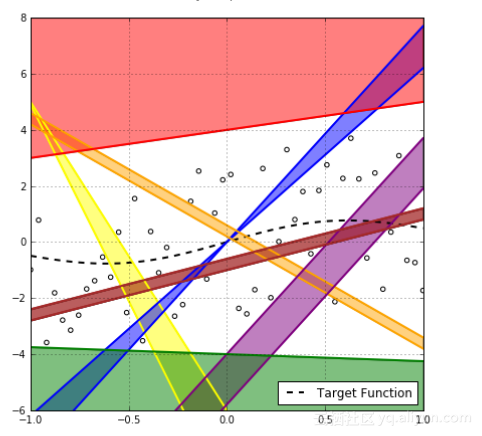
这对我们的数学分析是没有帮助的，由于区域之间看起来取决于样本点的分布，因此没有方法在数学上精确获取这些依赖性，于是这些统一的界限和独立假设看起来像是我们能够做的最佳近似，但它高估了概率并使得这些界限非常接近，性能不好。

对称引理

假设训练集是独立同分布，但不是只考虑数据集S的部分，假设有另外的数据集S’，大小为m，将其称作ghost数据集。使用ghost数据集可以证明：

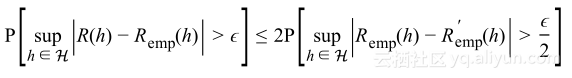
该式意味着最大泛化差距大于

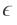
的概率几乎是S与S’之间的经验风险差概率大于

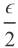
的两倍，这被称作对称引理。

生长函数

如果我们有许多假设有着相同的经验风险，可以放心地选择其中一个作为整个群的代表，将其称作有效假设并抛弃其它的假设。

假设在

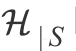
中的假设的独立性与之前在H的假设一样，使用一致限可以得到：

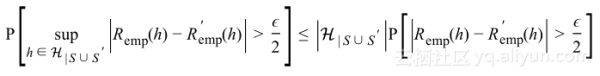
定义不同S数据集的标签值的最大数作为生长函数，对于二元分类情况，可以看到：

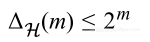
但由于是指数形式，随着m的增大而快速增长，这会导致不等式变坏的几率变得更快。

VC维

如果一个假设空间确实能够在数据点集上产生概率标签，我们可以说该假设空间打碎了该数据点集。但任何假设空间能打碎任何尺寸的数据集吗？下图展示的是2D的线性分类器有多少种方法标记3点（左边）和4点（右边）。

事实上，没有2D线性分类分类器可以打散任何4点的数据集，因为总是会有两个标签不能被线性分类器生成，如下图所示：

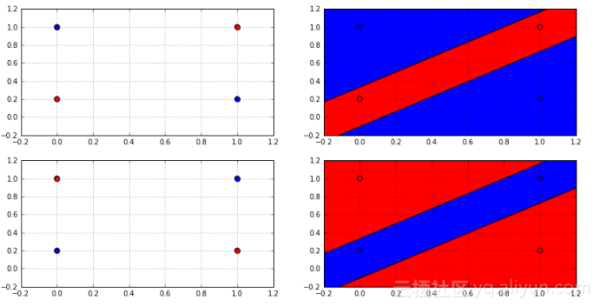
从图中的判定边界，可清晰知道没有线性分类器能产生这样的标签，因为没有线性分类器能够以这样的方式划分空间，这一事实能够用来获得更好的限定，这使用Sauer引理：

如果假设空间H不能打算任何大小超过k的数据集，那么有

K是空间H能够打碎的最大数量点，也被称作Vapnik-Chervonenkis-dimension或者VC维数。

生长函数的界限是通过sauer引理提供的，确实是比之前的指数形式好很多，运用代数运算，能够证明：

这样我们能够针对生长函数使用VC维数作为其替身，

将会是复杂度或者假设空间丰富度的测量。

VC泛化界限

通过结合公式1与公式2可以得到Vapnik-Chervonenkis理论，形式如下：

重新将其表述作为泛化误差上的界限，得到VC泛化界限：

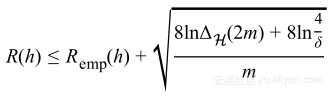
或者使用

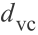
表示生长函数上的界限得到：

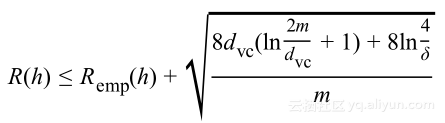
该式清晰并间接表示了学习问题是否可解，并针对无限假设空间，对其泛化误差有着有限的界限。

基于分布的界限

事实上，

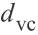
是带有值的自由分布：通过不利用结构和数据样本的分布，该界限会趋向于松弛。对于数据点是线性分开的，包含半径为R，两个非常接近点之间的边缘ρ，可以证明得到针对假设分类器有：

这就是支持向量机（SVM）背后的理论依据。

一个不等式去管理所有的它们

上面的所有分析是针对二元分类问题，然而VC的概念上的框架一般也适用于多分类与回归问题。根据相关研究人员的工作，不管这些工作产生的界限是多么的精确，总会有如下的形式:

其中C是假设空间复杂度、数据集大小以及置信度δ的函数，这个不等式基本说明泛化误差能够分解为两部分：经验训练误差和学习模型的复杂度。该不等式的形式对于任何学习问题、不管多么准确界限而言都是适用的。

参考文献：

l Mohri, Mehryar, Afshin Rostamizadeh, and Ameet Talwalkar. Foundations of machine learning. MIT press, 2012.

l Shalev-Shwartz, Shai, and Shai Ben-David. Understanding machine learning: From theory to algorithms. Cambridge University Press, 2014.

l Abu-Mostafa, Y. S., Magdon-Ismail, M., & Lin, H. (2012). Learning from data: a short course.

文章原标题《Machine Learning Theory - Part II》，作者：Mostafa Samir，译者：海棠

文章为简译，更为详细的内容，请查看原文

————————————————————————————————

三、《机器学习理论三部曲》——正则化和偏置方差的权衡 (Part III )

本文由北邮@爱可可-爱生活老师推荐，阿里云云栖社区组织翻译。

以下为译文

机器学习理论-Part3 正则化和偏置方差的权衡

在第一部分探讨了统计模型潜在的机器学习问题，并用它公式化获得最小泛化误差这一问题；在第二部分通过建立关于难懂的泛化误差的理论去得到实际能够估计得到的经验误差，最后的结果是：

通过假设有固定的数据集，可以简化该界限，对于具体的置信度有：

本节基于该简化理论结果，开始针对解决机器学习问题的过程总结一些概念。

为什么丰富假设是坏的？

为了让事情更加具体并能够将讨论的内容可视化，将会使用仿真数据集。在仿真数据集中定义目标函数，使用该函数并通过计算机程序画出尽可能多想要的数据集。

接下来讨论统一来自区间[-1,1]之间样本x，并使用一维目标函数

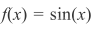
，加入零均值，标准差为2的高斯分布噪声后为

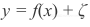
。由于想要预测特征和响应y之间的关系，需要假设噪声尽可能的小。

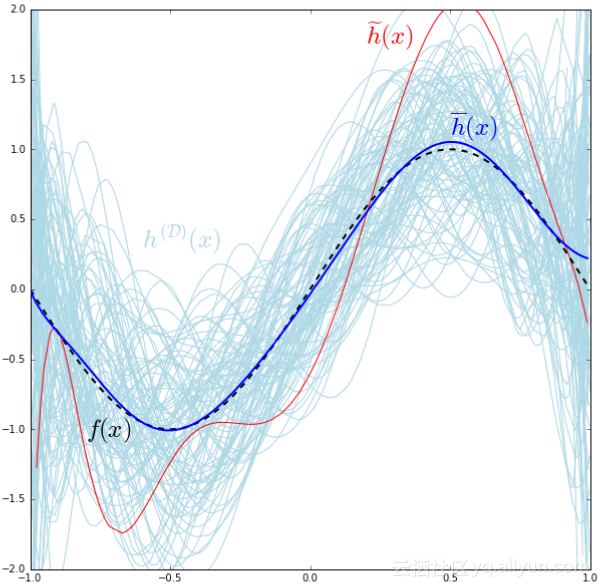
下面训练一个线性、三次和十次多项式假设，仿真样本集有200个点，画出以上描述的分布，这些模型用淡蓝色的线标注，假设的平均值是用黑色蓝线标注，然而真实值是用破折线表示。

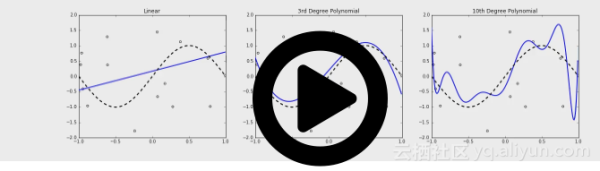
首先可以注意到越丰富，假设越复杂，真实目标的平均值也变得越小，估计的均值与目标值之间的差在统计学上作为偏差：

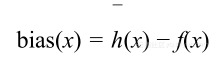
为了让解释更加具体，对目标函数进行泰勒展开，形式如下：

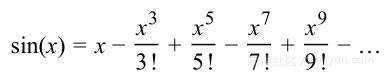
明显地，随着分母的增大，高分量对函数的贡献越小，这也导致更高分量显得次要。

线性模型的高偏置能够通过线性假设函数

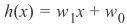
解释，目标函数的主要x分量为

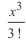
，同样地三次模型的低偏置能够通过三次假设函数

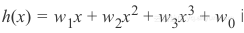
解释。

很容易看到，假设与目标的平均值越接近，从目标值得到的平均损失也越小。这意味着低偏置的假设结果有着低的经验风险。

假设越丰富，捕获噪声的能力也变得越大，回到刚才的动画，可以注意到三次模型是如何达到目标图表尖峰的，但在顶帧时仍然不能够得到，最后在十次模型能得到顶峰，这种假设被称为数据集的过拟合。过拟合的行为可以通过注意挤满在其均值（深蓝色曲线）周围的线性假设的实值（淡蓝色曲线）与凌乱的十次模型均值周围的对比来量化。这表明假设越过拟合，可能实值在其均值周围分散得越宽，所以假设过拟合能够通过均值周围的方差为多少量化：

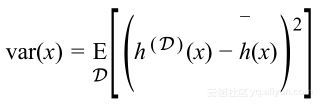
显然地，高方差模型不是理想的，因为我们不希望去适应噪声，因为丰富模型有更高的方差，这使得模型很坏并且泛化界限受到惩罚。

方差分解

下图是十次模型图：

由于

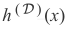
每次随着随机采样D而变化，考虑将

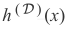
作为精确假设的随机变量。利用第一部分中的类似技巧，将随机变量分解成两个分量：代表其均值的确定性分量和代表其方差的随机分量；

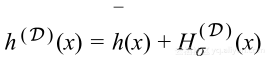
其中

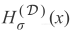
是零均值、方差等于假设方差的随机变量：

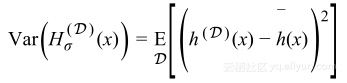
因此

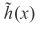
可以用

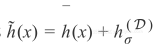
表示。

使用损失函数的平方差，能够对一些具体数据点x的风险写成：

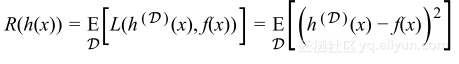
用数据集D的期望作为数据点(x,y)分布的期望，使用

的分解值可以得到：

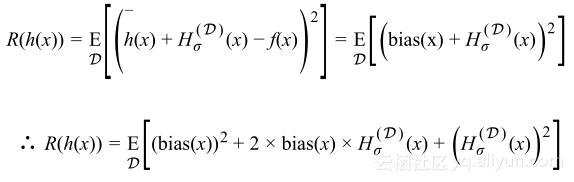
由于期望的线性性和偏置不依赖D的事实，重写上述等式：

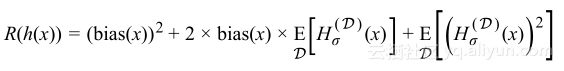
由于

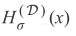
的均值为0，且有

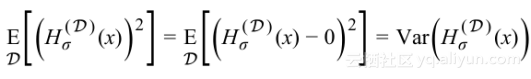
则有

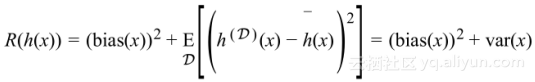
对于每个可能数据集D的所有数据点，其风险是

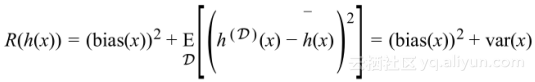
这表明泛化误差很好地分解为模型的偏置和方差，将这分解与泛化不等式相比，可以看到偏置与经验风险、方差与复杂性术语之间的联系。这就是偏置-方差分解，需要找到偏置与方差之间平衡的模型。

改良丰富度

研究更多的过拟合行为，考虑个体假设，关注红色曲线

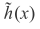
并查看其多项式系数，特别是对于目标函数的泰勒展开而言，对于特定函数，我们研究后发现：

1. 它的x前系数是3.9，而不是目标函数泰勒展开中的1；

2. 它的

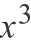
前系数为-5.4，而不是

；

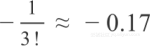
3. 它的

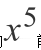
前系数为22.7，而不是

；

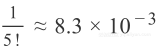
4. 它的

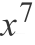
前系数为-53.1，而不是

；

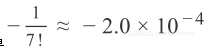
5. 它的

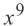
前系数为33.0，而不是

；

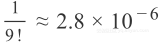
可以看到，假设大大过估计了其系数，因此给了另外一种方法量化过拟合行为，即该假设的参数或者系数的大小是否大于其真值。

在训练模型时，发现参数w向量最小化给定数据集的经验风险，表示为优化问题：

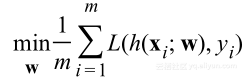
其中m是数据集大小，x是特征向量，h(x;w)是假设。为了最小化幅度值，等价于队每个幅度进行范数约束，选择其中的一种欧几里得范数：

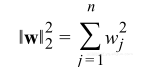
N表示特征的数量，所以我们能够重写最优化约束为：

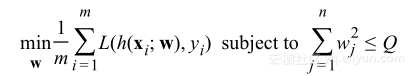
引入拉格朗日乘子，可以以无约束方式表述约束最优化问题：

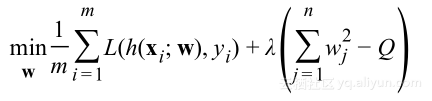
通过选择λ约束Q，可以摆脱对Q的显著依赖，并使用任意常数k替换Q：

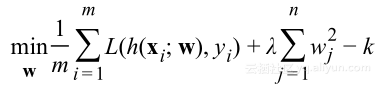
上式就是正则化损失函数，这种正则化形式由于使用的是L2范数，也被称为L2-正则化。

上图显示的是L2正则化训练十次模型的结果，可以看到正则化结果无正则化的效果要好；尽管正则化使得偏置增大，但其方差降低得更多，这使得整体风险变小。

下图显示的是线性模型的均方差损失的轮廓，红色曲线描述的是L2正则化约束

。

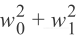
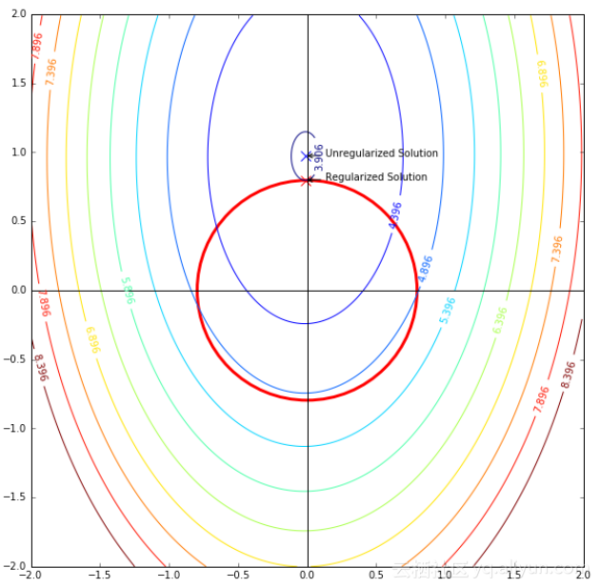
该图表明当使用正则化后，最优化问题的解决方案从原始位置移动到该约束圆的最低位置，这意味着对于可行的解决方案，必须在该约束圆内，所以考虑将整个2维图表作为正则化前的假设空间，正则化后将假设空间约束到红圈中。

有着上述观察，可以将最小化问题

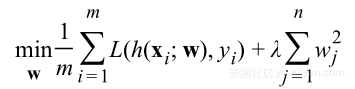
等价于泛化界限

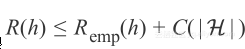
，正则项作为复杂项的最小值，这种变换的唯一缺少的是损失函数L的定义，这里使用的是平方差，下次将选择其他的损失函数并结合其所有的基本原则。

参考文献：

l Christopher M. Bishop. 2006. Pattern Recognition and Machine Learning (Information Science and Statistics). Springer-Verlag New York, Inc., Secaucus, NJ, USA.

l Abu-Mostafa, Y. S., Magdon-Ismail, M., & Lin, H. (2012). Learning from data: ashort course.

文章原标题《Machine Learning Theory - Part III》，作者：Mostafa Samir，译者：海棠

文章为简译，更为详细的内容，请查看原文

转载于:https://my.oschina.net/u/3579120/blog/1533192