
图片:我自己画的当某个人被打出太空时的草图
超人十分强壮,以至于他能做任何事情,对吗?那么他能够用力去揍一个人最后使那个人飞到太空吗?让我们来探讨一下吧。
太空距离我们有多远?
当我提起太空(space)时,你会认为我指的是“外太空”。但是太空有多高呢?地球的大气层不仅仅就停留在某些高度。不,与之相反,随着高度的上升空气的密度会随之降低,直到你甚至没有办法检测到空气为止。但是对于这个问题,我们必须选择一个高度。我现在要将高于地球表面420千米的空间定义为“太空”。也许你会问为什么?但为什么不呢?这大概就是国际宇宙空间站所在轨道的高度,所以我认为这个是一个很好的选择。
被打的那个人速度需要达到多快?
我是指被超人揍了之后的速度。让我们先来看看一个人运动的初速度v0。如果这是在物理概论课程里的一道题的话,我希望你考虑一下动能定理。
我们假设被超人打的那个人是他的克隆人,称之为超人-b,当然只是举个例子。如果我将超人-b和地球作为一个系统,然后除开超人对超人-b做的功外系统中就没有其他外力做功,那么能量的变化就有两种,动能和重力势能。

我知道这些变量的大小。如果我带入我知道的数值,那么我就会得出一个2778米每秒(6214英里每小时)的发射速度。是的,这很快,但实际上超人-b的速度需要更快。这是为什么呢?空气阻力就是原因。
在空气阻力存在下的发射速度
以下是超人-b在被超人打飞后的受力分析:

我会用下面两个公式来计算地球重力和空气阻力的大小。

对于重力,M和m分别代表地球的质量和超人-b的质量,r是超人-b与地心的距离。当超人-b离太空越来越近时,重力的大小就会减小。
对于空气阻力,A是指物体的迎风面积,C是由物体形状计算出的空气阻力系数。ρ是空气密度,当你离地面越高,空气密度就越小。所以,可以看出空气阻力会随着速度以及高度的变化而变化。实际上,空气阻力系数也取决于速度,但是在这里我们把它当做常数。所以,这不是一个这么简单的问题。
让我们对一些数值进行估计。我假设超人-b与普通人有着一样的体型。也许他的质量是70kg。对于AC的大小,我们需要基于跳伞运动员的极限速度来估计。如果一个跳伞运动员下降的极限速度为120英里每小时(54米每秒),那么空气阻力就会等于跳伞运动员的重力。也就是说AC等于:
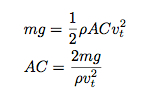
因为跳伞运动员的极限速度实在接近地球表面时达到的,所以我能用mg来近似作为他的重力。同理,我们也可以用1.2kg/m3来作为空气密度。将这些数值带入我们可以得出AC的大小大概为0.392 m2。但是我会恰好取0.05 m2作为AC的值。这又是为什么呢?因为之前的计算是基于一个处于典型跳伞运动的跳伞运动员。如果超人-b是以头朝上的方式“发射”出去,那么他会有一个小很多的迎风面积。也许会太小,但是这是可以的。
还有一个问题就是我们必须处理持续变化的空气阻力。走运的是,我以前曾经看过在高海拔的空气阻力的数据。是的,红牛最高太空降落项目(Red Bull Stratos Space Jump)就是从一个空气密度远远低于地球表面的一个点开始的。在下降速度的计算过程中,我用了如下这个空气密度的模型。
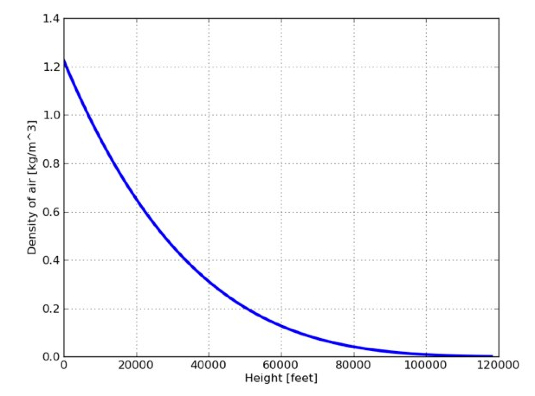
这个模型并不完全适用于极其高的海拔。所以我只在100km以下使用这个模型,在更高的高度我们假设空气密度是可以忽略不计的。是的,我知道这样不对,但是对于这个问题来说还是可行的。首先,我会尝试去展现超人-b超级快的初始速度。将高空中的空气密度忽略会降低初速度需要达到的大小。同时,当超人-b到达那么高的高空时,他不会运动那么快了,此时空气阻力也会变得很小,尽管我还假设在那儿有一些空气。
那么现在呢?我还是无法直接计算出我们所需的初速度。但是我可以选择一些初速度并且创造一个数字模型,来看在这些速度下超人-b达到的高度。然后我可以一直增加我选择的初速度的大小直到我得到想要的高度。对于挑选的每一个初速度,我会将运动以很短的时间进行划分。在每一小段划分的运动中,我会做如下的事情(这些就是数值计算的基础原则basic principles of a numerical calculation):
- 计算每个高度的空气密度
- 用高度、空气密度以及当时的速度来计算出重力和空气阻力
- 根据力的大小,计算出在这一小段时间内动量的变化
- 根据动量,计算出在这一小段时间内高度的变化

我们可以看出,在这一个问题中,超人-b并没有达到420km。甚至没有接近。现在我们只需要保持增长发射速度直到到达我们所需要的速度。以下是一个初始速度(最高 105 m/s)与能够达到最高高度的函数的图像。

尽管在 105 m/s这个速度,超人-b也只能够达到13km这个高度。这个结果让我有些失望。我原先以为我可以让超人-b飞得再更高一些。但是如果我在海拔为8.5km的珠穆朗玛峰上来解决这个问题呢?如果是这样,空气密度会更低,也许我会达到更高的高度。
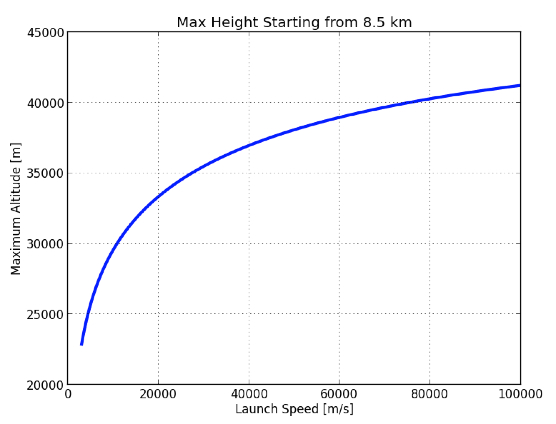
这样好一些了,但是依旧没有达到外太空。好吧,我们只是说超人一拳击飞了超人-b,并使超人-b有了初速度(在被打了后速度变为105 m/s),但是超人-b依旧没有飞出太空。他只是到了很高的地方。他能进入外太空吗?至少用我的空气阻力模型是不行的。也许有一种方法可以,但绝对不是我这种方法。
那么超人的那一记重拳打击呢?
好吧,我们说超人打超人-b那一拳确实十分用力。用力到超人-b能够达到105 m/s的速度。那么会发生什么?我们假设那一拳正中下巴,一记上勾拳。这是超人-b在接受那一拳时的受力分析。
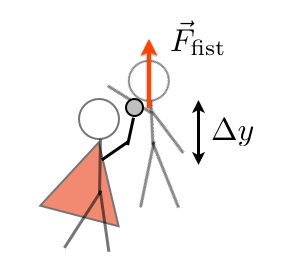
在这里,超人-b在经历了Δy的距离后,由初速度为零达到了的105m/s速度。超人的力要多大才能达到这个速度呢?我会忽视重力(真的,在这个例子里,重力的影响实在太小),然后使用动能定理。如果超人-b是受力物体,那么只有超人在做功。
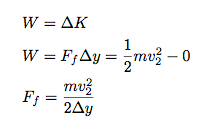
这就是超人-b所承受的来自超人拳头的力的平均大小。我唯一没有顾忌的就是在承受拳击后超人-b移动的距离。我认为0.75米会是一个适宜的估计。以此,可以计算出力的平均大小是4.67 x 1011牛。
假设超人的拳头与下巴的接触面积为70平方厘米(我是用我自己的拳头的截面来做的估计的,当然我将超人的拳头放大了些)。那么在这一拳中超人-b的皮肤承受了多大的压力呢?

这真是一个很大的数字。一个水中呼吸氧气筒的压力为3000磅每平方英寸,而它的钢罐却有四分之一英尺的厚度。我想表达什么?我只是在想超人能否如此用力的击打超人-b?我认为他的拳头会直接打爆超人-b的头。我知道,显而易见。
那么超人的脚与地面的接触面又承受着怎样的压力呢?超人向下对地面的力的大小大致等同于他对超人-b的作用力。当然,他的脚与地面的接触面积可能要更大一些,但是压力依旧是巨大的。我十分肯定他会被自己击出的那一拳反作用推入地里。
超人-b又怎么了呢?
如果超人-b的质量为70kg,那么我就可以得出在这一拳中他的平均加速度,就是用力除以他的质量(同上,重力相比起来是很小的)。他的平均加速度会达到6.67 x 109 m/s2。
不如假设超人-b是由两部分组成的。他的脑袋质量为7kg,他身体的其他部分质量则为63kg。超人正好打到超人-b的脑袋上。那么为什么超人-b剩下的部分也会加速呢?当然,他的脑袋与他的身体是联系在一起的。也就是说超人-b的脑袋用脖子拉着他的身体。为了使他的身体达到与脑袋相同的加速度,必须要有一个大小为4.2 x 1011 牛的力。
一艘尼米兹号级的航空母舰的质量大概为 9 x 107 kg。为了能产生于超人的脖子承受的力的大小一样的力,你需要将把他挂起来然后将4500艘航空母舰挂在他的脖子上。我不知道你是怎样的,但我认为他的脑袋会掉下来(况且全世界也没有4500艘这么大的航空母舰)。
回到最初的问题。超人能一拳把某个人打上太空吗?答案是不能,原因如下。
- 如果你计算空气阻力,你的初速度越高空气阻力就越大。而这是不可能发生的。
- 就算超人确实十分用力的击打某个人,超人的拳头也很可能会打穿目标的脑袋。
- 如果如此用力的打某个人,超人的脚也会直接陷入地面。
- 被击中的人的加速度实在太大以至于他的脑袋会与身体分离。
当然,我知道,超人不是真实存在的。我只是很期待在这篇文章发出后网上激烈的争论而已。
本译文仅用于学习和交流目的。非商业转载请注明译者、出处,并保留文章在译言的完整链接。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








