转自:1、http://blog.csdn.net/zouxy09/article/details/16955347
2、http://www.zhizhihu.com/html/y2010/2202.html
一、kNN算法分析
K最近邻(k-Nearest Neighbor,KNN)分类算法可以说是最简单的机器学习算法了。它采用测量不同特征值之间的距离方法进行分类。它的思想很简单:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
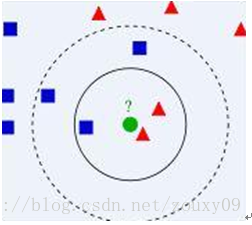
比如上面这个图,我们有两类数据,分别是蓝色方块和红色三角形,他们分布在一个上图的二维中间中。那么假如我们有一个绿色圆圈这个数据,需要判断这个数据是属于蓝色方块这一类,还是与红色三角形同类。怎么做呢?我们先把离这个绿色圆圈最近的几个点找到,因为我们觉得离绿色圆圈最近的才对它的类别有判断的帮助。那到底要用多少个来判断呢?这个个数就是k了。如果k=3,就表示我们选择离绿色圆圈最近的3个点来判断,由于红色三角形所占比例为2/3,所以我们认为绿色圆是和红色三角形同类。如果k=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。从这里可以看到,k的值还是很重要的。
KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
该算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。因此可以采用权值的方法(和该样本距离小的邻居权值大)来改进。该方法的另一个不足之处是计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分[参考机器学习十大算法]。
总的来说就是我们已经存在了一个带标签的数据库,然后输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似(最近邻)的分类标签。一般来说,只选择样本数据库中前k个最相似的数据。最后,选择k个最相似数据中出现次数最多的分类。其算法描述如下:
1)计算已知类别数据集中的点与当前点之间的距离;
2)按照距离递增次序排序;
3)选取与当前点距离最小的k个点;
4)确定前k个点所在类别的出现频率;
5)返回前k个点出现频率最高的类别作为当前点的预测分类。
***********************************************************************************************************************************************************************************
K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。该方法的思路是:如果一个样本在特征空间中的k个最相 似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决 策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN方法虽然从原理上也依赖于极限定理,但在类别决策时,只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方 法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
其 中,x为一篇待分类网页的向量表示;di为训练集中的一篇实例网页的向量表示;cj为一类别;(当d属于c}1,0{),(∈jicdyj时取1;当不属 于cdj时取0);bj为预先计算得到的cj的最优截尾阈值;为待分类网页与网页实例之间的相似度,由文档间的余弦相似度公式(11-10)计算得到:
kNN算法本身简单有效,它是一种lazy-learning算法,分类器不需要使用训练集进行训练,训练时间复杂度为0。kNN分类的计算复杂度和训练集中的文档数目成正比,也就是说,如果训练集中文档总数为n,那么kNN的分类时间复杂度为O(n)。
KNN算法不仅可以用于分类,还可以用于回归。通过找出一个样本的k个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight),如权值与距离成正比。
该算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的 K个邻居中大容量类的样本占多数。因此可以采用权值的方法(和该样本距离小的邻居权值大)来改进。该方法的另一个不足之处是计算量较大,因为对每一个待分 类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。该 算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
二、matlab实现
% cvKnnDemo - Demo of cvKnn.m
function cvKnnDemo
trainData = [
0.6213 0.5226 0.9797 0.9568 0.8801 0.8757 0.1730 0.2714 0.2523
0.7373 0.8939 0.6614 0.0118 0.1991 0.0648 0.2987 0.2844 0.4692
];
trainClass = [
1 1 1 2 2 2 3 3 3
];
testData = [
0.9883 0.5828 0.4235 0.5155 0.3340
0.4329 0.2259 0.5798 0.7604 0.5298
];
% main
testClass = cvKnn(testData, trainData, trainClass);
% plot prototype vectors
classLabel = unique(trainClass);
nClass = length(classLabel);
plotLabel = {'r*', 'g*', 'b*'};
figure;
for i=1:nClass
A = trainData(:, trainClass == classLabel(i));
plot(A(1,:), A(2,:), plotLabel{i});
hold on;
end
% plot classifiee vectors
plotLabel = {'ro', 'go', 'bo'};
for i=1:nClass
A = testData(:, testClass == classLabel(i));
plot(A(1,:), A(2,:), plotLabel{i});
hold on;
end
legend('1: prototype','2: prototype', '3: prototype', '1: classifiee', '2: classifiee', '3: classifiee', 'Location', 'NorthWest');
title('K nearest neighbor');
hold off;cvKnn
% cvKnn - K-Nearest Neighbor classification
%
% Synopsis
% [Class] = cvKnn(X, Proto, ProtoClass, [K], [distFunc])
%
% Description
% K-Nearest Neighbor classification
%
% Inputs ([]s are optional)
% (matrix) X D x N matrix representing column classifiee vectors
% where D is the number of dimensions and N is the
% number of vectors.
% (matrix) Proto D x P matrix representing column prototype vectors
% where D is the number of dimensions and P is the
% number of vectors.
% (vector) ProtoClass
% 1 x P vector containing class lables for prototype
% vectors.
% (scalar) [K = 1] K-NN's K. Search K nearest neighbors.
% (func) [distFunc = @cvEucdist]
% A function handle for distance measure. The function
% must have two arguments for matrix X and Y. See
% cvEucdist.m (Euclidean distance) as a reference.
%
% Outputs ([]s are optional)
% (vector) Class 1 x N vector containing classified class labels
% for X. Class(n) is the class id for X(:,n).
% (matrix) [Rank] Available only for NN (K = 1) now.
% nClass x N vector containing ranking class labels
% for X. Rank(1,n) is the 1st candidate which is
% the same with Class(n), Rank(2,n) is the 2nd
% candidate, Rank(3,n) is the 3rd, and so on.
%
% See also
% cvEucdist, cvMahaldist
% Authors
% Naotoshi Seo <sonots(at)sonots.com>
%
% License
% The program is free to use for non-commercial academic purposes,
% but for course works, you must understand what is going inside to use.
% The program can be used, modified, or re-distributed for any purposes
% if you or one of your group understand codes (the one must come to
% court if court cases occur.) Please contact the authors if you are
% interested in using the program without meeting the above conditions.
%
% Changes
% 04/01/2005 First Edition
function [Class, Rank] = cvKnn(X, Proto, ProtoClass, K, distFunc)
if ~exist('K', 'var') || isempty(K)
K = 1;
end
if ~exist('distFunc', 'var') || isempty(distFunc)
distFunc = @cvEucdist;
end
if size(X, 1) ~= size(Proto, 1)
error('Dimensions of classifiee vectors and prototype vectors do not match.');
end
[~, N] = size(X);
% Calculate euclidean distances between classifiees and prototypes
d = distFunc(X, Proto);
if K == 1, % sort distances only if K>1
[mini, IndexProto] = min(d, [], 2); % 2 == row
Class = ProtoClass(IndexProto);
if nargout == 2, % instance indices in similarity descending order
[sorted, ind] = sort(d'); % PxN
RankIndex = ProtoClass(ind); %,e.g., [2 1 2 3 1 5 4 1 2]'
% conv into, e.g., [2 1 3 5 4]'
for n = 1:N
[ClassLabel, ind] = unique(RankIndex(:,n),'first');
[sorted, ind] = sort(ind);
Rank(:,n) = ClassLabel(ind);
end
end
else
[sorted, IndexProto] = sort(d'); % PxN
% K closest
IndexProto = IndexProto(1:K,:);
KnnClass = ProtoClass(IndexProto);
% Find all class labels
ClassLabel = unique(ProtoClass);
nClass = length(ClassLabel);
for i = 1:nClass
ClassCounter(i,:) = sum(KnnClass == ClassLabel(i));
end
[maxi, winnerLabelIndex] = max(ClassCounter, [], 1); % 1 == col
% Future Work: Handle ties somehow
Class = ClassLabel(winnerLabelIndex);
endcvEucdist
% cvEucdist - Euclidean distance
%
% Synopsis
% [d] = cvEucdist(X, Y)
%
% Description
% cvEucdist calculates a squared euclidean distance between X and Y.
%
% Inputs ([]s are optional)
% (matrix) X D x N matrix where D is the dimension of vectors
% and N is the number of vectors.
% (matrix) [Y] D x P matrix where D is the dimension of vectors
% and P is the number of vectors.
% If Y is not given, the L2 norm of X is computed and
% 1 x N matrix (not N x 1) is returned.
%
% Outputs ([]s are optional)
% (matrix) d N x P matrix where d(n,p) represents the squared
% euclidean distance between X(:,n) and Y(:,p).
%
% Examples
% X = [1 2
% 1 2];
% Y = [1 2 3
% 1 2 3];
% d = cvEucdist(X, Y)
% % 0 2 8
% % 2 0 2
%
% See also
% cvMahaldist
% Authors
% Naotoshi Seo <sonots(at)sonots.com>
%
% License
% The program is free to use for non-commercial academic purposes,
% but for course works, you must understand what is going inside to use.
% The program can be used, modified, or re-distributed for any purposes
% if you or one of your group understand codes (the one must come to
% court if court cases occur.) Please contact the authors if you are
% interested in using the program without meeting the above conditions.
%
% Changes
% 06/2006 First Edition
function d = cvEucdist(X, Y)
if ~exist('Y', 'var') || isempty(Y)
%% Y = zeros(size(X, 1), 1);
U = ones(size(X, 1), 1);
d = abs(X'.^2*U).'; return;
end
V = ~isnan(X); X(~V) = 0; % V = ones(D, N);
U = ~isnan(Y); Y(~U) = 0; % U = ones(D, P);
d = abs(X'.^2*U - 2*X'*Y + V'*Y.^2);






















 438
438

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








