最大子列和问题（分治法和在线处理）

    时间复杂度太大，该算法不可取。

    

    该时间复杂度为O(N)，一般遇到为次复杂度的可以考虑改进算法，使其复杂度为O(logN)，将会有大的改善。

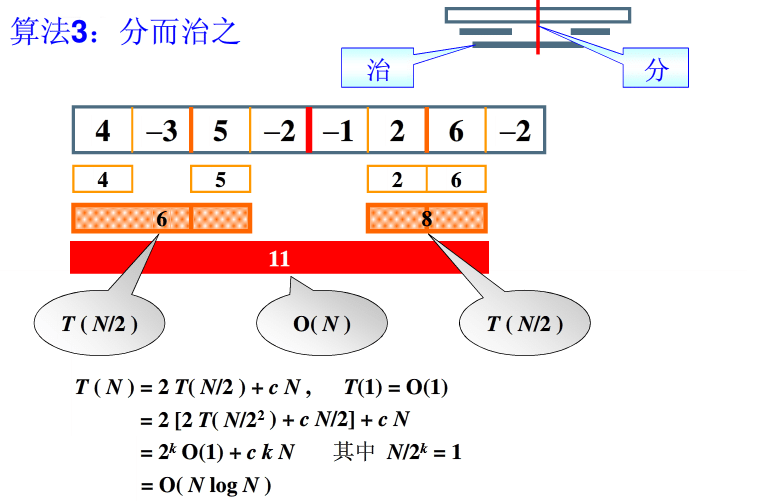
分治法在每一层递归上都有三个步骤：

分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；

解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题；

合并：将各个子问题的解合并为原问题的解。

针对此问题，分析方法如下：

1、先一分为二：左边为4，-3，5，-2；右边为：-1，2，6，-2

2、对左边再一分为二：左边为4，-3；右边为5，-2。计算左边子序列大于0的值分别为4和1，取4；计算右边子序列大于0的值分别为5和3，取5

3、对左边（4，-3，5，-2）再进行合：连续子序列跨越分界线计算的大于0的值为4-3+5=6最大，再与4和5相比较，得出6为最大值。

4、对右边再一分为二：左边为-1，2；右边为6，-2。计算左边子序列大于0的值分别为2和1，取2；计算右边子序列大于0的值分别为6和4，取6

5、对右边（-1，2，6，-2）再进行合：连续子序列跨越分界线计算的大于0的值为2+6=8最大，再与2和6比较，得出8为最大值。

6、对整个序列（4，-3，5，-2，-1，2，6，-2）进行合：连续子序列跨越分界线计算的大于0的值为4-3+5-2-1+2+6=11最大，再与6和8比较，得出11最大。

7、整个序列采用先分再合逐步递归的方法得出最终结果为11

时间复杂度为上图已经给出的O(NlogN)，针对本题，分治法依然不是最理想的算法。

在线处理的算法时间复杂度仅为O(N)，是最好的算法。

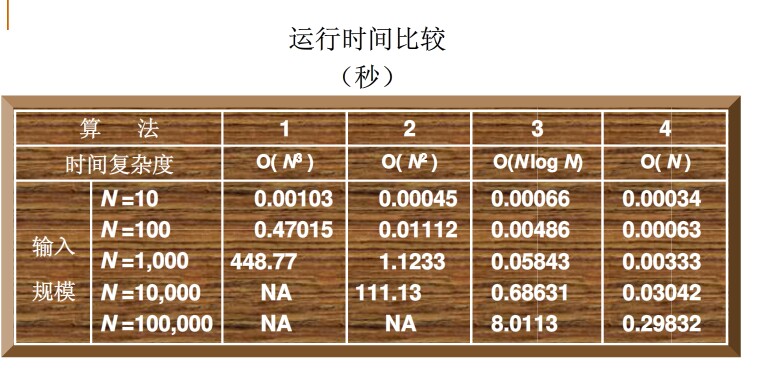
上图是以上四种算法运行时间进行比较，明显可以看出第四种算法最为高效。

上述各程序代码如下：

1. #include <stdio.h>
2. #include <time.h>
3. //算法1
4. int MaxSubseqSum1(int A[], int N, int * s, int* e)
5. {
6. int ThisSum, MaxSum = 0;
7. int i, j, k;
8. for (i = 0; i < N; i++) /* i是子列左端位置 */
9. { 
10. for (j = i; j < N; j++) /* j是子列右端位置 */
11. {
12. ThisSum = 0; /* ThisSum是从A[i]到A[j]的子列和 */
13. for (k = i; k <= j; k++) 
14. {
15. ThisSum += A[k];
16. }
17. if (ThisSum > MaxSum) /* 如果刚得到的这个子列和更大 */
18. {
19. MaxSum = ThisSum; /* 则更新结果 */
20. *e = j;
21. *s = i;
22. }
23. } /* j循环结束 */
24. } /* i循环结束 */
25. return MaxSum;
26. }
27. //算法2
28. int MaxSubseqSum2(int A[], int N,int * s, int* e)
29. {
30. int ThisSum, MaxSum = 0;
31. int i, j;
32. *s = 0;
33. *e = N;
34. for (i = 0; i < N; i++) /* i是子列左端位置 */
35. { 
36. ThisSum = 0; /* ThisSum是从A[i]到A[j]的子列和 */
37. for (j = i; j < N; j++) /* j是子列右端位置 */
38. { 
39. ThisSum += A[j];        /*对于相同的i，不同的j，只要在j-1次循环的基础上累加1项即可*/
40. if (ThisSum > MaxSum)   /* 如果刚得到的这个子列和更大 */
41. {
42. MaxSum = ThisSum;   /* 则更新结果 */
43. *e = j;
44. *s = i;
45. }
46. } /* j循环结束 */
47. } /* i循环结束 */
48. return MaxSum;
49. }
50. //算法3
51. int MaxSubseqSum3(int A[], int left, int right, int *s, int *e)
52. {
53. int i = 0, j = 0, sum = 0;
54. int s1 = 0, s2 = 0, lefts = 0, rights = 0;
55. int center, leftsum, rightsum;
56. if (left == right)
57. {
58. if (A[left]>0)
59. sum = A[left];
60. else
61. sum = 0;
62. *s = left; *e = right;
63. }
64. else
65. {
66. center = (left + right) / 2;               //划分
67. leftsum = MaxSubseqSum3(A, left, center, s, e);       //对应情况1，递归求解
68. rightsum = MaxSubseqSum3(A, center + 1, right, s, e);      //对应情况2，递归求解
69. //求解s1
70. for (i = center; i >= left; i--)
71. {
72. lefts +=A[i];
73. if (lefts > s1) 
74. {
75. *s = i;
76. *e = center/2*2;   //不清楚为啥是这样的
77. s1 = lefts;
78. }
79. }
80. //再求解s2
81. for (j = center + 1; j <= right; j++)
82. {
83. rights = rights + A[j];
84. if (rights > s2) 
85. {
86. s2 = rights; 
87. *e = j;
88. *s = (center+1)/2*2; //依然不清楚
89. }
90. }
91. sum = s1 + s2;                //计算情况3的最大子段和
92. if (sum<leftsum)
93. sum = leftsum;
94. if (sum<rightsum)
95. sum = rightsum;
96. }
97. return sum;
98. }
99. 
    
100. 
     
101. int MaxSubseqSum4(int A[], int N, int * s, int* e)
102. {
103. int ThisSum, MaxSum;
104. int i;
105. int ss = 0;
106. ThisSum = MaxSum = 0;
107. for (i = 0; i < N; i++) 
108. {
109. ThisSum += A[i]; /* 向右累加 */
110. if (ThisSum > MaxSum)
111. {
112. MaxSum = ThisSum; /* 发现更大和则更新当前结果 */
113. *s = ss;
114. *e = i;
115. }
116. else if (ThisSum < 0) /* 如果当前子列和为负 */
117. {
118. ThisSum = 0; /* 则不可能使后面的部分和增大，抛弃之 */
119. ss = i+1;
120. }
121. }
122. return MaxSum;
123. }
124. int main() {
125. int a[] = { -10 ,1, 2, 3, 4, - 5, - 23, 3, 7, - 21 };
126. int result,s,e,i;
127. clock_t start, ended;
128. double duration;
129. const int COUNT = 100000;
131. start = clock();
132. for ( i = 0; i< COUNT; i++)
133. result = MaxSubseqSum1(a, sizeof(a) / sizeof(a[0]), &s, &e);
134. ended = clock();
135. duration = (double)(ended - start) / CLK_TCK;
136. printf("ticks1    = %lf\n",(double)(ended - start));
137. printf("duration1 = %lf\n", duration);
138. printf("start1=%d,ended1=%d result1 = %d\n", s,e,result);
140. start = clock();
141. for ( i = 0; i< COUNT; i++)
142. result = MaxSubseqSum2(a, sizeof(a) / sizeof(a[0]), &s, &e);
143. ended = clock();
144. duration = (double)(ended - start) / CLK_TCK;
145. printf("ticks2    = %lf\n", (double)(ended - start));
146. printf("duration2 = %lf\n", duration);
147. printf("start2=%d,ended2=%d result2 = %d\n", s, e, result);
149. start = clock();
150. for ( i = 0; i< COUNT; i++)
151. result = MaxSubseqSum3(a, 0, sizeof(a) / sizeof(a[0]), &s, &e);
152. ended = clock();
153. duration = (double)(ended - start) / CLK_TCK;
154. printf("ticks3    = %lf\n", (double)(ended - start));
155. printf("duration3 = %lf\n", duration);
156. printf("start3=%d,ended3=%d result3 = %d\n", s, e, result);
157. 
     
158. start = clock();
159. for ( i = 0; i< COUNT; i++)
160. result = MaxSubseqSum4(a, sizeof(a) / sizeof(a[0]), &s, &e);
161. ended = clock();
162. duration = (double)(ended - start) / CLK_TCK;
163. printf("ticks4    = %lf\n", (double)(ended - start));
164. printf("duration4 = %lf\n", duration);
165. printf("start4=%d,ended4=%d result4 = %d\n", s, e, result);
166. return 0;
167. }

程序运行结果如下（在VS2010环境下）：

可以看出算法1最差，算法4在线处理最好。

下图所示是在VC++6.0下的运行结果：

其中算法3因为采用递归算法，空间复杂度太大，运行结果出现了错误。