《具体数学》1.3递归(三)续

上一篇我们讲到了，算J(100)=73,我们接着下面继续搞点事情出来.

若从n开始，且重复作J函数m+1次，则我们作m+1次位的循环移动；由于n是一个(m+1)位的数，所以可期望最后再得出n。但事情并非真的是这样。例如，若n=13,则我们得到J((1101)2)=(1011)2,但是J((1011)2)=(111)2,且过程中止，当0变成第一位时，它消失了，事实上，由定义J(n)总是<=n,因为J(n)是幸存者的编号，因此若J(n)<n,连续重复，我们不可能倒转到n

重复应用J产生一系列下降值，最终达到一个指定点，在那里J(n)=n.循环移的性质使我们容易看出指定点是什么:重复函数足够多次将产生一个全为1的型式，它的值是2^v(n)-1,其中v(n)是n的二进制表示中1的位数。因此，由于v(13)=3,我们得到

2个或多于2个J

2个或多于2个J

J(J(...J(13)...))=2^3-1=7

类似

8个或多于8个

J(J(...J((101101101101011)2)...))=2^10-1=1023

难以理解，但是为真.大爱这句话!

好，让我们再看看添加什么条件能使最初的猜测成立：
当n为偶数时，满足J(n)=n/2
假设n = 2^m + l，那么我们由J(n) = n / 2，可以得到2l + 1 = (2^m + l) / 2，因此有：l = (2^m - 2) / 3。如果l = (2^m - 2) / 3是整数，那么n = 2^m + l就是解，因为l小于2^m。
可以验证，当m是奇数时，2^m - 2是3的倍数，而当m为偶数时则不是。因此方程J(n)=n/2有无限多个解：
n = 2^m + (2^m - 2) / 3 = (2^m+2  – 2) / 3 （m为奇数）

较小的解为

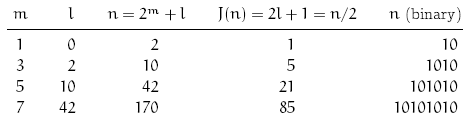
回顾一下，我们在二进制的帮助下解决了J函数，为什么级差非要为2，而不是3、4呢？OK，我们来推广一下，看看怎么消除“2”的特殊性。(从特殊到普遍)
直接从递归关系式开始。换成不同的常数系数，会怎样呢？
原来是
J(1) = 1
J(2n) = 2J(n) - 1
J(2n + 1) = 2J(n) + 1
我们换成
f(1) = α
f(2n) = 2f(n) + β
f(2n + 1) = 2f(n) + γ
从f(1) = α开始，并根据上面的方程逐步地推导，可以构造出较小n值上的函数值表：

我们可以看到什么结果？在n = 2m + l的情形下：1、α的系数是不大于n的最大的2的幂2m；
2、β和γ的系数都不大于2m ；
3、β的系数每次由2m -1递减直到0；
4、γ的系数每次递增直到2m - 1。
因此，f(n)可以表示成
f(n) = A(n) α + B(n) β + C(n) γ
这里有
A(n) = 2m
B(n) = 2m – l – 1
C(n) = l

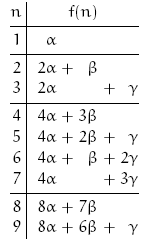
通过归纳法可以证明上面的式子，但是计算过程比较繁杂。我们尝试选择特定值，并将这些值组合在一起，看看能不能找到简单的证明方法。
考虑α = 1，β = γ =  0的特殊情况，此时f(n)的值与A(n)相等，递归方程变成：
A(1) = 1
A(2n) = 2A(n)
A(2n + 1) = 2A(n) = A(2n)                              
对上面的递归方程，我们很容易地得到：
A(2^m + l) = 2^m
Josephus问题的推广

反过来考虑。如果知道函数f(n)的封闭形式解，对应的常数组合(α, β, γ)是什么？
例如对于常数函数f (n) = 1有：
1 = α，1 = 2l + β，1 = 2l + γ 。
因此(α, β, γ) = (1, –1, –1)。此时f (n) = A(n)- B(n)- C(n) = 1。
再看函数f (n) = n：
1 = α，2n = 2n + β，2n + 1 = 2n + γ
因此(α, β, γ) = (1, 0, 1) 。特别是，我们不需要用归纳法证明即可知道f(n)的唯一解是f(n) = n。

回到我们在前面的问题：证明
A(n) = 2^m
B(n) = 2^m – l – 1
C(n) = l
现在我们已经知道函数A (n)，B (n)和C(n)满足：
1、从(α, β, γ) = (1, 0, 0) 得到：A(n) = 2^m 【f (n) = 2^m】
2、从(α, β, γ) = (1, -1, -1)得到：A(n) – B(n) – C(n) = 1【f(n) = 1】
3、从(α, β, γ) = (1, 0, 1)得到：A(n) + C(n) = n【f(n) = n】
解上述方程，可以得到
C(n) = n - A(n) = l，而B(n) = A(n) - 1 - C(n)= 2^m - l - 1
这与我们的猜想是一致的。

我们知道，原始的J函数有一个妙解，可用二进制表示为：
J(bmbm-1bm-2…b1b0)2 = (bm-1bm-2…b0bm)2
那么，广义Josephus递归方程是否也有这种奇妙的解呢？
当然是有的。如果我们令β0 = β而β1 =γ，那么可以将递归方程写成：
f(1) = α
f(2n+ j) = 2f(n) + βj

按二进制方式展开，此递归方程变成：
f((bmbm-1…b1b0)2) = 2f((bmbm-1…b1)2) + βb0
= 4f((bmbm-1…b2)2) + 2βb1 + βb0
……
= 2m f((bm)2) + 2m-1βbm-1+ … +2βb1 + βb0
= 2m α + 2m-1βbm-1+ … +2βb1 + βb0
接下来，放松二进制表示的限制，在每个位上允许使用任意数字，那么上面的结果可以表示成：
f((bmbm-1…b1b0)2) = (αβbm-1βbm-2 …… βb1βb0)2
看起来结果很完美。但是如果换一种方式来重写小数值n上的f(n)函数表的话，可能更容易发现这种规律：

f((bmbm-1…b1b0)2) = (αβbm-1βbm-2 …… βb1βb0)2
例如，当n = 100 = (1100100)2，在我们原来的Josephus参数α= 1，β = -1和γ = 1之下，可以得到

因为在n的表示中，每组二进制数字位 (10……00)2被转换为
 (1 -1 …… -1 -1)2 = (00……01)2
    这样就显示出了循环移位性质。

面我们进一步地进行一般化。来看递归方程
f(j) = αj
f(dn + j) = cf(n) + βj （j = 1……d）
这个递归方程的形式与前面基本相同，但是是以d进制的数开始，而且产生的值采用c进制来表示。
也就是说，它的自变量和函数值采用不同的基数来表示：
f((bmbm-1…b1b0)d) = (αbmβbm-1βbm-2 …… βb1βb0)c
例如，对于下面的递归方程，我们计算f(19)
f(1) = 34
f(2) = 5
f(3n) = 10f(n) + 76
f(3n + 1) = 10f(n) - 2
f(3n + 2) = 10f(n) + 8
也就是说d = 3，c = 10。因为19 = (201)3，为了使用变化基数的方法，我们逐位进行从基数3到基数10的转换：
第1位的2变成5，而0和1分别变成了76和 –2，因此结果为
f(19) = f((201)3) = (5.7.6.-2)10 = 1258
书上的最后讲的方法有点精髓，我看了好几遍的，才慢慢理解，估计是自己数学有点差劲了，哈哈，继续努力看下去，长春的天气是真的让你恼火。。。

转载于:https://my.oschina.net/u/1589875/blog/265758