哈希原理与常见哈希函数

一，什么是哈希

哈希是将任意长度的数据转换为一个数字的过程。这个数字是在一个固定的范围之内的。
转换的方法称为哈希函数，原值经过哈希函数计算后得到的值称为哈希值。

1.哈希特点

(1)一致性：同一个值每次经过同一个哈希函数计算后得到的哈希值是一致的。

F(x)=rand() :每次返回一个随机值,是不好的哈希

(2)散列性：不同的值的哈希值尽量不同，理想情况下每个值对应于不同的数字。

F(x)=1 : 不管输入什么都返回1，是不好的哈希

2.冲突怎么解决

把一个大的集合映射到一个固定大小的集合中，肯定是存在冲突的。这个是抽屉原理或者叫鸽巢理论。

桌上有十个苹果，要把这十个苹果放到九个抽屉里，无论怎样放，我们会发现至少会有一个抽屉里面放不少于两个苹果。这一现象就是我们所说的“抽屉原理”。 抽屉原理的一般含义为：“如果每个抽屉代表一个集合，每一个苹果就可以代表一个元素，假如有n+1个元素放到n个集合中去，其中必定有一个集合里至少有两个元素。” 抽屉原理有时也被称为鸽巢原理。它是组合数学中一个重要的原理。

（1）拉链法：

链表地址法是使用一个链表数组来存储相应数据，当hash遇到冲突的时候依次添加到链表的后面进行处理。Java里的HashMap是拉链法解决冲突的典型应用场景。

Java8的HashMap中，使用一个链表数组来存储数据，根据元素的哈希值确定存储的数组索引位置，当冲突时，就链接到元素后面形成一个链表，Java8中当链表长度超过8的时候就变成红黑树以优化性能，红黑树也可以视为拉链法的一种变形。

（2）开放地址法

开放地址法是指大小为 M 的数组保存 N 个键值对，其中 M >N。我们需要依靠数组中的空位解决碰撞冲突。基于这种策略的所有方法被统称为“开放地址”哈希表。

线性探测法，就是比较常用的一种“开放地址”哈希表的一种实现方式。线性探测法的核心思想是当冲突发生时，顺序查看表中下一单元，直到找出一个空单元或查遍全表。简单来说就是：一旦发生冲突，就去寻找下 一个空的散列表地址，只要散列表足够大，空的散列地址总能找到。

Java8中的HashTable就是用线性探测法来解决冲突的。

    public synchronized V put(K key, V value) {
        // Make sure the value is not null
        if (value == null) {
            throw new NullPointerException();
        }

        // Makes sure the key is not already in the hashtable.
        Entry<?,?> tab[] = table;
        int hash = key.hashCode();
        int index = (hash & 0x7FFFFFFF) % tab.length;
        @SuppressWarnings("unchecked")
        Entry<K,V> entry = (Entry<K,V>)tab[index];
        for(; entry != null ; entry = entry.next) {
            if ((entry.hash == hash) && entry.key.equals(key)) {
                V old = entry.value;
                entry.value = value;
                return old;
            }
        }

        addEntry(hash, key, value, index);
        return null;
    }

    private void addEntry(int hash, K key, V value, int index) {
        modCount++;

        Entry<?,?> tab[] = table;
        if (count >= threshold) {
            // Rehash the table if the threshold is exceeded
            rehash();

            tab = table;
            hash = key.hashCode();
            index = (hash & 0x7FFFFFFF) % tab.length;
        }

        // Creates the new entry.
        @SuppressWarnings("unchecked")
        Entry<K,V> e = (Entry<K,V>) tab[index];
        tab[index] = new Entry<>(hash, key, value, e);
        count++;
    }

（2）冲突解决示例

举个例子，假如散列长度为8，哈希函数是：y=x%7。两种解决冲突的方式如下：

拉链法解决冲突

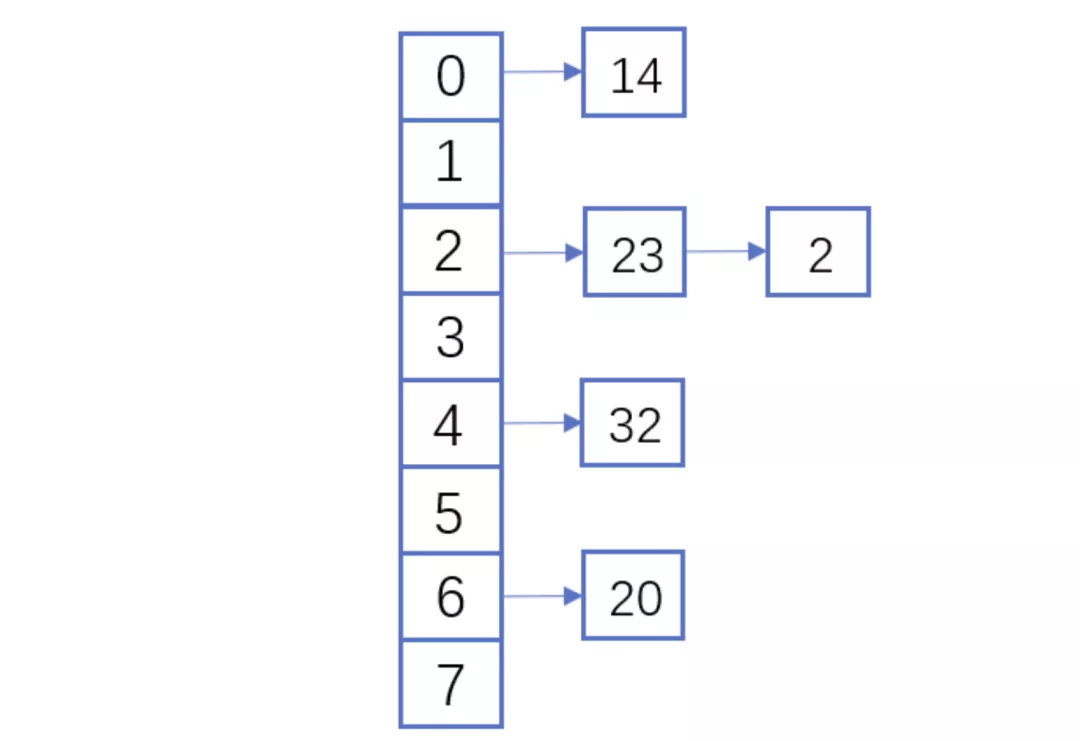
线性探测法解决冲突

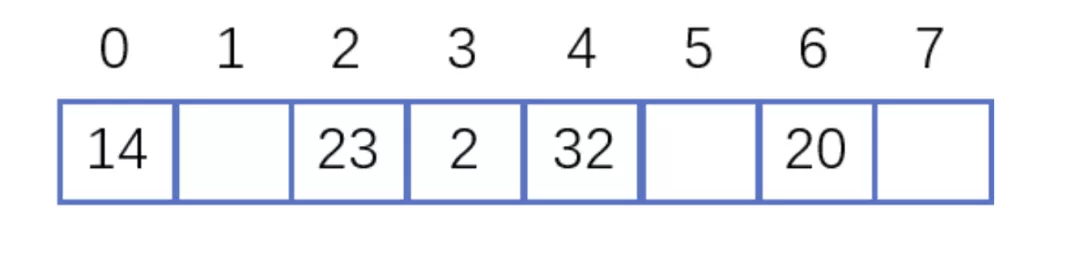
二，几个常见哈希算法

1.MD5

MD5哈希算法是将任意字符散列到一个长度为128位的Bit数组中，得出的结果表示为一个32位的十六进制数字。

MD5哈希算法有以下几个特点：

1. 正像快速：原始数据可以快速计算出哈希值
2. 逆向困难：通过哈希值基本不可能推导出原始数据
3. 输入敏感：原始数据只要有一点变动，得到的哈希值差别很大
4. 冲突避免：很难找到不同的原始数据得到相同的哈希值

算法过程：

1. 数据填充：

将原数据的二进制值进行补齐。

（1）填充数据：使得长度模除512后得到448，留出64个bit来存储原信息的长度。填充规则是填充一个1，后面全部是0。

（2）填充长度数据：计算原数据的长度数据，填充到最后的64个bit上，如果消息长度数据大于64bit就使用低64位的数据。

2. 迭代计算：

将填充好的数据按照每份512的长度进行切分，对每一份依次进行处理，每份的处理方式是使用四个函数进行依次进行计算，每个函数都有四个输入参数，输出也是四个数字，输出的数字作为下一份数据的输入，所有份数的数据处理完毕，得到的四个数字连接起来就是最终的MD5值。

以下图片是整个迭代计算的过程示意图，其中四个初始参数和四个函数定义如下：

//四个初始参数值
A=0x67452301;
B=0xefcdab89;
C=0x98badcfe;
D=0x10325476;

//四个函数的定义
// a、b、c、d是每次计算时候的四个参数
F=(b&c)|((~b)&d);
F=(d&b)|((~d)&c);
F=b^c^d;
F=c^(b|(~d));

3. md5的java实现

package com.chybin.algorithm.chapter2;

/**
 * Create By 鸣宇淳 on 2019/12/26
 **/
public class MD5{
    /*
     *四个链接变量
     */
    private final int A=0x67452301;
    private final int B=0xefcdab89;
    private final int C=0x98badcfe;
    private final int D=0x10325476;
    /*
     *ABCD的临时变量
     */
    private int Atemp,Btemp,Ctemp,Dtemp;

    /*
     *常量ti
     *公式:floor(abs(sin(i+1))×(2pow32)
     */
    private final int K[]={
            0xd76aa478,0xe8c7b756,0x242070db,0xc1bdceee,
            0xf57c0faf,0x4787c62a,0xa8304613,0xfd469501,0x698098d8,
            0x8b44f7af,0xffff5bb1,0x895cd7be,0x6b901122,0xfd987193,
            0xa679438e,0x49b40821,0xf61e2562,0xc040b340,0x265e5a51,
            0xe9b6c7aa,0xd62f105d,0x02441453,0xd8a1e681,0xe7d3fbc8,
            0x21e1cde6,0xc33707d6,0xf4d50d87,0x455a14ed,0xa9e3e905,
            0xfcefa3f8,0x676f02d9,0x8d2a4c8a,0xfffa3942,0x8771f681,
            0x6d9d6122,0xfde5380c,0xa4beea44,0x4bdecfa9,0xf6bb4b60,
            0xbebfbc70,0x289b7ec6,0xeaa127fa,0xd4ef3085,0x04881d05,
            0xd9d4d039,0xe6db99e5,0x1fa27cf8,0xc4ac5665,0xf4292244,
            0x432aff97,0xab9423a7,0xfc93a039,0x655b59c3,0x8f0ccc92,
            0xffeff47d,0x85845dd1,0x6fa87e4f,0xfe2ce6e0,0xa3014314,
            0x4e0811a1,0xf7537e82,0xbd3af235,0x2ad7d2bb,0xeb86d391};
    /*
     *向左位移数,计算方法未知
     */
    private final int s[]={7,12,17,22,7,12,17,22,7,12,17,22,7,
            12,17,22,5,9,14,20,5,9,14,20,5,9,14,20,5,9,14,20,
            4,11,16,23,4,11,16,23,4,11,16,23,4,11,16,23,6,10,
            15,21,6,10,15,21,6,10,15,21,6,10,15,21};


    /*
     *初始化函数
     */
    private void init(){
        Atemp=A;
        Btemp=B;
        Ctemp=C;
        Dtemp=D;
    }
    /*
     *移动一定位数
     */
    private    int    shift(int a,int s){
        return(a<<s)|(a>>>(32-s));//右移的时候，高位一定要补零，而不是补充符号位
    }
    /*
     *主循环
     */
    private void MainLoop(int M[]){
        int F,g;
        int a=Atemp;
        int b=Btemp;
        int c=Ctemp;
        int d=Dtemp;
        for(int i = 0; i < 64; i ++){
            if(i<16){
                F=(b&c)|((~b)&d);
                g=i;
            }else if(i<32){
                F=(d&b)|((~d)&c);
                g=(5*i+1)%16;
            }else if(i<48){
                F=b^c^d;
                g=(3*i+5)%16;
            }else{
                F=c^(b|(~d));
                g=(7*i)%16;
            }
            int tmp=d;
            d=c;
            c=b;
            b=b+shift(a+F+K[i]+M[g],s[i]);
            a=tmp;
        }
        Atemp=a+Atemp;
        Btemp=b+Btemp;
        Ctemp=c+Ctemp;
        Dtemp=d+Dtemp;

    }
    /*
     *填充函数
     *处理后应满足bits≡448(mod512),字节就是bytes≡56（mode64)
     *填充方式为先加一个0,其它位补零
     *最后加上64位的原来长度
     */
    private int[] add(String str){
        int num=((str.length()+8)/64)+1;//以512位，64个字节为一组
        int strByte[]=new int[num*16];//64/4=16，所以有16个整数
        for(int i=0;i<num*16;i++){//全部初始化0
            strByte[i]=0;
        }
        int    i;
        for(i=0;i<str.length();i++){
            strByte[i>>2]|=str.charAt(i)<<((i%4)*8);//一个整数存储四个字节，小端序
        }
        strByte[i>>2]|=0x80<<((i%4)*8);//尾部添加1
        /*
         *添加原长度，长度指位的长度，所以要乘8，然后是小端序，所以放在倒数第二个,这里长度只用了32位
         */
        strByte[num*16-2]=str.length()*8;
        return strByte;
    }
    /*
     *调用函数
     */
    public String getMD5(String source){
        init();
        int strByte[]=add(source);
        for(int i=0;i<strByte.length/16;i++){
            int num[]=new int[16];
            for(int j=0;j<16;j++){
                num[j]=strByte[i*16+j];
            }
            MainLoop(num);
        }
        return changeHex(Atemp)+changeHex(Btemp)+changeHex(Ctemp)+changeHex(Dtemp);

    }
    /*
     *整数变成16进制字符串
     */
    private String changeHex(int a){
        String str="";
        for(int i=0;i<4;i++){
            str+=String.format("%2s", Integer.toHexString(((a>>i*8)%(1<<8))&0xff)).replace(' ', '0');

        }
        return str;
    }
    /*
     *单例
     */
    private static MD5 instance;
    public static MD5 getInstance(){
        if(instance==null){
            instance=new MD5();
        }
        return instance;
    }

    private MD5(){};

    public static void main(String[] args){
        String str=MD5.getInstance().getMD5("123");
        System.out.println(str);
    }
}

2.SHA

SHA类似MD5，也是一种信息摘要算法，也是将任意长度的字符串转换为固定长度的数字的算法。SHA算法是一个家族，有五个算法：SHA-1、SHA-224、SHA-256、SHA-384，和SHA-512。这些变体除了生成摘要的长度、循环运行的次数等一些微小差异外，算法的基本结构是一致的。

SHA-1算法的结果是一个160个bit的数字，比MD5的128个bit要长32位，碰撞几率要低了2^32倍。可是SHA-1和MD5一样已经被人破解，已经不安全了。

SHA-256从名字上看就表明了它的值存储在长度为256的bit数组中的，SHA-512信息摘要长度是512个bit。

SHA-224是SHA256的精简版本，SHA-384是SHA-512的精简版本，精简版本主要用在安全等级要求不太高的场景，比如只是验证下文件的完整性。使用什么版本的SHA取决于安全要求和算法速度，毕竟长度越长算法计算时间约长，但是安全等级高。

SHA算法过程：

SHA算法的底层原理和MD5很相似，只是在摘要分段和处理细节上有少许差别，他们都是第一步将原数据进行填充，填充到512的整数倍，填充的信息包括10数据填充和长度填充，第二步切分为相同大小的块，第三步进行对每一块迭代，每块进行N轮运算，最终得到的值拼接起来就是最终的哈希值。

以下是MD5、SHA-1、SHA-2系列的算法过程比较：

MD5算法过程示意图：

MD5是对每一块数据分为四个部分，用四个函数进行运算。最终生成128位的哈希值。

SHA-1算法过程示意图：

SHA-1是将每一块数据分为五个部分。

SHA-2算法过程示意图：

SHA-2是分为八个部分，算法也更加复杂。

3.SimHash

SimHash是Google提出的一种判断文档是否重复的哈希算法，他是将文本转换为一个64位的哈希值，然后计算两个哈希值的距离，如果小于n（n一般是3）就认为这两个文本是相似的。

之所以能够这样判断是否相似是因为SimHash算法不同于MD5之类的算法，SimHash算法是局部敏感的哈希算法，MD5算法是全局敏感的哈希算法。在MD5中原数据只要有一个字符的变化，哈希值就会变化很大，而在SimHash算法中，原数据变化一小部分，哈希值也只有很小一部分的变化，所以只要哈希值很类似，就意味着原数据就很类似。

算法实现：

参考这个博客【[Algorithm] 使用SimHash进行海量文本去重】

（1）第一步：哈希

1. 分词： 将文本进行分词，并给单词分配权重。
2. hash： 对每个次进行hash计算，得到哈希值。
3. 加权： 对每个单词的has进行加权。
4. 合并： 把上一步加权hash值合并累计起来。
5. 降维： 把上一步累加起来的值变为01。如果每一位大于0 记为 1，小于0 记为 0。

（2）第二步：计算海明距离

两个simhash对应二进制（01串）取值不同的数量称为这两个simhash的海明距离。

举例如下： 10101 和 00110 从第一位开始依次有第一位、第四、第五位不同，则海明距离为3。

异或就是如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。两个simhash值进行异或，得出的结果中1的个数就是海明距离。

判断两个文本是否相似，就计算两个simhash哈希值的海明距离，根据经验，如果海明距离小于3就可以判定两个文本是相似的。

4.GeoHash

GeoHash 算法将经纬度哈希为一个数字，然后将数字base32编码为一个字符串。

比如：北海公园的经纬度是：(39.928167,116.389550),对应的GeoHash值可以为wx4g、wx4g0、wx4g0s、wx4g0s8、wx4g0s8q。GeoHash值代表的是这个经纬度点所在的一个矩形区域，长度越长矩形面积约小，表示的越精确。

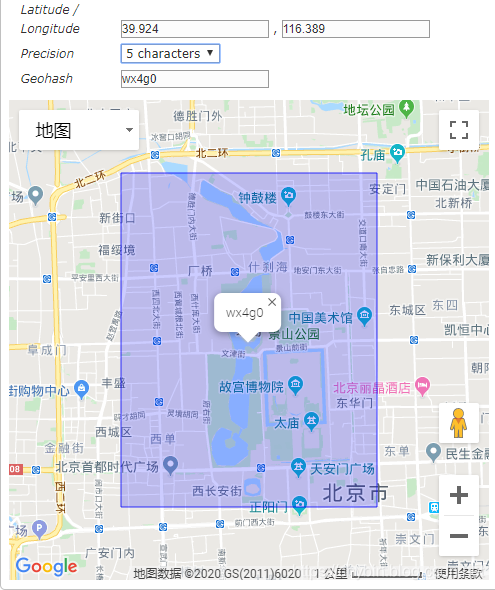
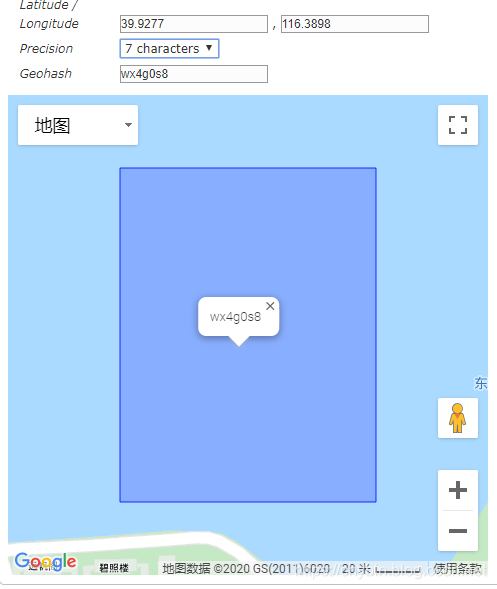
两个位置的GeoHash值前部分一样的位数越多，说明两个位置离得越近，百度地图的查找附近、滴滴打车查找附近的车辆功能就可以使用这个算法。

GeoHash算法过程

下面对于北海公园的经纬度(39.928167,116.389550)进行编码，了解下算法过程。

（1）第一步：纬度编码

将整个地球从水平方向上进行逐步切分，确定纬度39.928167在哪个区域中。

纬度范围是-90到90，每次平均分为两份，进行逐步细化地迭代。

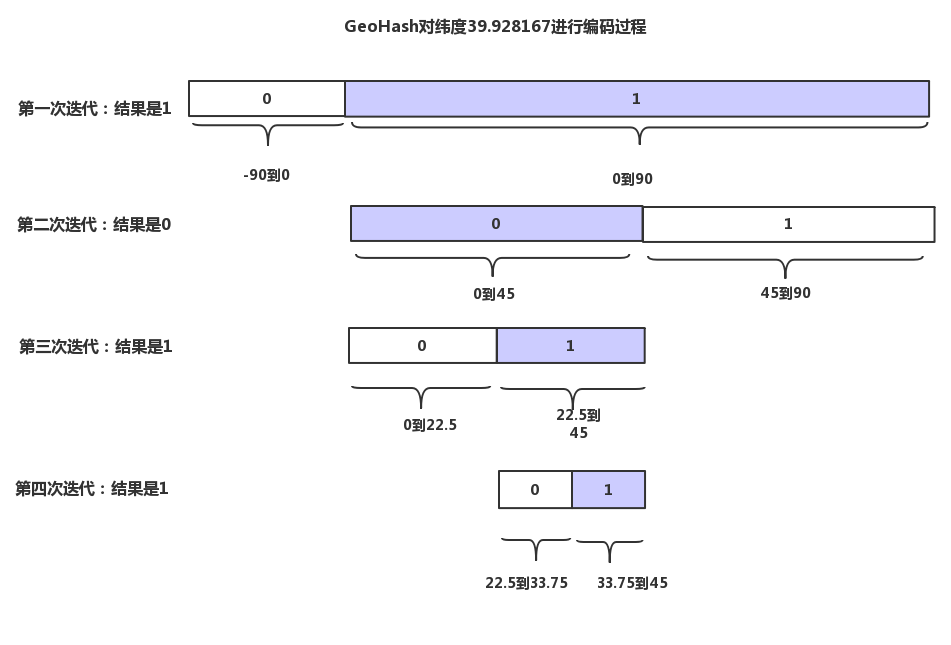
1. 第一次迭代：处于-90到0的标记为0,0到90的标记为1，39.928167处于1的区间，所以最终结果的第一位是1。
2. 第二次迭代：对上一步标记为1的部分平分，0到45标记为0,45到90标记为1，39.928167标记为1处于0的区间，所以最终结果的第二位是0。
3. 第三次迭代：对上一步标记为0的部分平分，0到22.5标记为0,22.5到45标记为1，39.928167标记为1处于0的区间，所以最终结果的第三位是0
4. 第四次迭代：对上一步标记为0的部分平分，22.5到33.75标记为0,33.75到45标记为1，39.928167标记为1处于1的区间，所以最终结果的第三位是1。

经过N次迭代后，得到一个长度为N的二进制值，比如得到的值为1011100011，这个就是对纬度进行的编码最终值。

（2）第二步：经度编码

对经度的编码过程跟对纬度编码过程十分类似，不同点是经度范围是-180到180，对经度116.389550经过N次迭代后得到编码值。比如得到1101001011。这个就是对经度编码的最终值。

（3）第三步：合并经纬度

对纬度编码值、经度编码值进行合并，合并规则是奇数位放纬度、偶数位放经度，合并为一个新的二进制串。

（4）第四步：转换为字符串

将上一步合并的二进制11100 11101 00100 01111每5位一段转换为十进制，结果是28、29、4、15，Base32编码后为wx4g。这个就是北海公园的经纬度(39.928167,116.389550)最终的GeoHash编码值。

以下图表是二进制数字、base32字符对应表：

Decimal	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Base	32	0	1	2	3	4	5	6	7	8	9	b	c	d	e	f
Decimal	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
Base	32	h	j	k	m	n	p	q	r	s	t	u	v	w	x	y