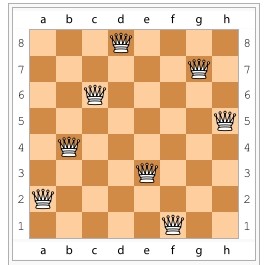
八皇后问题是一个以国际象棋为背景的问题:如何能够在 8×8 的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的n皇后摆放问题:这时棋盘的大小变为n×n,而皇后个数也变成n。当且仅当 n = 1 或 n≥ 4 时问题有解
八皇后问题最早是由国际西洋棋棋手马克斯·贝瑟尔于1848年提出。之后陆续有数学家对其进行研究,其中包括高斯和康托,并且将其推广为更一般的n皇后摆放问题。八皇后问题的第一个解是在1850年由弗朗兹·诺克给出的。诺克也是首先将问题推广到更一般的n皇后摆放问题的人之一。1874年,S.冈德尔提出了一个通过行列式来求解的方法,这个方法后来又被J.W.L.格莱舍加以改进。
艾兹格·迪杰斯特拉在1972年用这个问题为例来说明他所谓结构性编程的能力[2]。
八皇后问题在1990年代初期的著名电子游戏第七访客和NDS平台的著名电子游戏雷顿教授与不可思议的小镇中都有出现。
程序实现:
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define DIAGONAL 1
#define UNDIAGONAL 0
#define FOUND 1
#define NOTFOUND 0
#define BOARDSIZE 8
#define QUEEN 1
int check_diagonal(const int* check);
int check_duplicated(const int* check);
int clear_board(int check[BOARDSIZE][BOARDSIZE]);
int main()
{
int location[BOARDSIZE] = {0};
int board[BOARDSIZE][BOARDSIZE] = {{0}};
int row = 0;
int column = 0;
int counter = 0;
for(location[0] = 0;location[0] < BOARDSIZE;(location[0])++)
{
for(location[1] = 0;location[1] < BOARDSIZE;(location[1])++)
{
for(location[2] = 0;location[2] < BOARDSIZE;(location[2])++)
{
for(location[3] = 0;location[3] < BOARDSIZE;(location[3])++)
{
for(location[4] = 0;location[4] < BOARDSIZE;(location[4])++)
{
for(location[5] = 0;location[5] < BOARDSIZE;(location[5])++)
{
for(location[6] = 0;location[6] < BOARDSIZE;(location[6])++)
{
for(location[7] = 0;location[7] < BOARDSIZE;(location[7])++)
{
if(check_diagonal(location) == UNDIAGONAL && check_duplicated(location) == NOTFOUND)
{
clear_board(board);
counter++;
for(column = 0;column<BOARDSIZE;column++)
{
board[(location[column])][column] = QUEEN;
}
printf("Solution %d:\n",counter);
for(row = 0;row < BOARDSIZE ; row++)
{
for(column = 0;column <BOARDSIZE ; column++)
{
printf("%d ",board[row][column]);
}
printf("\n");
}
printf("\n");
}
else
{
continue;
}
}
}
}
}
}
}
}
}
return 0;
}
int check_diagonal(const int* check)
{
int former_element = 0;
int latter_element = 0;
for(former_element = 0;former_element<BOARDSIZE;former_element++)
{
for(latter_element = former_element+1;latter_element<BOARDSIZE;latter_element++)
{
if(abs(check[former_element] - check[latter_element]) == abs(former_element-latter_element))
{
return DIAGONAL;
}
}
}
return UNDIAGONAL;
}
int check_duplicated(const int* check)
{
int temp = 0;
int number = 0;
int former_element = 0;
int latter_element = 0;
for(temp = 0;temp<BOARDSIZE;temp++)
{
former_element = check[temp];
for(number = temp+1;number<BOARDSIZE;number++)
{
latter_element = check[number];
if(former_element == latter_element)
{
return FOUND;
}
}
}
return NOTFOUND;
}
int clear_board (int check[BOARDSIZE][BOARDSIZE])
{
int row = 0;
int column = 0;
for(row = 0;row <BOARDSIZE; row++)
{
for(column = 0;column< BOARDSIZE;column++)
{
check[row][column] = 0;
}
}
return 0;
}
























 2374
2374

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








