水题...
DZY loves chessboard, and he enjoys playing with it.
He has a chessboard of n rows and m columns. Some cells of the chessboard are bad, others are good. For every good cell, DZY wants to put a chessman on it. Each chessman is either white or black. After putting all chessmen, DZY wants that no two chessmen with the same color are on two adjacent cells. Two cells are adjacent if and only if they share a common edge.
You task is to find any suitable placement of chessmen on the given chessboard.
The first line contains two space-separated integers n and m (1 ≤ n, m ≤ 100).
Each of the next n lines contains a string of m characters: the j-th character of the i-th string is either "." or "-". A "." means that the corresponding cell (in the i-th row and the j-th column) is good, while a "-" means it is bad.
Output must contain n lines, each line must contain a string of m characters. The j-th character of the i-th string should be either "W", "B" or "-". Character "W" means the chessman on the cell is white, "B" means it is black, "-" means the cell is a bad cell.
If multiple answers exist, print any of them. It is guaranteed that at least one answer exists.
1 1 .
B
2 2 .. ..
BW WB
3 3 .-. --- --.
B-B --- --B
In the first sample, DZY puts a single black chessman. Of course putting a white one is also OK.
In the second sample, all 4 cells are good. No two same chessmen share an edge in the sample output.
In the third sample, no good cells are adjacent. So you can just put 3 chessmen, no matter what their colors are.
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner in=new Scanner(System.in);
int n=in.nextInt(),m=in.nextInt();
char[][] mp=new char[n+10][m+10];
for(int i=0;i<n;i++)
mp[i]=in.next().toCharArray();
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
if(mp[i][j]=='.')
{
if((i+j)%2==0)
mp[i][j]='B';
else mp[i][j]='W';
}
}
System.out.println(mp[i]);
}
}
}dfs
import java.util.*;
public class Main
{
static int[][] reactor=new int[100][100];
static boolean[] vis=new boolean[100];
static int n,m;
static long ans;
static void dfs(int u)
{
vis[u]=true;
for(int i=1;i<=n;i++)
{
if(vis[i]==true||reactor[u][i]==0) continue;
ans=ans*2;
dfs(i);
}
}
public static void main(String[] args)
{
Scanner in=new Scanner(System.in);
n=in.nextInt();m=in.nextInt();
ans=1;
while(m-->0)
{
int a=in.nextInt(),b=in.nextInt();
reactor[a][b]=reactor[b][a]=1;
}
for(int i=1;i<=n;i++)
{
if(!vis[i]) dfs(i);
}
System.out.println(ans);
}
}坑爹贪心....
别人的证明:
here's the proof.
say we have an edge of weight  connecting nodes with values
connecting nodes with values  and
and  and another edge of weight
and another edge of weight  connecting nodes with values
connecting nodes with values  and
and  .
.
- let us assume that
 and also
and also  (i.e. taking both edges together will lead to better density than taking either single edge).
(i.e. taking both edges together will lead to better density than taking either single edge). - cross multiplying the two gives
 and
and  .
. - adding
 to both sides of first equation gives
to both sides of first equation gives  .
. - combining second and third equations, we get
 , which means that
, which means that  .
.
this is a contradiction because problem statement says that all node values and edge weights are positive. so our assumption was wrong, i.e. single edge is always the right answer.
import java.util.*;
import java.math.*;
public class Main
{
public static void main(String[] args)
{
Scanner in=new Scanner(System.in);
int n=in.nextInt(),m=in.nextInt();
double ans=0.;
double[] v=new double[n+10];
for(int i=1;i<=n;i++)
{
v[i]=in.nextDouble();
}
for(int i=0;i<m;i++)
{
int a=in.nextInt(),b=in.nextInt();
double c=in.nextDouble();
ans=Math.max(ans,(v[a]+v[b])/c);
}
System.out.print(ans);
}
}
A,B都是随机生成的,c[i]=max(....)有很大概率是靠近n的,设一个界限s,逐个枚举n-s~n之间的数并检查可能性,如果找不到那就暴力计算.
DZY loves Fast Fourier Transformation, and he enjoys using it.
Fast Fourier Transformation is an algorithm used to calculate convolution. Specifically, if a, b and c are sequences with length n, which are indexed from 0 to n - 1, and
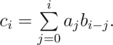
We can calculate c fast using Fast Fourier Transformation.
DZY made a little change on this formula. Now
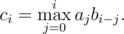
To make things easier, a is a permutation of integers from 1 to n, and b is a sequence only containing 0 and 1. Given a and b, DZY needs your help to calculate c.
Because he is naughty, DZY provides a special way to get a and b. What you need is only three integers n, d, x. After getting them, use the code below to generate a and b.
//x is 64-bit variable;
function getNextX() {
x = (x * 37 + 10007) % 1000000007;
return x;
}
function initAB() {
for(i = 0; i < n; i = i + 1){
a[i] = i + 1;
}
for(i = 0; i < n; i = i + 1){
swap(a[i], a[getNextX() % (i + 1)]);
}
for(i = 0; i < n; i = i + 1){
if (i < d)
b[i] = 1;
else
b[i] = 0;
}
for(i = 0; i < n; i = i + 1){
swap(b[i], b[getNextX() % (i + 1)]);
}
}
Operation x % y denotes remainder after division x by y. Function swap(x, y) swaps two values x and y.
The only line of input contains three space-separated integers n, d, x (1 ≤ d ≤ n ≤ 100000; 0 ≤ x ≤ 1000000006). Because DZY is naughty, x can't be equal to 27777500.
Output n lines, the i-th line should contain an integer ci - 1.
3 1 1
1 3 2
5 4 2
2 2 4 5 5
5 4 3
5 5 5 5 4
In the first sample, a is [1 3 2], b is [1 0 0], so c0 = max(1·1) = 1, c1 = max(1·0, 3·1) = 3, c2 = max(1·0, 3·0, 2·1) = 2.
In the second sample, a is [2 1 4 5 3], b is [1 1 1 0 1].
In the third sample, a is [5 2 1 4 3], b is [1 1 1 1 0].
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=1100000;
typedef long long int LL;
int a[maxn],b[maxn],q[maxn],to[maxn];
int n,d;
LL x;
int getNextX()
{
x = (x * 37 + 10007) % 1000000007;
return x;
}
void initAB()
{
int i;
for(i = 0; i < n; i = i + 1)
{
a[i] = i + 1;
}
for(i = 0; i < n; i = i + 1)
{
swap(a[i], a[getNextX() % (i + 1)]);
}
for(i = 0; i < n; i = i + 1)
{
if (i < d)
b[i] = 1;
else
b[i] = 0;
}
for(i = 0; i < n; i = i + 1)
{
swap(b[i], b[getNextX() % (i + 1)]);
}
}
int main()
{
scanf("%d%d%I64d",&n,&d,&x);
initAB();
for(int i=0;i<n;i++)
if(b[i]) q[++q[0]]=i;
for(int i=0;i<n;i++)
to[a[i]]=i;
int s=30;
for(int i=0;i<n;i++)
{
int j,flag=0;
for(j=n;j>=n-s;j--)
{
if(j>0&&to[j]<=i&&b[i-to[j]])
{
printf("%d\n",j);
flag=1;
break;
}
}
if(flag) continue;
int ans=0;
for(j=1;j<=q[0]&&q[j]<=i;j++)
{
ans=max(ans,a[i-q[j]]);
}
printf("%d\n",ans);
}
return 0;
}线段树延迟更新....
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
using namespace std;
typedef long long int LL;
const int maxn=210000;
LL color[maxn<<2],add[maxn<<2],sum[maxn<<2];
void pushup(int rt)
{
color[rt]=(color[rt<<1]==color[rt<<1|1])?color[rt<<1]:0;
sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
void pushdown(int rt,int m)
{
if(add[rt])
{
add[rt<<1]+=add[rt];
add[rt<<1|1]+=add[rt];
sum[rt<<1]+=add[rt]*(m-(m>>1));
sum[rt<<1|1]+=add[rt]*(m>>1);
add[rt]=0;
color[rt<<1]=color[rt<<1|1]=color[rt];
color[rt]=0;
}
}
void build(int l,int r,int rt)
{
if(l==r)
{
color[rt]=l;
return ;
}
int m=(l+r)/2;
build(lson); build(rson);
pushup(rt);
}
void update(int L,int R,int x,int l,int r,int rt)
{
if(L<=l&&r<=R&&color[rt])
{
sum[rt]+=abs(x-color[rt])*(r-l+1);
add[rt]+=abs(x-color[rt]);
color[rt]=x;
return ;
}
pushdown(rt,r-l+1);
int m=(l+r)/2;
if(m>=L)
update(L,R,x,lson);
if(m<R)
update(L,R,x,rson);
pushup(rt);
}
LL query(int L,int R,int l,int r,int rt)
{
if(L<=l&&r<=R)
{
return sum[rt];
}
pushdown(rt,r-l+1);
int m=(l+r)/2;
LL ret=0;
if(m>=L)
ret+=query(L,R,lson);
if(m<R)
ret+=query(L,R,rson);
return ret;
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
build(1,n,1);
while(m--)
{
int a,b,c,d;
scanf("%d",&a);
if(a==1)
{
scanf("%d%d%d",&b,&c,&d);
update(b,c,d,1,n,1);
}
else if(a==2)
{
scanf("%d%d",&c,&d);
printf("%I64d\n",query(c,d,1,n,1));
}
}
return 0;
}







 .
.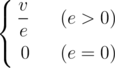
 ;
; if and only if
if and only if  , and edge
, and edge  ;
;
 . Integer
. Integer 















 732
732

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








