题目原文:
A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Now suppose you are given the locations and height of all the buildings as shown on a cityscape photo (Figure A), write a program to output the skyline formed by these buildings collectively (Figure B).
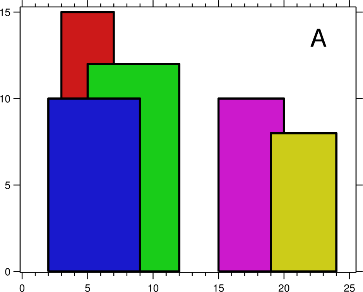
Buildings
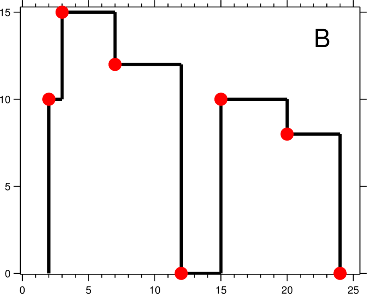
Skyline Contour
The geometric information of each building is represented by a triplet of integers [Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height. It is guaranteed that 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX, and Ri - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.
For instance, the dimensions of all buildings in Figure A are recorded as: [ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] .
The output is a list of “key points” (red dots in Figure B) in the format of [ [x1,y1], [x2, y2], [x3, y3], … ] that uniquely defines a skyline. A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour.
For instance, the skyline in Figure B should be represented as:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].
Notes:
The number of buildings in any input list is guaranteed to be in the range [0, 10000].
The input list is already sorted in ascending order by the left x position Li.
The output list must be sorted by the x position.
There must be no consecutive horizontal lines of equal height in the output skyline. For instance, […[2 3], [4 5], [7 5], [11 5], [12 7]…] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: […[2 3], [4 5], [12 7], …]
题目大意:
题干很长,就不直接翻译了。
大致是:有一些楼房,在平面直角坐标系上用矩形表示(其中y=0代表地面),按横坐标从小到大顺序求出这些大楼重叠起来的轮廓线的关键点(即可以描绘出轮廓的节点,在图B中用红点表示)。
例如,图A中的输入为:
2 9 10
3 7 15
5 12 12
15 20 10
19 24 8
输出(对应图B)为:
2 10
3 15
7 12
12 0
15 10
20 8
24 0
题目分析:
看着题目好长,而且暴力求解每一个x值对应的y值显然会超时,于是在discuss中找了一段神代码,是基于线段树的,大概意思是,先把区间离散化,然后在线段树中记录每个区间的最大高度,再遍历一遍线段树得到每个点的高度height[],,再把每个高度变化的点记录到最后返回的数组。
源码:(language:cpp)
#define left(i) (i<<1)
#define right(i) ((i<<1) + 1)
struct Node {
int nodel, noder, nodeh;
};
struct Segment {
int begin, end;
};
class Solution {
public:
vector<pair<int, int>> getSkyline(vector<vector<int>>& buildings) {
if(buildings.size() == 0) return {};
int sz = buildings.size();
vector<int> nums;
for (int i = 0; i<sz; i++) {
nums.push_back(buildings[i][0]);
nums.push_back(buildings[i][1]);
}
sort(nums.begin(), nums.end());
int pre = 0;
int numssz = nums.size();
map<int, int> m;
for (int i = 0; i < numssz; i++) {
if (pre < nums[i]) segments.push_back({ pre, nums[i] - 1 });
segments.push_back({ nums[i], nums[i] });
int idx = segments.size()-1;
m[nums[i]] = idx;
pre = nums[i]+1;
}
int segmentsnum = segments.size();
tree = vector<Node>(segmentsnum << 2, { 0, 0, 0 });
heights = vector<int>(segmentsnum+1, 0);
buildTree(1, 0, segmentsnum);
for (int i = 0; i<sz; i++) {
set(1, m[buildings[i][0]], m[buildings[i][1]]-1, buildings[i][2]);
}
getHeights();
vector<pair<int, int>> ret;
for (int i = 0; i < segmentsnum; i++) {
if (i == 0 && heights[i] != 0 || i != 0 && heights[i] != heights[i - 1]) ret.push_back(make_pair(segments[i].begin, heights[i]));
}
if (heights[segmentsnum - 1] != 0) ret.push_back(make_pair(segments[segmentsnum - 1].begin, 0));
return ret;
}
private:
vector<Node> tree;
vector<int> heights;
vector<Segment> segments;
void buildTree(int idx, int l, int r) {
tree[idx].nodel = l;
tree[idx].noder = r;
tree[idx].nodeh = 0;
if (l == r)
{
return;
}
int mid = (l + r) / 2;
buildTree(left(idx), l, mid);
buildTree(right(idx), mid + 1, r);
}
void update(int idx) {
if (tree[idx].nodel == tree[idx].noder) return;
if (tree[left(idx)].nodeh < tree[idx].nodeh) {
tree[left(idx)].nodeh = tree[idx].nodeh;
}
if (tree[right(idx)].nodeh < tree[idx].nodeh) {
tree[right(idx)].nodeh = tree[idx].nodeh;
}
tree[idx].nodeh = 0;
}
void set(int idx, int l, int r, int h) {
if (tree[idx].nodel >= l && tree[idx].noder <= r) {
tree[idx].nodeh = max(tree[idx].nodeh, h);
return;
}
int mid = (tree[idx].nodel + tree[idx].noder) / 2;
update(idx);
if (mid >= l) {
set(left(idx), l, r, h);
}
if (mid<r) {
set(right(idx), l, r, h);
}
}
void getHeights() {
queue<int> q;
q.push(1);
while (!q.empty()) {
int idx = q.front();
q.pop();
update(idx);
if (tree[idx].nodel == tree[idx].noder)
{
heights[tree[idx].nodel] = tree[idx].nodeh;
continue;
}
q.push(left(idx));
q.push(right(idx));
}
}
};成绩:
112ms,100%,836ms,10.74%
cmershen的碎碎念:
线段树在是acm中比较常见的数据结构,常用于区间查询和更改,但leetcode中涉及的不多。这道题的题解里面大多是用优先队列来做。






















 1146
1146

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








