排序算法总结（Java泛型实现）

游戏规则

我们关注的主要对象是重新排列数组元素的算法，其中每个元素都有一个主键，排序算法的目标就是将所有元素的主键按照某种方式排列。在Java中，元素通常都是对象，对主键的抽象描述是通过一种内置的机制（Comparable接口）来完成的。
大多数情况下，我们的排序代码只会通过两个方法操作数据：less()方法对元素进行比较，exch方法将元素交换位置。将数据操作限制在这两个方法中使得代码的可读性和可移植性更好，更容易验证代码的正确性、分析性能以及排序算法之间的比较。
我们的排序算法模板适用于任何实现了Comparable接口的数据类型。例如，Java中封装数字的类型Integer和Double，以及String和其他许多高级数据类型（如File和URL）都实现了Comparable，因此可以直接使用这些类型的数组作为参数调用我们的排序方法。
在创建自己的数据类型时，只需要实现Comparable接口就能够保证用例代码可以将其排序。要做到这一点，只需要实现一个compareTo()方法来定义目标类型对象的自然次序即可。

自定义数据类型实现Comparable接口

下面是一个自定义类型HolidayDate，使用日期作为主键进行比较：

public class HolidayDate implements Comparable<HolidayDate>
{
    private final String name;
    private final int day;
    private final int month;
    public HolidayDate(String n, int m, int d) {
        name = n;
        day = d;
        month = m;
    }
    public int day() {
        return day;
    }
    public int month() {
        return month;
    }
    public String name() {
        return name;
    }
    public int compareTo(HolidayDate that) {
        if(this.month > that.month) return 1;
        if(this.month < that.month) return -1;
        if(this.day > that.day) return 1;
        if(this.day < that.day) return -1;
        return 0;
    }
    public String toString() {
        return name + " is in " + month + "/" + day;
    }
}

数据操作的泛型方法less()和exch()

protected static boolean less(Comparable v, Comparable w) {
        return v.compareTo(w) < 0;
    }

protected static void exch(Comparable[] a, int i, int j) {
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }

打印数组的泛型方法show

protected static void show(Comparable[] a) {
        // 打印数组
        for(int i = 0; i < a.length; i++) {
            System.out.println(a[i]);
        }
    }

选择排序

算法原理：
首先找到数组中最小的那个元素，其次，将它和数组的第一个元素交换位置。再次，在剩下的元素中找到最小的元素，将它与数组的第二个元素交换位置。如此往复，直到将整个数组排序。
算法特点：
运行时间和输入无关，取决于比较的次数；
数据移动是最少的，使用了N次交换。
算法实现：

public static void sort(Comparable[] a) {
        // 将a[]按升序排列
        int N = a.length;
        for(int i = 0; i < N; i++) {
            // 将a[i]和a[i+1...N]中最小的元素交换
            int min = i;
            for(int j = i+1 ; j < N; j++) {
                if(less(a[j], a[min])) {
                    min = j;
                }
            }
            exch(a, i, min);
        }
    }

插入排序

算法原理：
像排序一手扑克牌，一张一张的进行整理，将每一张牌插入到其他已经有序的牌中的适当位置。实现时，为了给要插入的元素腾出空间，我们需要将其余所有元素在插入之前都向右移动一位。
算法特点：
运行时间取决于输入中元素的初始顺序。如对一个其中的元素已经（接近）有序的数组进行排序将会比对随机顺序的数组或逆序数组进行排序要快得多。
算法实现：

public static void sort(Comparable[] a) {
        // 将a[]按升序排列
        int N = a.length;
        for(int i = 1; i < N; i++) {
            // 将 a[i]插入到a[i-1]、a[i-2]、...之中
            for(int j = i; j > 0 && less(a[j], a[j-1]); j--) {
                exch(a, j, j-1);
            }
        }
    }

希尔排序

算法原理：
希尔排序为了加快速度简单地改进了插入排序，交换不相邻的元素以对数组的局部进行排序，并最终用插入排序对局部有序的数组排序。希尔排序的思想是使数组中任意间隔为h的元素都是有序的。在进行排序时，如果h很大，我们就能将元素移动到很远的地方，为实现更小的h有序创造方便。用这种方式，对于任意以1结尾的h序列，我们都能够将数组排序。
算法特点：
权衡了子数组的规模和有序性。排序之初，各个子数组都很短，排序之后的子数组都是部分有序的。这两种情况都很适合插入排序。
目前还没有人给出选取最好的增量因子序列的方法。
算法实现：

public static void sort(Comparable[] a) {
        // 将a[]按升序排列
        int N = a.length;
        int h = 1;
        while(h < N/3) {
            h = 3*h + 1;
        }
        while(h >= 1) {
            // 将数组变为h有序
            for(int i = h; i < N; i++) {
                // 将 a[i]插入到a[i-h], a[i-2*h], ...之中
                for(int j = i; j >= h && less(a[j], a[j-h]); j -= h) {
                    exch(a, j, j-h);
                }
            }
            h = h/3;
        }
    }

归并排序

算法原理：
先递归地将数组分成两半分别排序，然后将结果归并起来。
算法特点：
运行时间与NlogN成正比，适用于处理数百万甚至更大规模的数组；
缺点是所需的额外空间与N成正比；
算法实现：

private static Comparable[] aux;
private static void sort(Comparable[] a) {
        aux = new Comparable[a.length]; // 一次性分配空间
        sort(a, 0, a.length-1);
    }
public static void sort(Comparable[] a, int lo, int hi) {
        // 将数组a[lo..hi]自顶向下地归并排序
        if(hi <= lo)
            return;
        int mid = lo + (hi - lo)/2;
        sort(a, lo, mid);   // 将左半边排序
        sort(a, mid+1, hi);     // 将右半边排序
        merge(a, lo, mid, hi);  // 归并结果
    }
private static void merge(Comparable[] a, int lo, int mid, int hi) {
        // 将a[lo..mid]和a[mid+1..hi]原地归并
        int i = lo, j = mid+1;
        // 将a[lo..hi]复制到aux[lo..hi]
        for(int k = lo; k <= hi; k++)
            aux[k] = a[k];
        // 归并回到a[lo..hi]
        for(int k = lo; k <= hi; k++)
            if(i > mid) // 左半边用尽，取右半边的元素
                a[k] = aux[j++];
            else if(j > hi) // 右半边用尽，取左半边的元素
                a[k] = aux[i++];
            else if(less(aux[j], aux[i]))   // 右半边的当前元素小于左半边的当前元素，取右半边的元素
                a[k] = aux[j++];
            else    // 右半边的当前元素大于等于左半边的当前元素，取左半边的元素
                a[k] = aux[i++];
    }

public static void sort(Comparable[] a) {
        // 将数组a自底向上地归并排序
        int N = a.length;
        aux = new Comparable[N];
        for(int sz = 1; sz < N; sz = sz+sz) // sz子数组大小
            for(int lo = 0; lo < N-sz; lo += sz+sz) // lo:子数组索引
                merge(a, lo, lo+sz-1, Math.min(lo+sz+sz-1, N-1));
    }

算法改进：
对小规模子数组使用插入排序；
测试数组是否已经有序，如果a[mid]小于等于a[mid+1]，则跳过merge()方法；
不将元素复制到辅助数组，在递归调用的每个层次交换输入数组和辅助数组的角色，节省将数组元素复制到用于归并的辅助数组所用的时间。

快速排序

算法原理：
将一个数组分成两个数组，将两部分独立地排序，当这两个子数组都有序时整个数组也就自然有序了。快速排序和归并排序是互补的，在归并排序中一个数组被等分为两半，在快速排序中切分的位置取决于数组的内容。
快速排序的关键在于切分，这个过程使得数组满足三个条件：

1. 对于某个j，a[j]已经排定；
2. a[lo]到a[j-1]中的所有元素都不大于a[j]；
3. a[j+1]到a[hi]中的所有元素都不小于a[j]；

算法特点：
原地排序，只需要一个很小的辅助栈；
运行时间和NlgN成正比；
非常脆弱，在实现时需要非常小心才能避免低劣的性能（平方级别）。
算法实现：

public static void sort(Comparable[] a) {
        sort(a, 0, a.length-1);
    }
    private static void sort(Comparable[] a, int lo, int hi) {
        if(hi <= lo)
            return ;
        int j = partition(a, lo, hi);   // 切分
        sort(a, lo, j-1);   // 将左半部分排序
        sort(a, j+1, hi);   // 将右半部分排序
    }
    private static int partition(Comparable[] a, int lo, int hi) {
        // 将数组切分为a[lo..i-1], a[i], a[i+1..hi]
        int i = lo, j = hi+1;   // 左右扫描指针
        Comparable v = a[lo];   // 切分元素
        while(true) {
            // 扫描左右， 检查扫描是否结束并交换元素
            while(less(a[++i], v))
                if(i == hi)
                    break;
            while(less(v, a[--j]))
                if(j == lo)
                    break;
            if(i >= j)
                break;
            exch(a, i, j);  
        }
        exch(a, lo, j); // 将v = a[j]放入正确 的位置
        return j;   // a[lo..j-1] <= a[j] <= a[j+1..hi]达成
    }

堆排序

算法原理：
堆排序可以分为两个阶段。在堆的构造阶段，将原始数组重新组织并安排进一个堆中；然后在下沉排序阶段，从堆中按递减顺序取出所有元素并得到排序结果。
算法特点：
在排序时将需要排序的数组本身作为堆，无需任何额外空间；
运行时间为NlogN；
算法实现：

public static void sort(Comparable[] a) {
        int N = a.length-1; // 数组a存储在a[0..N]上
        for (int k = N/2; k >= 0; k--)  // 最大堆的构造阶段
            sink(a, k, N);
        while(N > 0) {  // 下沉排序阶段
            exch(a, 0, N--);    // 将最大元素从a[0]交换至a[N]
            sink(a, 0, N);  // N-1后，重新下沉调整有序堆a[0..N]
        }
    }
private static void exch(Comparable[] a, int i, int j) {
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
    private static void sink(Comparable[] a, int k, int N) {
        // 由上至下的堆有序化（下沉）
        while (2*k <= N) {
            int j = 2*k;
            if(j < N && less(a, j, j+1))
                j++;
            if(!less(a, k, j))
                break;
            exch(a, k, j);
            k = j;
        }
    }
private static boolean less(Comparable[] a, int i, int j) {
        return a[i].compareTo(a[j]) < 0;
    }

冒泡排序

算法原理：
在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的数往上冒。
算法实现：

public static void sort(Comparable[] a) {
        boolean exchange;   // 交换标志
        for(int i = 0; i < a.length; i++) {
            exchange = false;   // 本趟排序开始前，交换标志设为假 
            for(int j = a.length-1; j > i; j--) {
                if(less(a[j], a[j-1])) {
                    exch(a, j, j-1);
                    exchange = true; // 发生了交换，故将交换标志置为真
                }
            }
            if(!exchange)   //本趟没有发生交换，提前终止算法  
                return;
        }
    }

使用样例

public static void main(String args[]) {
        HolidayDate newyears = new HolidayDate("newyears", 1, 1);
        HolidayDate valentine = new HolidayDate("valentine", 2, 14);
        HolidayDate christmas = new HolidayDate("christmas", 12, 25);
        HolidayDate birthday = new HolidayDate("birthday", 9, 3);
        HolidayDate dragonboat = new HolidayDate("dragonboat", 5, 5);
        HolidayDate teacher = new HolidayDate("dragonboat", 9, 10);
        HolidayDate midautumn = new HolidayDate("midautumn", 8, 15);
        HolidayDate[] holiday = {christmas, birthday, teacher, newyears, midautumn,
                valentine, dragonboat};
        sort(holiday);
        show(holiday);
    }

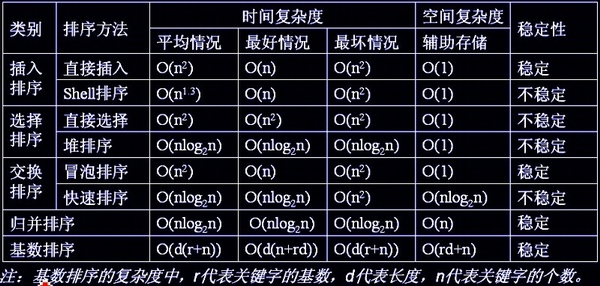
性能比较

参考资料

《Algorithms -Fourth Edition》Robert Sedgewick&&Kevin Wayne著