[Leetcode] 28, 8, 5

28. Implement strStr()

Implement strStr().

Returns the index of the first occurrence of needle in haystack, or -1 if needle is not part of haystack.

Solution(1): 直接暴力求解，时间复杂度O(m*n)，面试时这样做就可以了。

Code:

class Solution {
public:
    int strStr(string haystack, string needle) {
        if(needle.size()==0) return 0;
        if(haystack.size() < needle.size()) return -1;
        for(int i=0; i<=haystack.size()-needle.size(); i++){
            int t;
            for(t=0; t<needle.size(); t++){
                if(needle[t] != haystack[i+t]) break;
            }
            if(t==needle.size()) return i;
        }
        return -1;
    }
};

Solution(2): 使用KMP算法快速求解，时间复杂度O(m+n)。

注意：如果使用vector<int> next(s.size(),0); 在函数返回时会报错

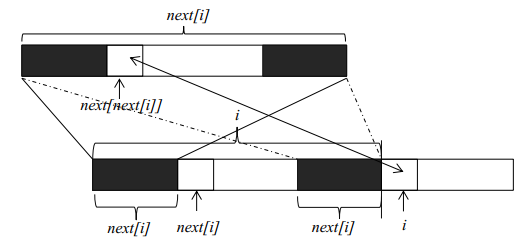
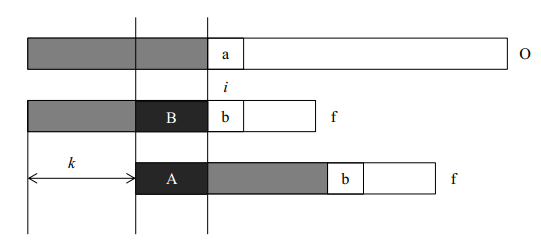
首先求出needle对应的next数组：

然后在求subString的时候，遇到相异点时，可以通过next数组快速找到子序列中可以复用的部分：

详细解释参考博客：

http://www.cnblogs.com/c-cloud/p/3224788.html

http://blog.csdn.net/yutianzuijin/article/details/11954939/

Code:

class Solution {
public:
    int strStr(string haystack, string needle) {
        if(haystack.size()<needle.size()) return -1;
        else if(needle.size()==0) return 0;
        else if(needle.size()==1){
            for(int i=0; i<haystack.size(); i++){
                if(haystack[i]==needle[0]) return i;
            }
            return -1;
        }
        
        
        vector<int> next;
        for(int i=0; i<needle.size(); i++)
            next.push_back(0);
        compute_next(needle,next);
        int ih = 0; //haystack下标
        int in = 0; //needle下标
        while(ih<haystack.size() && in<needle.size()){
            if(haystack[ih]==needle[in]){
                ih++;
                in++;
                
                if(in==needle.size()){
                    return ih-in;
                }
            }else if(in!=0){
                //in=3时，表示前面已有3个字符相等，因此找3个字符组成的子序列中的前后缀最长重合部分个数next[3]
                //此时haystack起点处为ih-in
                in = next[in];
            }else{
                ih++;
            }
        }
        cout<<"end"<<endl;
        return -1;
    }
private:
    static void compute_next(string needle, vector<int>& next){
        // needle.size > 1
        //（动规）用于计算KMP算法中的next数组
        // next[i]表示needle前i位构成的子数组的最长相等前缀后缀的长度
        // needle = abcdefabc... -> next[8] = 3
        next[0] = 0;
        next[1] = 0;
        for(int i=1; i<needle.size(); i++){
            //next[i]->needle[i-1]，注意两个数组下标是错开的
            if(needle[i]==needle[next[i]]){
                next[i+1] = next[i]+1;
            }else{
                next[i+1] = 0;
                int index = next[i];
                do{
                    index = next[index];
                    if(needle[i]==needle[index]){
                        next[i+1] = index+1;
                        break;
                    }
                }while(index>0);
            }
        }
    }
};

8. String to Integer (atoi)

Implement atoi to convert a string to an integer.

Hint: Carefully consider all possible input cases. If you want a challenge, please do not see below and ask yourself what are the possible input cases.

Notes: It is intended for this problem to be specified vaguely (ie, no given input specs). You are responsible to gather all the input requirements up front.

Update (2015-02-10):
The signature of the C++ function had been updated. If you still see your function signature accepts a const char * argument, please click the reload button  to reset your code definition.

Solution: 此题不难，只要注意处理几种特殊情况即可。

Code:

class Solution {
public:
    int myAtoi(string str) {
        int ans = 0;
        if(str.size()==0) return 0;
        
        int i=0;
        
        //注意空格，空格在最前面时合法
        for(;i<str.size(); i++)
            if(str[i]!=' ') break;
        
        //注意正负号，正负号直接接着数字合法
        int sign = 1;
        if(str[i]=='+') i++;
        else if(str[i]=='-'){
            sign = -1;
            i++;
        }
        
        
        for(; i<str.size(); i++){
            if(str[i]>'9' || str[i]<'0') break; //遇到非数字停止
            if(ans > INT_MAX/10 || 
               (ans == INT_MAX/10 && str[i]-'0' > INT_MAX % 10)) //注意数字越界，越界就不再累积
                return sign==-1 ? INT_MIN:INT_MAX;
            ans = ans*10 + (str[i]-'0');
                
        }
        return sign * ans;
    }
};

5. Longest Palindromic Substring

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example:

Input: "babad"

Output: "bab"

Note: "aba" is also a valid answer.

Example:

Input: "cbbd"

Output: "bb"

Solution(1): 直接暴力求解即可，O(n^3)。

Code:

class Solution {
public:
    string longestPalindrome(string s) {
        string pstring = "";
        for(int i=0; i<s.size(); i++){
            string newstring = "";
            newstring.push_back(s[i]);
            for(int t=s.size()-1; t>i; t--){
                int begin = i;
                int end = t;
                while(begin<end){
                    if(s[begin]!=s[end]) break;
                    begin++;
                    end--;
                }
                if(begin>=end){
                    newstring = s.substr(i,t-i+1);
                    break;
                }
            }
            if(newstring.size()>pstring.size())
                pstring = newstring;
        }
        return pstring;
    }
};

Solution(2): 暴力求解2，从中间向两边找，即可O(n^2)。

Code:

class Solution {
public:
    string longestPalindrome(string s) {
        string pstring = "";
        for(int i=0; i<s.size(); i++){
            //以i作为中间的单独数
            int t0 = i-1;
            int t1 = i+1;
            int count = 1;
            calsubPalin(t0,t1,count,s);
            if(count>pstring.size()) pstring = s.substr(t0,t1-t0+1);
            //以i和i-1或i和i+1作为中间的数
            count = 0;
            t0 = i-1;
            t1 = i;
            calsubPalin(t0,t1,count,s);
            if(count>pstring.size()) pstring = s.substr(t0,t1-t0+1);
            count = 0;
            t0 = i;
            t1 = i+1;
            calsubPalin(t0,t1,count,s);
            if(count>pstring.size()) pstring = s.substr(t0,t1-t0+1);
        }
        return pstring;
    }
private:
    static void calsubPalin(int& t0, int& t1, int& count, string& s){
        
        while(t0>=0 && t1<s.size()){
            if(s[t0]==s[t1]){
                count+=2;
                t0--;
                t1++;
            }
            else break;
        }
        t0++;
        t1--;
    }
};

Solution(3): 经典算法Manacher’s Algorithm，时间复杂度O(n)。

详细解释参考：http://blog.csdn.net/hopeztm/article/details/7932245

注意：这篇博客有个地方是错的。if P[ i' ] ≤ R – i 改成 if P[ i' ] ＜ R – i ，否则会出错，因为当半径正好到边界的时候，也要进一步试探真实长度。

Code:

class Solution {
public:
    string longestPalindrome(string s) {
        string dummys = "$";//避免试探R范围时需要检查边界
        //插入'#'，避免分类讨论
        for(int i=0; i<s.size(); i++){
            dummys.push_back('#');
            dummys.push_back(s[i]);
        }
        dummys.push_back('#');
        
        vector<int> P;
        P.push_back(0);
        P.push_back(0);
        int C = 1; 
        int maxC = 1;
        for(int i=2; dummys[i]; i++){
            if(i < C+P[C]){
                int t = 2*C-i;
                if(P[t]<C+P[C]-i) P.push_back(P[t]);
                else{
                    int R = C+P[C]-i;
                    //试探R的范围
                    while(dummys[i-R] == dummys[i+R]) R++;
                    R--;
                    P.push_back(R);
                }
                if(P[i]+i>P[C]+C) C = i;
                if(P[i]>P[maxC]) maxC = i;
            }else{
                int R = 1;
                //试探R的范围
                while(dummys[i-R] == dummys[i+R]) R++;
                R--;
                P.push_back(R);
                if(P[i]+i>P[C]+C) C = i;
                if(P[i]>P[maxC]) maxC = i;
            }
        }
        
        string ans = "";
        for(int i=maxC-P[maxC]; i<=maxC+P[maxC]; i++){
            if(dummys[i]!='#') ans.push_back(dummys[i]);
        }
        return ans;
    }
};