【数论】莫比乌斯反演(欧拉反演)进阶-杜教筛

前言

这里需要对莫反有一些基础。
不会的可以点这里

回忆

• $f(n)={\sum }_{d|n}g(d)\to g(n)={\sum }_{d|n}f(d)\mu (\frac{n}{d})$
• ${\sum }_{d|n}\mu (d)=[n=1]$
• ${\sum }_{i=1}^n\lfloor \frac{n}{i}\rfloor =$ 你应该知道怎么求
• ${\sum }_{i=1}^{10^9}\mu (i)=$ 你可能需要知道怎么求
• 线性筛 $\mu (i),\phi (i)$
• 一些数学能力

题集

1

${\prod }_{i=1}^n{\prod }_{j=1}^m\gcd (i,j)$
$={\prod }_{d=1}{d}^{{\sum }_{i=1}{\sum }_{j=1}^m[\gcd (i,j)=d]}$
$={\prod }_{d=1}{d}^{{\sum }_{k=1}^{\frac{\min (n,m)}{d}}\mu (k)\frac{n}{kd}\frac{m}{kd}}$
$={\prod }_{T=1}({\prod }_{k|T}(\frac{T}{k}{)}^{\mu (k)}{)}^{\frac{n}{T}\frac{m}{T}}$
令 $f(T)={\prod }_{k|T}(\frac{T}{k}{)}^{\mu (k)}$
线性筛+整出分块即可
Code:

#include<bits/stdc++.h>
#define int long long
#define IOS ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
#define cou(i) cout<<fixed<<setprecision(i)
using namespace std;
const int N=1e7+1,mod=1e9+7;
int t,n,m,k,ans,res;
unordered_map<int,int>Mu;
struct fy{
	int prv[N],cnt,mu[N],F[N];
	bool pr[N];
	int qmi(int x,int y){
		int res=1;
		while(y>0){
			if(y&1)
				res=res*x%mod;
			x=x*x%mod,y>>=1;
		}
		return res;
	}
	void ola(int x){
		pr[1]=mu[1]=F[1]=1;
		for(int i=2;i<=x;i++){
			if(!pr[i])
				prv[++cnt]=i,mu[i]=-1,F[i]=i;
			for(int j=1;j<=cnt&&i*prv[j]<=x;j++){
				int u=i*prv[j];
				pr[u]=1;
				if(i%prv[j]==0){
					mu[u]=0;
					F[u]=F[i];
					break;
				}
				else{
					mu[u]=-mu[i];
					F[u]=1;
				}
			}
		}
	}
	void getsum(int x){
		F[0]=1;
		for(int i=1;i<=x;i++){
			F[i]*=F[i-1],F[i]%=mod; 
		}
	}
	int summu(int x){
		int res=1;
		if(x<N)
			return mu[x];
		if(Mu[x])
			return Mu[x];
		for(int l=2,r;l<=x;l=r+1){
			r=x/(x/l);
			res-=(summu(x/l))*(r-l+1);
		}
		Mu[x]=res;
		return res;
	}
	int sumphi(int x){
		int res=0;
		for(int l=1,r;l<=x;l=r+1){
			r=x/(x/l);
			res+=(summu(r)-summu(l-1))*(x/l)*(x/l);
		}
		return res;
	}
}A;
signed main(){
	IOS;
	A.ola(N-1);
	A.getsum(N-1);
	cin>>t;
	while(t--){
		cin>>n>>m;
		int ans=1ll;
		for(int l=1,r;l<=min(n,m);l=r+1){
			r=min(n/(n/l),m/(m/l));
			int res=A.F[r]*A.qmi(A.F[l-1],mod-2)%mod;
			ans=ans*A.qmi(res,(n/l)*(m/l))%mod;
		}
		cout<<ans<<"\n";
	}
	return 0;
}

经验：
1
2
3

2

Link

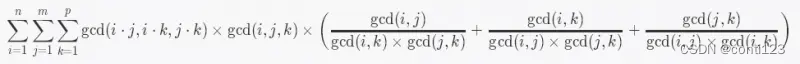
暴力推式子。
关键:
$\gcd (ij,jk,ki)=\frac{\gcd (i,j)\gcd (j,k)\gcd (k,i)}{\gcd (i,j,k)}$
然后可得原式=于神之怒加强版或这里
好像这黑题有那么一点点水啊
Code:

#include<bits/stdc++.h>
#define int long long
#define IOS ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
using namespace std;
const int N=2e7+1,mod=1e9+7;
int t,n,m,p,k;
struct fy{
	int prv[N],cnt,g[N],s[N];
	bool pr[N];
	inline int qmi(int x,int y){
		int res=1;
		while(y>0){
			if(y&1)
				res=res*x%mod;
			x=x*x%mod,y>>=1;
		}
		return res;
	}
	void ola(int x){
		pr[1]=g[1]=1;
		for(int i=2;i<=x;i++){
			if(!pr[i])
				prv[++cnt]=i,g[i]=(qmi(i,k)-1+mod)%mod;
			for(int j=1;j<=cnt&&i*prv[j]<=x;j++){
				int u=i*prv[j];
				pr[u]=1;
				if(i%prv[j]==0){
					g[u]=g[i]*qmi(prv[j],k)%mod;
					break;
				}
				else{
					g[u]=g[i]*g[prv[j]]%mod;
				}
			}
		}
	}
	void getsum(int x){
		for(int i=1;i<=x;i++)
			g[i]=(g[i]+g[i-1])%mod;
	}
}A;
signed main(){
	IOS;
	k=2;
	cin>>t;
	A.ola(N-1);
	A.getsum(N-1);
	while(t--){
		cin>>n>>m>>p;
		int ans=0,res=0;
		for(int l=1,r;l<=min(n,m);l=r+1){
			r=min(n/(n/l),m/(m/l));
			res+=(n/l)*(m/l)%mod*((A.g[r]-A.g[l-1]+mod)%mod)%mod;
			res%=mod;
		}
		ans+=res*p;
		ans%=mod;
		res=0;
		for(int l=1,r;l<=min(m,p);l=r+1){
			r=min(m/(m/l),p/(p/l));
			res+=(m/l)*(p/l)%mod*((A.g[r]-A.g[l-1]+mod)%mod)%mod;
			res%=mod;
		}
		ans+=res*n;
		ans%=mod;
		res=0;
		for(int l=1,r;l<=min(p,n);l=r+1){
			r=min(p/(p/l),n/(n/l));
			res+=(p/l)*(n/l)%mod*((A.g[r]-A.g[l-1]+mod)%mod)%mod;
			res%=mod;
		}
		ans+=res*m;
		ans%=mod;
		cout<<ans<<"\n";
	}
	return 0;
}

杜教筛

来自 OI-wiki的资料：

这里直达

这里直达OI-wiki

---

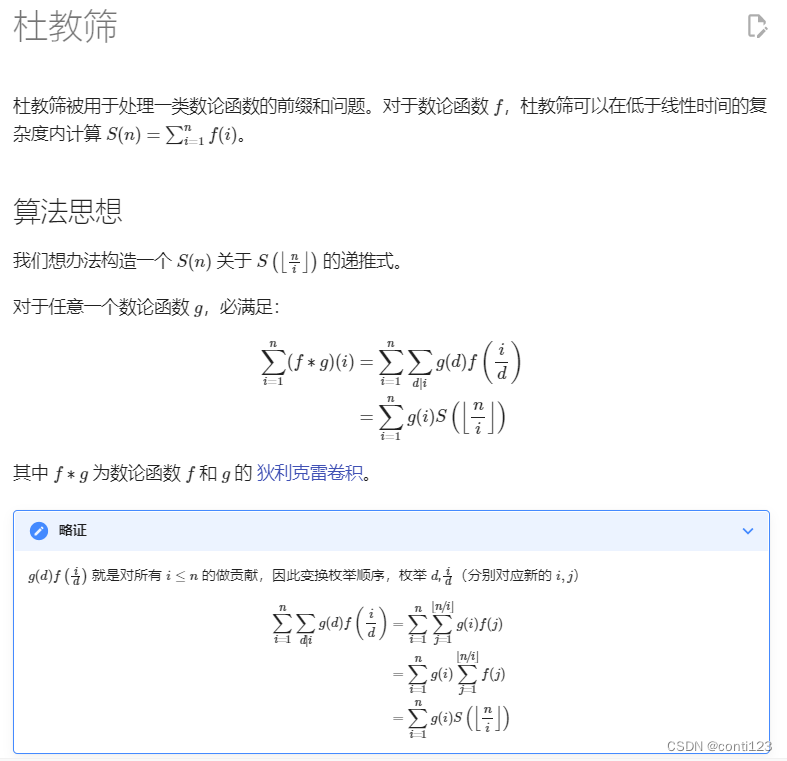
例题

给定一个正整数，求
$an{s}_1={\sum }_{i=1}^n\phi (i),an{s}_2={\sum }_{i=1}^n\mu (i)$
输入的第一行为一个整数，表示数据组数 $T$。
接下来 $T$ 行，每行一个整数 $n$，表示一组询问。
对于每组询问，输出一行两个整数，分别代表 $an{s}_1$ 和 $an{s}_2$。
对于全部的测试点，保证 $1\le T\le 10$，$1\le n<2^{31}$。
考虑使用杜教筛。
设 $S_1(n)={\sum }_{i=1}^n\mu (i)$


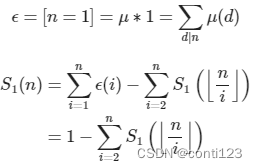
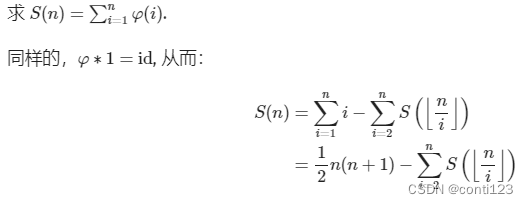
那样我们就完成了两个最简单的例题了
Code:

#include<bits/stdc++.h>
#define int __int128
using namespace std;
const int N=2e6+1,mod=1e9+7;
int t,n,m,k;
void write(int x){
	if(x<0)
		putchar('-'),x=-x;
	if(x>=10)
		write((int)(x/10));
	char o='0'+x%10;
	putchar(o);
}
void read(int &x){
	x=0;
	int y=1;
	char c=getchar();
	while(c>'9'||c<'0'){
		if(c=='-'){
			y=-1;
			break;
		}
		c=getchar();
	}
	while(c<='9'&&c>='0')
		x=x*10+c-'0',c=getchar();
	x*=y;
}
map<int,int>Mu,Phi;
struct fy{
	int prv[N],cnt,phi[N],mu[N];
	bool pr[N];
	void ola(int x){
		pr[1]=mu[1]=1;
		for(int i=2;i<=x;i++){
			if(!pr[i])
				prv[++cnt]=i,mu[i]=-1;
			for(int j=1;j<=cnt&&i*prv[j]<=x;j++){
				int u=i*prv[j];
				pr[u]=1;
				if(i%prv[j]==0){
					mu[u]=0;
					break;
				}
				else{
					mu[u]=-mu[i];
				}
			}
		}
	}
	void getsumF(int x){
		for(int i=1;i<=x;i++)
			mu[i]+=mu[i-1];
	}
	int summu(int x){
		int res=1;
		if(x<N)
			return mu[x];
		if(Mu[x])
			return Mu[x];
		for(int l=2,r;l<=x;l=r+1){
			r=x/(x/l);
			res-=(summu(x/l))*(r-l+1);
		}
		Mu[x]=res;
		return res;
	}
	int sumphi(int x){
		int res=0;
		for(int l=1,r;l<=x;l=r+1){
			r=x/(x/l);
			res+=(summu(r)-summu(l-1))*(n/l)*(n/l);
		}
		return res;
	}
}A;
signed main(){
	A.ola(N-1);
	A.getsumF(N-1);
	read(t);
	while(t--){
		read(n);
		write((A.sumphi(n)-1)/2+1);
		putchar(' ');
		write(A.summu(n));
		putchar('\n');
	}
	return 0;
}
//此代码有一点瑕疵，但确实可以过模板题