本学期学校里学习了几种群智能优化算法,笔者闲来无事研究大乱斗出装,遂用遗传算法计算LOLM腕豪蓄意轰拳伤害最大化出装,由于装备的效果过于离散,并且技能伤害由两个因素影响:额外生命值以及攻击力,在遗传算法进行价差互换操作时,尽管可能父辈是优秀个体也可能产生子代为全肉或者全输出导致蓄意轰拳伤害不佳,所以遗传算法并不是解决出装问题的好方法,本文完全为笔者一时兴起,娱乐之举,请大家不要较真。
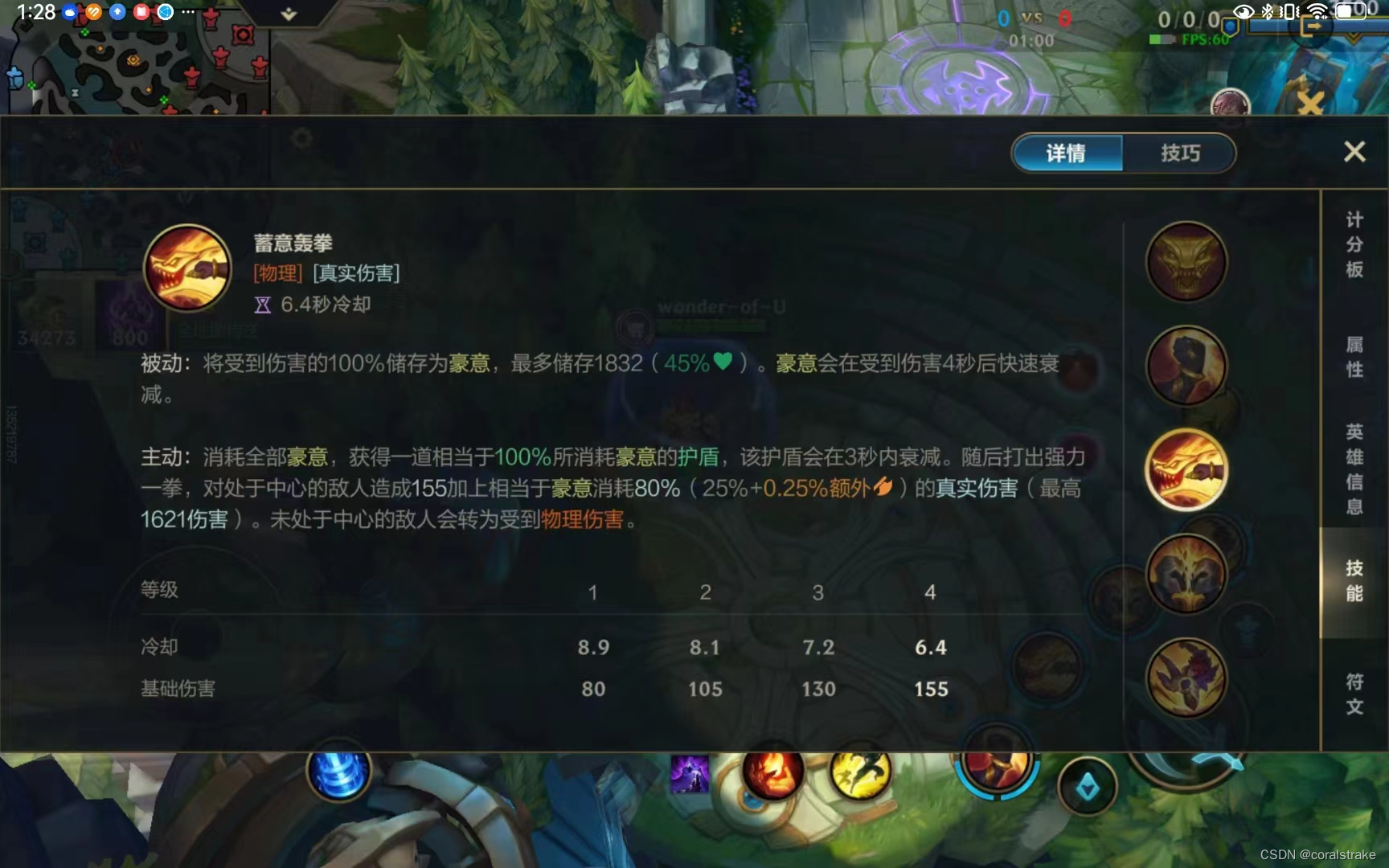
以下是对技能的一些介绍:
瑟提
15级 基础生命 2220 基础攻击力109
豪意值 最大生命上限的45%
蓄意轰拳中心 155加上豪意值*{25%+0.25*额外攻击力%}向上取整
W = 155+(2220+Σy)*0.45*(25+{Σx/4})/100
这里的W即为目标函数
下面列举能影响到蓄意轰拳的全部装备
| 装备名称 | 攻击力(x) | 血量(y) |
| 守护天使 | 40 | 0 |
| 饮血剑 | 50 | 0 |
| 分裂弓 | 20 | 0 |
| 暮刃 | 55 | 0 |
| 凡性的提醒 | 30 | 0 |
| 魔宗 | 25 | 0 |
| 黑切 | 40 | 350 |
| 三相 | 30 | 250 |
| 饮魔刀 | 55 | 0 |
| 死亡之舞 | 35 | 0 |
| 幻影之舞 | 25 | 0 |
| 吸蓝刀(特殊被动) | 40 | 0 |
| 岚切 | 40 | 0 |
| 赛瑞尔达 | 40 | 0 |
| 迅刃 | 45 | 0 |
| 夜之锋刃 | 50 | 250 |
| 神分 | 25 | 425 |
| 巨蛇之牙 | 50 | 0 |
| 盾攻 | 40 | 0 |
| 收集者 | 40 | 0 |
| 炼金锯 | 45 | 250 |
| 青龙刀 | 50 | 300 |
| 幽梦 | 55 | 0 |
| 破败王者之刃 | 20 | 0 |
| 无尽 | 55 | -5(5-50) |
| 界弓 | 40 | 0 |
| 巨九 | 0 | 550 |
| 血手 | 0 | 400 |
| 日炎 | 0 | 500 |
| 振奋铠甲 | 0 | 350 |
| 兰盾 | 0 | 400 |
| 反甲 | 0 | 200 |
| 亡者的板甲 | 0 | 250 |
| 冰拳 | 0 | 250 |
| 深渊面具 | 0 | 300 |
| 基克的聚合 | 0 | 300 |
| 守护之誓 | 0 | 350 |
| 冬之降临 | 0 | 350 |
| 自然之力 | 0 | 350 |
| 种子罐 | 0 | 425 |
| 午时斗篷 | 0 | 200 |
| 炽光之冠 | 0 | 300 |
| 心之钢 | 0 | 700 |
| 狂徒 | 0 | 700 |
| 炽阳法袍 | 0 | 250 |
6件装备除去鞋子只有5件装备可以选择
筛选
只加攻击排名前五的装备
| 暮刃 | 55 | 0 |
| 饮魔刀 | 55 | 0 |
| 幽梦 | 55 | 0 |
| 饮血剑 | 50 | 0 |
| 巨蛇之牙 | 50 | 0 |
只加血量排名前五的装备
| 心之钢 | 0 | 700 |
| 狂徒 | 0 | 700 |
| 巨九 | 0(特殊被动) | 550 |
| 日炎 | 0 | 500 |
| 种子罐 | 0 | 425 |
既加攻击又加血量装备
| 黑切 | 40 | 350 |
| 三相 | 30 | 250 |
| 夜之锋刃 | 50 | 250 |
| 神分 | 25 | 425 |
| 炼金锯 | 45 | 250 |
| 青龙刀 | 50 | 300 |
攻击加的很多但是减少血量的装备
| 无尽 | 55 | -5(5-50) |
经上述筛选,装备选择范围缩小至以下范围
| 装备名称 | 攻击力 | 血量 |
| 暮刃 | 55 | 0 |
| 饮魔刀 | 55 | 0 |
| 幽梦 | 55 | 0 |
| 饮血剑 | 50 | 0 |
| 巨蛇之牙 | 50 | 0 |
| 心之钢 | 0 | 700 |
| 狂徒 | 0 | 700 |
| 巨九 | 0 | 550 |
| 日炎 | 0 | 500 |
| 种子罐 | 0 | 425 |
| 黑切 | 40 | 350 |
| 三相 | 30 | 250 |
| 夜之锋刃 | 50 | 250 |
| 神分 | 25 | 425 |
| 炼金锯 | 45 | 250 |
| 青龙刀 | 50 | 300 |
| 无尽 | 55 | -5(5-50) |
鞋子(只计算加伤害和加血量最高的装备)
| 贪婪之靴 | 35 | 0 |
| 水银之靴 | 0 | 200 |
特殊装备
心之刚:层数转化为最大生命(1层1滴血)
巨型九头蛇(巨像):获得15+2.5%额外生命值的攻击力
将代码按照有无巨型九头蛇分为两个代码分别求最优,并且分别可以又用户输入心之刚层数
代码1 无巨九
import math
import random
import copy
import numpy as np
def DP(population, equip, shoes):
pope = population[0]
pops = population[1]
totaly = sum(equip[i][1] for i in pope) + shoes[pops][1]
totalx = sum(equip[i][0] for i in pope) + shoes[pops][0]
w = 155 + (2220 + totaly) * 0.45 * (25 + math.ceil(totalx / 4)) / 100
return w
def creat_population():
pope = random.sample(range(16), 5)
pops = random.randint(0, 1)
return [pope, pops]
def creat_populations(popsize):
populations = []
for i in range(popsize):
populations.append(creat_population())
return populations
def fitness(populations, popsize, equip, shoes):
fitness = []
for i in range(popsize):
fitness.append(DP(populations[i], equip, shoes))
return fitness
def PMX(p, q):
a = p[0]
b = q[0]
a1 = copy.deepcopy(a)
b1 = copy.deepcopy(b)
x = random.randint(0, len(a1))
y = random.randint(0, len(a1))
while x >= y:
x = random.randint(0, len(a1))
y = random.randint(0, len(a1))
af = a1[x:y]
bf = b1[x:y]
a1_1 = []
a1_2 = []
b1_1 = []
b1_2 = []
for i in a1[:x]:
while i in bf:
i = af[bf.index(i)]
a1_1.append(i)
for i in a1[y:]:
while i in bf:
i = af[bf.index(i)]
a1_2.append(i)
for i in b1[:x]:
while i in af:
i = bf[af.index(i)]
b1_1.append(i)
for i in b1[y:]:
while i in af:
i = bf[af.index(i)]
b1_2.append(i)
child1 = a1_1 + bf + a1_2
child2 = b1_1 + af + b1_2
return [child1, p[1]], [child2, q[1]]
def roulette_wheel_selection(fitness):
s = sum(fitness)
normalized_fitness = [f / s for f in fitness]
selection_probs = np.cumsum(normalized_fitness)
rand_selection = np.random.rand()
for i, prob in enumerate(selection_probs):
if rand_selection < prob:
return i
def find_fittest(fitness, popsize):
key = 0
fittest = 0
for i in range(popsize):
if fitness[i] > key:
key = fitness[i]
fittest = i
return fittest
def trans(lst):
sorted_indices = sorted(range(len(lst)), key=lambda k: lst[k])
return [sorted_indices.index(i) for i in range(len(lst))]
def mutate(ind, populations):
idx1, idx2 = random.sample(range(len(populations[ind][0])), 2)
populations[ind][0][idx1] = random.randint(0, 15)
populations[ind][0][idx2] = random.randint(0, 15)
populations[ind][0] = trans(populations[ind][0])
return populations
def find_fittest_individual(populations, fitness_values, popsize):
fittest_index = find_fittest(fitness_values, popsize)
return populations[fittest_index]
def main():
popsize = 300
n_generations = 100
mutation_prob = 0.2
mutation_increment = 0.1
best_fitness_overall = 0
best_individual_overall = None
best_generation = 0
gang = 1500
equip = [[55, 0], [55, 0], [55, 0], [50, 0], [50, 0], [0, 700+int(gang)], [0, 700], [0, 500], [0, 425],
[40, 350], [30, 250], [50, 250], [25, 425], [45, 250], [50, 300], [55, -5]]
shoes = [[35, 0], [0, 200]]
equip_name = ["暮刃", "饮魔刀", "幽梦", "饮血剑", "巨蛇之牙", "心之钢", "狂徒", "日炎", "种子罐", "黑切",
"三相", "夜之锋刃", "神分", "炼金锯", "青龙刀", "无尽"]
shoes_name = ["贪婪之靴", "水银之靴"]
populations = creat_populations(popsize)
fitness_values = fitness(populations, popsize, equip, shoes)
best_fitness_per_generation = []
for generation in range(n_generations):
new_populations = []
for i in range(0, popsize, 2):
parent1_index = roulette_wheel_selection(fitness_values)
parent2_index = roulette_wheel_selection(fitness_values)
while True:
if parent1_index == parent2_index:
parent2_index = roulette_wheel_selection(fitness_values)
else:
break
parent1 = populations[parent1_index]
parent2 = populations[parent2_index]
child1, child2 = PMX(parent1, parent2)
new_populations.append(child1)
new_populations.append(child2)
for i in range(popsize):
if random.random() < mutation_prob:
populations = mutate(i, populations)
fitness_values = fitness(new_populations, popsize, equip, shoes)
mutation_prob += mutation_increment
fittest_individual = find_fittest_individual(new_populations, fitness_values, popsize)
fittest_fitness = max(fitness_values)
if fittest_fitness > best_fitness_overall:
best_fitness_overall = fittest_fitness
best_individual_overall = fittest_individual
best_generation = generation
best_fitness_per_generation.append((generation, fittest_fitness))
# 输出每一代的最佳适应度和解决方案
print(f"第 {generation} 代: 最佳适应度: {fittest_fitness}")
print("装备方案:", [equip_name[i] for i in fittest_individual[0]])
print("鞋子:", shoes_name[fittest_individual[1]])
# 输出全局最佳解
print("\n全局最佳解:")
print(f"第 {best_generation} 代: 最佳适应度: {best_fitness_overall}")
print("装备方案:", [equip_name[i] for i in best_individual_overall[0]])
print("鞋子:", shoes_name[best_individual_overall[1]])
print(f"最高伤害:{math.ceil(best_fitness_overall)}")
print(f"此时心之刚层数为:{gang}")
return best_fitness_per_generation
if __name__ == "__main__":
main()
代码2 有巨九
import math
import random
import copy
import numpy as np
def DP(population, equip, shoes):
pope = population[0]
pops = population[1]
totaly = sum(equip[i][1] for i in pope) + shoes[pops][1]
totalx = sum(equip[i][0] for i in pope) + shoes[pops][0]
w = 155 + (2220 + totaly) * 0.45 * (25 + math.ceil(totalx / 4)) / 100
return w
def creat_population():
pope = random.sample(range(16), 4)
pops = random.randint(0, 1)
return [pope, pops]
def creat_populations(popsize):
populations = []
for i in range(popsize):
populations.append(creat_population())
return populations
def fitness(populations, popsize, equip, shoes):
fitness = []
for i in range(popsize):
fitness.append(DP(populations[i], equip, shoes))
return fitness
def PMX(p, q):
a = p[0]
b = q[0]
a1 = copy.deepcopy(a)
b1 = copy.deepcopy(b)
x = random.randint(0, len(a1))
y = random.randint(0, len(a1))
while x >= y:
x = random.randint(0, len(a1))
y = random.randint(0, len(a1))
af = a1[x:y]
bf = b1[x:y]
a1_1 = []
a1_2 = []
b1_1 = []
b1_2 = []
for i in a1[:x]:
while i in bf:
i = af[bf.index(i)]
a1_1.append(i)
for i in a1[y:]:
while i in bf:
i = af[bf.index(i)]
a1_2.append(i)
for i in b1[:x]:
while i in af:
i = bf[af.index(i)]
b1_1.append(i)
for i in b1[y:]:
while i in af:
i = bf[af.index(i)]
b1_2.append(i)
child1 = a1_1 + bf + a1_2
child2 = b1_1 + af + b1_2
return [child1, p[1]], [child2, q[1]]
def roulette_wheel_selection(fitness):
s = sum(fitness)
normalized_fitness = [f / s for f in fitness]
selection_probs = np.cumsum(normalized_fitness)
rand_selection = np.random.rand()
for i, prob in enumerate(selection_probs):
if rand_selection < prob:
return i
def find_fittest(fitness, popsize):
key = 0
fittest = 0
for i in range(popsize):
if fitness[i] > key:
key = fitness[i]
fittest = i
return fittest
def trans(lst):
sorted_indices = sorted(range(len(lst)), key=lambda k: lst[k])
return [sorted_indices.index(i) for i in range(len(lst))]
def mutate(ind, populations):
idx1, idx2 = random.sample(range(len(populations[ind][0])), 2)
populations[ind][0][idx1] = random.randint(0, 15)
populations[ind][0][idx2] = random.randint(0, 15)
populations[ind][0] = trans(populations[ind][0])
return populations
def find_fittest_individual(populations, fitness_values, popsize):
fittest_index = find_fittest(fitness_values, popsize)
return populations[fittest_index]
def DP_1(population, equip, shoes):
pope = population[0]
pops = population[1]
totaly = 0
totalx = 0
for i in pope:
totaly += equip[i][1]
totalx += equip[i][0]
totaly += shoes[pops][1]
totalx += shoes[pops][0]
totaly += 550
totalx += 15+2.5*totaly/100
w = 155+(2220+totaly)*0.45*(25+math.ceil(totalx/4))/100
return w
def main():
popsize = 200
n_generations = 100
mutation_prob = 0.2
mutation_increment = 0.1
best_fitness_overall = 0
best_individual_overall = None
best_generation = 0
gang = 1500
equip = [[55, 0], [55, 0], [55, 0], [50, 0], [50, 0], [0, 700+int(gang)], [0, 700], [0, 500], [0, 425],
[40, 350], [30, 250], [50, 250], [25, 425], [45, 250], [50, 300], [55, -5]]
shoes = [[35, 0], [0, 200]]
equip_name = ["暮刃", "饮魔刀", "幽梦", "饮血剑", "巨蛇之牙", "心之钢", "狂徒", "日炎", "种子罐", "黑切",
"三相", "夜之锋刃", "神分", "炼金锯", "青龙刀", "无尽"]
shoes_name = ["贪婪之靴", "水银之靴"]
populations = creat_populations(popsize)
fitness_values = fitness(populations, popsize, equip, shoes)
best_fitness_per_generation = []
for generation in range(n_generations):
new_populations = []
for i in range(0, popsize, 2):
parent1_index = roulette_wheel_selection(fitness_values)
parent2_index = roulette_wheel_selection(fitness_values)
while True:
if parent1_index == parent2_index:
parent2_index = roulette_wheel_selection(fitness_values)
else:
break
parent1 = populations[parent1_index]
parent2 = populations[parent2_index]
child1, child2 = PMX(parent1, parent2)
new_populations.append(child1)
new_populations.append(child2)
for i in range(popsize):
if random.random() < mutation_prob:
populations = mutate(i, populations)
fitness_values = fitness(new_populations, popsize, equip, shoes)
mutation_prob += mutation_increment
fittest_individual = find_fittest_individual(new_populations, fitness_values, popsize)
fittest_fitness = max(fitness_values)
if fittest_fitness > best_fitness_overall:
best_fitness_overall = fittest_fitness
best_individual_overall = fittest_individual
best_generation = generation
best_fitness_per_generation.append((generation, fittest_fitness))
# 输出每一代的最佳适应度和解决方案
print(f"第 {generation} 代: 最佳适应度: {fittest_fitness}")
print("装备方案:", [equip_name[i] for i in fittest_individual[0]])
print("鞋子:", shoes_name[fittest_individual[1]])
# 输出全局最佳解
print("\n全局最佳解:")
print(f"第 {best_generation} 代: 最佳适应度: {best_fitness_overall}")
print("装备方案:巨型九头蛇", [equip_name[i] for i in best_individual_overall[0]])
print("鞋子:", shoes_name[best_individual_overall[1]])
print(f"最高伤害:{math.ceil(DP_1([[i for i in best_individual_overall[0]], best_individual_overall[1]],equip, shoes))}")
print(f"此时心之刚层数为:{gang}")
return best_fitness_per_generation
if __name__ == "__main__":
main()
上述两个代码心之刚层数都定为1500层,跑出来较优的解如图:


由于心之刚层数不好控制,笔者也计算了心之刚层数为0且不出巨型九头蛇时的数据为例,进入游戏进行考证

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








