简介
图(Graph)是一种较线性表和树更为复杂的数据结构。在线性表中,数据元素之间仅有线性关系,即每个数据元素只有一个直接前驱和一个直接后继;在树形结构中,数据元素之间有着明显的层次关系,虽然每一层上的数据元素可能和下一层中多个元素(孩子) 相关,但只能和上一层中一个元素(双亲)相关;而在图形结构中,结点之间的关系可以是任意的,任意两个数据元素之间都可能相关。
图在各个领域都有着广泛的应用,如电路网络分析、交通运输、管理与线路的铺设、印刷电路板与集成电路的布线等众多直接与图有关的问题,它们必须用图的有关方法进行处理;另外像工作的分配、工程进度的安排、课程表的制订、关系数据库的设计等许多实际问题,如果间接地用图来表示,处理起来比较方便。这些技术领域都是把图作为解决问题的主要数学手段来使用,因此,如何在计算机中表示和处理图结构,就是计算机科学需研究的一项重要课题。
本章主要讨论图的逻辑表示、在计算机中的存储方法及一些有关图的算法和应用。以求解决一些实际问题。有关图论的内容可参考离散数学的内容。
学习重点
1、理解图的基本概念,熟悉图的各种存储结构及其构造算法;
2、熟练掌握图的两种搜索路径的遍历;
3、掌握构造最小生成树的方法,并理解算法;
4、理解用Dijkstra方法求解单源最短路径问题;
5、掌握求活动网络的拓扑排序的方法,并理解算法;
6、掌握求解关键路径的方法。
图的二元组定义
图G由两个集合V和E组成,记为:
G=(V,E)
其中:
V是顶点的有穷非空集合,
E是V中顶点偶对(称为边)的有穷集。
通常,也将图G的顶点集和边集分别记为V(G)和E(G)。E(G)可以是空集。若E(G)为空,则图G只有顶点而没有边。
有向图和无向图
1.有向图
若图G中的每条边都是有方向的,则称G为有向图(Digraph)。
(1)有向边的表示
在有向图中,一条有向边是由两个顶点组成的有序对,有序对通常用尖括号表示。有向边也称为弧(Arc),边的始点称为弧尾(Tail),终点称为弧头(Head)。
【例】<vi,vj>表示一条有向边,vi是边的始点(起点),vj是边的终点。因此,<vi,vj>和<vj,vi>是两条不同的有向边。
(2)有向图的表示
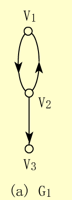
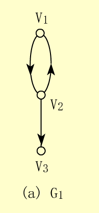
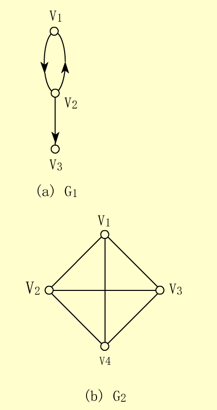
【例】下面(a)图中G1是一个有向图。图中边的方向是用从始点指向终点的箭头表示的,该图的顶点集和边集分别为:
V(G1)={v1,v2,v3}
E(G1)={<v1,v2>,<v2,v1>,<v2,v3>}
2.无向图
若图G中的每条边都是没有方向的,则称G为无向图(Undigraph)。
(1)无向边的表示
无向图中的边均是顶点的无序对,无序对通常用圆括号表示。
【例】无序对(vi,vj)和(vj,vi)表示同一条边。
(2)无向图的表示
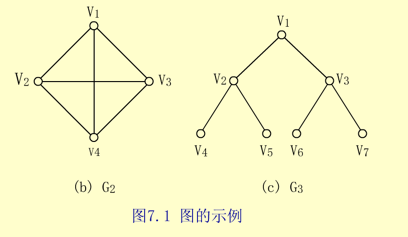
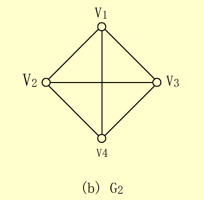
【例】下面(b)图中的G2和(c)图中的G3均是无向图,它们的顶点集和边集分别为:
V(G2)={v1,v2,v3,v4}
E(G2)={(vl,v2),(v1,v3),(v1,v4),(v2,v3),(v2,v4),(v3,v4)}
V(G3)={v1,v2,v3,v4,v5,v6,v7}
E(G3)={(v1,v2),(vl,v3),(v2,v4),(v2,v5),(v3,v6),(v3,v7)}
注意:
在以下讨论中,不考虑顶点到其自身的边。即若(v1,v2)或<vl,v2>是E(G)中的一条边,则要求v1≠v2。此外,不允许一条边在图中重复出现,即只讨论简单的图。
3.图G的顶点数n和边数e的关系
(1)若G是无向图,则0≤e≤n(n-1)/2
恰有n(n-1)/2条边的无向图称无向完全图(Undireet-ed Complete Graph)
(2)若G是有向图,则0≤e≤n(n-1)。
恰有n(n-1)条边的有向图称为有向完全图(Directed Complete Graph)。
注意:
完全图具有最多的边数。任意一对顶点间均有边相连。
【例】上面(b)图的G2就是具有4个顶点的无向完全图。
图的边和顶点的关系
1.无向边和顶点关系
若(vi,vj)是一条无向边,则称顶点vi和vj互为邻接点(Adjacent),或称vi和vj相邻接;并称(vi,vj)依附或关联(Incident)于顶点vi和vj,或称(vi,vj)与顶点vi和vj相关联。
【例】下图G2中:
① 与顶点v1相邻接的顶点是v2,v3和v4
② 关联于顶点v2的边是(v1,v2),(v2,v3)和(v2,v4)
2.有向边和顶点关系
若<vi,vj>是一条有向边,则称顶点vi邻接到vj,顶点vi邻接于顶点vj;并称边<vi,vj>关联于vi和vj或称<vi,vj>与顶点vi和vj相关联
【例】在下图G1中,关联于顶点v2的弧是<v1,v2>,<v2,v1>和<v2,v3>。
3.顶点的度(Degree)
(1)无向图中顶点v的度(Degree)
无向图中顶点v的度(Degree)是关联于该顶点的边的数目,记为D(v)。
【例】上图G2中顶点v1的度为3
(2)有向图顶点v的入度(InDegree)
有向图中,以顶点v为终点的边的数目称为v的入度(Indegree),记为ID(v)。
【例】上图G1中顶点v2的人度为l
(3)有向图顶点v的出度(Outdegree)
有向图中,以顶点v为始点的边的数目,称为v的出度(Outdegree),记为OD(v)
【例】上图G1中顶点v2的出度为2
注意:
①有向图中,顶点v的度定义为该顶点的入度和出度之和,即D(v)=ID(v)+OD(v)。
【例】上图G1中顶点v2的人度为l,出度为2,则度为3。
②无论有向图还是无向图,顶点数n、边数e和度数之间有如下关系:
子图
设G=(V,E)是一个图,若V'是V的子集,E'是E的子集,且E'中的边所关联的顶点均在V'中,则G'=(V',E')也是一个图,并称其为G的子图(Subgraph)。
【例】图7.2给出了有向图Gl的若干子图;图7.3给出了无向图G2的若干个子图。
注意:
设V'={v1,v2,v3},E'={(vl,v2),(v2,v4)},显然,V'属于V(G2),E'属于E(G2),但因为E'中序偶对(v2,v4)所关联的顶点v4不在V'中,所以(V',E')不是图,也就不可能是G2的子图。
路径(Path)
1.无向图的路径
在无向图G中,若存在一个顶点序列vp,vi1,vi2,…,vim,vq,使得(vp,vi1),(vi1,vi2),…,(vim,vq)均属于E(G),则称顶点vp到vq存在一条路径(Path)。
2.有向图的路径
在有向图G中,路径也是有向的,它由E(G)中的有向边<vp,vi1>,<vi1,vi2>,…,<vim,vq>组成。
3.路径长度
路径长度定义为该路径上边的数目。
4.简单路径
若一条路径上除了vp和vq可以相同外,其余顶点均不相同,则称此路径为一条简单路径。
【例】在图G2中顶点序列vl,v2,v3,v4是一条从顶点v1到顶点v4的长度为3的简单路径
【例】在图G2中,顶点序列v1,v2,v4,v1,v3是一条从顶点v1到顶点v3的长度为4的路径,但不是简单路径;
5.简单回路或简单环(Cycle)
起点和终点相同(vp=vq)的简单路径称为简单回路或简单环(Cycle)。
【例】图G2中,顶点序列v1,v2,v4,v1是一个长度为3的简单环
【例】有向图G1中,顶点序列v1,v2,v1是一长度为2的有向简单环。
6.有根图和图的根
在一个有向图中,若存在一个顶点v,从该顶点有路径可以到达图中其它所有顶点,则称此有向图为有根图,v称作图的根。
连通图和连通分量
1.顶点间的连通性
在无向图G中,若从顶点v i 到顶点v j 有路径(当然从v j 到v i 也一定有路径),则称v i 和v j 是连通的。
2.连通图
若V(G)中任意两个不同的顶点v i 和v j 都连通(即有路径),则称G为连通图(Con-nected Graph)。
【例】图G 2 ,和G 3 是连通图。

3.连通分量
无向图G的极大连通子图称为G的连通分量(Connected Component)。
注意:
① 任何连通图的连通分量只有一个,即是其自身
② 非连通的无向图有多个连通分量。
【例】下图中的G 4 是非连通图,它有两个连通分量H 1 和H 2 。

强连通图和强连通分量
1.强连通图
有向图G中,若对于V(G)中任意两个不同的顶点v i 和v j ,都存在从v i 到v j 以及从v j 到v i 的路径,则称G是强连通图
2.强连通分量
有向图的极大强连通子图称为G的强连通分量。
注意:
① 强连通图只有一个强连通分量,即是其自身。
② 非强连通的有向图有多个强连分量。
【例】下图中的G 1 不是强连通图,因为v 3 到v 2 没有路径,但它有两个强连通分量,如右图所示。

网络(Network)
若将图的每条边都赋上一个权,则称这种带权图为网络(Network)。
注意:
权是表示两个顶点之间的距离、耗费等具有某种意义的数。
【例】下图就是一个网络的例子。

转载自: http://sjjp.tjuci.edu.cn/sjjg/DataStructure/DS/web/gailun/gailun1.1.1b.htm








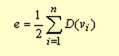














 3131
3131

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








