定义
差分约束系统(system of dierence constraints),是求解多个不等式的合法解的算法,因以两变量之差与一常量关系的形式出现,故称作差分约束。
数学形式表示如下:
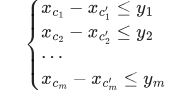
该算法旨在对于以上 n 个未知数,m 个不等式的不等式组求解。
算法
不妨将式子变换形式,即 x i x_i xi ≤ \leq ≤ x j x_j xj + + + y k y_k yk,可以发现,该式子和最短路算法中的松弛操作有异曲同工之妙,考虑将问题转化为最短路的求解。
作为今人的我们,常常说 “不难发现”,“显然” 来评价算法的核心思想,但其实,每一个算法都是学者们经过千万次演算的沉淀才诞生的结晶,我们是携着前人的基础继续探索的,所以体会不到发明算法的困难程度。也正如该算法一样,从不等式到图论的转化过程其实非常不易,难以想到。
对于最短路算法,我们曾学过 dijkstra 和 spfa 两种,虽然 dijkstra 的时间复杂度更加优异,但无法对带负权的图进行处理。
学习最短路时,我们曾得出几个结论:
- 在最短路上,一定有 d i s v dis_v disv ≤ \leq ≤ d i s u dis_u disu + + + w w w
- 最短路中一定不包含环
以下给出简易证明:
- 若 d i s v dis_v disv > > > d i s u dis_u disu + w w w,那么可将 s → \rightarrow → v 的路径更新为 s → \rightarrow → u → \rightarrow → v,与最短路定义矛盾。
- 若存在负环,则可遍历该环无穷次,不存在最短路。若存在正环,则 s → \rightarrow → v → \rightarrow → a → \rightarrow → b → \rightarrow → v 一定比 s → \rightarrow → v 更劣,与最短路定义矛盾。
有了以上两个结论,便可考虑将不等式转化为一条边 x j x_j xj → \rightarrow → x i x_i xi,权值为 w w w,根据结论 1,对该图求解最短路,则一定满足 x i x_i xi ≤ \leq ≤ x j x_j xj + + + w w w。
我们将 x i x_i xi 视作了 d i s i dis_i disi 进行求解,那么对于一组可行解, d i s i dis_i disi = = = x i x_i xi。
考虑不存在可行解的情况,根据结论 2 可知,若求解出的路径中存在负环,则不存在最短路,即意味着无可行解。
倘若题目中涉及求最大解或最小解,对于最短路来说,对于任意 i 来说 d i s i dis_i disi 都无法再次增大,否则不满足路径权值和最小,所以最短路求解的是最大值,反之最长路求解的是最小值。
实现
上述内容中,提出要建立一条 x j x_j xj → \rightarrow → x i x_i xi 权值为 w w w 的有向边,因为存在 w w w ≤ \leq ≤ 0 0 0 的情况,所以差分约束系统只能通过 spfa 进行实现。
对于图不联通的情况,不妨建立一个汇点连接每一个点,以该点为起点进行最短路求解,但是要注意此时 spfa 的判环条件会随之改变,每一条边可能会被用作松弛 n 次,而非 n - 1 次。
代码流程如下:
- 输入存边
- 建立汇点连边
- 最短路求解
- 判无解 / / / 输出
这里放置一道模板题【模板】差分约束算法
代码#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 4e5 + 5;
int n , m , vis[MAXN] , cnt , s , t , head[MAXN];
int dis[MAXN];
struct edge{
int to , nxt , w;
}e[MAXN];
void add(int u , int v , int w) { // 链式前向星存边
e[++ cnt].to = v;
e[cnt].nxt = head[u];
e[cnt].w = w;
head[u] = cnt;
}
queue<int> q;
void Spfa() { // 最短路求解
memset(dis , 0x3f , sizeof(dis));
dis[0] = 0;
q.push(0);
while(!q.empty()) {
int u = q.front();
q.pop();
for (int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].to;
if (dis[v] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
vis[v] ++;
if (vis[v] == n + 1) // spfa 判断是否存在负环
printf("No");
exit(0);
}
q.push(v);
}
}
}
}
int main() {
scanf("%d %d", &n , &m);
for (int i = 1 , u , v , w ; i <= m ; i ++) {
scanf("%d %d %d", &u , &v , &w);
add(v , u , w);
}
for (int i = 1 ; i <= n ; i ++) add(0 , i , 0); // 建立汇点
Spfa();
for (int i = 1 ; i <= n ; i ++) printf("%d ", dis[i]); // 输出可行解
return 0;
}
扩展
上述内容中,我们只考虑了 x i x_i xi − - − x j x_j xj ≤ \leq ≤ w k w_k wk 的形式,但某些题目中还可能存在如下形式:
- x i x_i xi − - − x j x_j xj < < < w k w_k wk
- x i x_i xi − - − x j x_j xj ≥ \geq ≥ w k w_k wk
- x i x_i xi − - − x j x_j xj > > > w k w_k wk
- x i x_i xi − - − x j x_j xj = = = 0 0 0
处理:
- 在 x i x_i xi 与 x j x_j xj 为整数的情况下,可转化为 x i x_i xi − - − x j x_j xj ≤ \leq ≤ w k w_k wk − - − 1 1 1
- 将两边同时乘以 -1,可转化为 x j x_j xj − - − x i x_i xi ≤ \leq ≤ − w k -w_k −wk
- 同理在 x i x_i xi 与 x j x_j xj 为整数的情况下,可转化为 x j x_j xj − - − x i x_i xi ≤ \leq ≤ − 1 -1 −1 − - − w k w_k wk
- 将等式拆成两个不等式, x i x_i xi − - − x j x_j xj ≥ \geq ≥ 0 0 0 与 x i x_i xi − - − x j x_j xj ≤ \leq ≤ 0 0 0,再进行处理即可
该题是差分约束系统的大杂烩,涵盖五种不等式。需要注意的是该题有实际意义,每一个小朋友分到的糖果数量不能为零,所以建立汇点连边时边权不再为 0,而是 1。
该题是四川省选原题,所以数据对 spfa 有着严格的要求,需要加入 SLF 优化才能勉强卡过,详情请见此处SPFA的优化
代码#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 4e5 + 5;
int n , m , vis[MAXN] , cnt , s , t , head[MAXN];
ll dis[MAXN] , ans;
char B[1 << 15], *S = B, *T = B, obuf[1 << 15], *p3 = obuf;
#define getchar() (S == T && (T = (S = B) + fread(B, 1, 1 << 15, stdin), S == T) ? EOF : *S++)
template <typename item>
void read(item &x) {
char c(getchar());
x = 0;
int f(1);
while (c > '9' || c < '0') {
if (c == '-')f = -1;
c = getchar();
}
while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
x *= f;
}
struct edge{
int to , nxt , w;
}e[MAXN];
void add(int u , int v , int w) {
e[++ cnt].to = v;
e[cnt].nxt = head[u];
e[cnt].w = w;
head[u] = cnt;
}
deque<int> q;//将普通队列进阶为双端队列
void Spfa() {
dis[0] = 0;
q.push_back(0);
while(!q.empty()) {
int u = q.front();
q.pop_front();
for (int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].to;
if (dis[v] < dis[u] + e[i].w) { // 最长路来求最小值
dis[v] = dis[u] + e[i].w;
vis[v] ++;
if (vis[v] == n) {
printf("-1");
exit(0);
}
// SLF优化
if (q.size() && dis[q.front()] <= dis[v]) q.push_front(v);
else q.push_back(v);
}
}
}
}
int main() {
read(n);
read(m);
for (int i = 1 , op , u , v ; i <= m ; i ++) {
read(op) , read(u) , read(v);
// 因为该题存在实际意义,改变存边方式,思想相同
if (op == 1) {
add(u , v , 0);
add(v , u , 0);
} else if (op == 2) {
if (u == v) {
return printf("-1") , 0;
}
add(u , v , 1);
} else if (op == 3) {
add(v , u , 0);
} else if (op == 4) {
if (u == v) {
return printf("-1") , 0;
}
add(v , u , 1);
} else {
add(u , v , 0);
}
}
for (int i = 1 ; i <= n ; i ++) add(0 , i , 1); // 注意边权为 1
Spfa();
for (int i = 1 ; i <= n ; i ++) ans += dis[i];
printf("%lld", ans);
return 0;
}
习题
组一组
简化题意如下:
构造一个含有 n 个元素的序列 a,给定 m1 个区间
[
l
i
,
r
i
]
[l_i , r_i]
[li,ri] 使得该区间按位或和为
w
w
w,给定 m2 个区间
[
l
i
,
r
i
]
[l_i , r_i]
[li,ri] 使得该区间为按位与和为
w
w
w。
初次分析这道题,由于该题涉及到了位运算,较容易想到将序列 a 转换为 2 进制的形式进行思考,那么对于题目条件限制,可得如下结论:
不妨令
w
i
w_i
wi 为
w
w
w 二进制表示形式的第 i 位,并对
w
i
w_i
wi 进行分讨。
- 若 w i = 1 w_i=1 wi=1,对于按位与操作来说,则要求 [ l i , r i ] [l_i , r_i] [li,ri] 之中任意数二进制的第 i 位都为 1,对于按位或操作来说,则要求 [ l i , r i ] [l_i , r_i] [li,ri] 之中至少一个数的二进制第 i 位为 1。
- 若 w i = 0 w_i=0 wi=0,对于按位与操作来说,则要求 [ l i , r i ] [l_i , r_i] [li,ri] 之中至少一个数的二进制第 i 位为 0,对于按位或操作来说,则要求 [ l i , r i ] [l_i , r_i] [li,ri] 之中任意数的二进制第 i 位都为 0。
由于该题是区间处理,可考虑加入前缀和解决问题。
对于二进制的第 i 位,令 p r e j pre_j prej 为前 j 个数二进制第 i 位的和,则可通过限制条件得出以下不等式:
- 若 w i = 1 w_i=1 wi=1,对于按位与操作来说,则 p r e r − p r e l − 1 = r − l + 1 pre_r - pre_{l-1} = r-l+1 prer−prel−1=r−l+1,对于按位或操作来说,则 p r e r − p r e l − 1 ≥ 1 pre_r - pre_{l-1} \geq 1 prer−prel−1≥1。
- 若 w i = 0 w_i=0 wi=0,对于按位与操作来说,则 p r e r − p r e l − 1 ≤ r − l pre_r - pre_{l-1} \leq r-l prer−prel−1≤r−l,对于按位或操作来说,则 p r e r − p r e l − 1 = 0 pre_r - pre_{l-1} = 0 prer−prel−1=0。
有了以上不等式,我们即可建立差分约束系统,求出 pre 序列,从而差分求出满足题意的 a 序列。
注意事项:
- 该题因为 0 号节点被占用,所以不能像往常一样将 0 号节点作为汇点,而是以 n + 1 节点作为汇点。
- 该题数据由我们敬爱的学长 llsw 精心制作,所以使用 spfa 的时候需加入 SLF 优化。
- 该题需要进行多次 spfa,记得初始化。
- 对于前缀和数组本身也有 p r e i ≥ p r e i − 1 pre_i \geq pre_{i-1} prei≥prei−1, p r e i − 1 ≤ p r e i {pre_{i-1} \leq pre_i} prei−1≤prei 的条件,记得连边。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e6 + 5;
int n , m , s , t , dis[MAXN] , op[MAXN] , u[MAXN] , v[MAXN] , w[MAXN] , ans[MAXN];
int cnt , head[MAXN];
bool vis[MAXN];
struct edge{
int to , nxt , w;
}e[MAXN];
void add(int u , int v , int w) {
e[++ cnt].to = v;
e[cnt].nxt = head[u];
e[cnt].w = w;
head[u] = cnt;
}
deque<int> q;
void Spfa() {
memset(dis , 0x3f , sizeof(dis));
dis[n + 1] = 0;
q.push_back(n + 1);
while(!q.empty()) {
int u = q.front();
q.pop_front();
for (int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].to;
if (dis[v] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
vis[v] ++;
if (vis[v] == n + 2) {
printf("No");
exit(0);
}
if (q.size() && dis[q.front()] >= dis[v]) q.push_front(v); // SLF 优化
else q.push_back(v);
}
}
}
}
int main() {
scanf("%d %d", &n , &m);
for (int i = 1 ; i <= m ; i ++) {
scanf("%d %d %d %d", &op[i] , &u[i] , &v[i] , &w[i]);
u[i] --;
}
for (int i = 0 ; i <= 20 ; i ++) { // 对二进制每一位分别处理
cnt = 0;
memset(head , 0 , sizeof(head));
for (int i = 0 ; i <= n ; i ++) add(n + 1 , i , i);
for (int j = 1 ; j <= m ; j ++) {
if (op[j] == 1) { // 依照限制条件连边
if ((w[j] >> i) & 1) add(v[j] , u[j] , -1);
else add(u[j] , v[j] , 0) , add(v[j] , u[j] , 0);
} else {
if ((w[j] >> i) & 1) add(u[j] , v[j] , v[j] - u[j]) , add(v[j] , u[j] , u[j] - v[j]);
else add(u[j] , v[j] , v[j] - u[j] - 1);
}
}
for (int j = 1 ; j <= n ; j ++) add(j , j - 1 , 0) , add(j - 1 , j , 1); // 前缀和数组本身条件
Spfa();
for (int j = 1 ; j <= n ; j ++) {
ans[j] += ((dis[j] - dis[j - 1]) << i);
}
}
for (int i = 1 ; i <= n ; i++) printf("%d ", ans[i]);
return 0;
}
Intervals
题意:在 [ 0 , 50000 ] [0,50000] [0,50000] 选出尽量少的整数,使每个区间 [ l i , r i ] [l_i,r_i] [li,ri] 内都有至少 x i x_i xi 个数被选出。
由于该题涉及了区间操作,较易想到前缀和。不妨令 p r e i pre_i prei 为 0 − i 0 - i 0−i 选出的数的个数,这可得以下不等式:
- 由于 [ l i , r i ] [l_i,r_i] [li,ri] 内都有至少 x i x_i xi 个数被选出,则 p r e r i − p r e l i − 1 ≥ x i pre_{r_i} - pre_{l_i - 1} \geq x_i preri−preli−1≥xi。
- 由于每个数只能被选一次,则 p r e i − p r e i − 1 ≤ 1 pre_i - pre_{i-1} \leq 1 prei−prei−1≤1。
- 根据前缀和本身的定义,则 p r e i ≥ p r e i − 1 pre_i \geq pre_{i-1} prei≥prei−1。
根据以上不等式,建立差分约束系统进行求解即可。
注意:
- 该题求最小值,所以是最长路。
- 该题无需将 [ 0 , 50000 ] [0,50000] [0,50000] 的数都建边,只需要对 [ m i n n , m a x n ] [\mathrm{minn} , \mathrm{maxn}] [minn,maxn] 进行处理即可,其中 m i n n \mathrm{minn} minn 为 l i l_i li 最小值, m a x n \mathrm{maxn} maxn 为 r i r_i ri 最大值。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 1e6 + 5;
int n , m , vis[MAXN] , cnt , head[MAXN] , ed;
int st = 0x3f3f3f3f , dis[MAXN];
struct edge{
int to , nxt , w;
}e[MAXN];
void add(int u , int v , int w) {
e[++ cnt].to = v;
e[cnt].nxt = head[u];
e[cnt].w = w;
head[u] = cnt;
}
void Spfa() { // 最长路
memset(dis , 0xcf , sizeof(dis));
dis[st] = 0;
queue<int> q;
q.push(st);
vis[st] = 1;
while(!q.empty()) {
int u = q.front();
q.pop();
vis[u] = 0;
for (int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].to;
if (dis[v] < dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
if (vis[v]) continue;
vis[v] = 1;
q.push(v);
}
}
}
}
int main() {
scanf("%d", &n);
for (int i = 1 , u , v , w ; i <= n ; i ++) {
scanf("%d %d %d", &u , &v , &w);
ed = max(ed , v + 1);
st = min(st , u);
add(u , v + 1 , w); // 建边
}
for (int i = st + 1 ; i <= ed ; i ++) add(i , i - 1 , -1) , add(i - 1 , i , 0);
Spfa();
printf("%d", dis[ed]); // dis[ed] 即为 0 ~ ed 选取的数的个数
return 0;
}
矩阵游戏
简化题意:给出一个 n - 1 行 m - 1 列的矩阵 b,令 b i , j = a i , j + a i , j + 1 + a i + 1 , j + a i + 1 , j + 1 b_{i,j} = a_{i,j}+a_{i,j+1}+a_{i+1,j}+a_{i+1,j+1} bi,j=ai,j+ai,j+1+ai+1,j+ai+1,j+1,求出满足条件的矩阵 a,满足矩阵中任意元素 0 ≤ a i , j ≤ 1000000 0 \leq a_{i,j} \leq 1000000 0≤ai,j≤1000000
不难发现,该题求出一个合法的 a 矩阵非常容易,不妨令 a 矩阵第一行第一列均为 0,即可求出合法解。但是该种做法,不一定满足 0 ≤ a i , j ≤ 1000000 0 \leq a_{i,j} \leq 1000000 0≤ai,j≤1000000 的限制条件。对于该种情况,考虑调整法。
调整法,是由一组解经过调整得到另一组合法解的方法。该题中,不妨将矩阵 a 每行元素交替加减 r i r_i ri,对每列元素也交替加减 c i c_i ci。这样便可保证 a 矩阵中每一个 2 × 2 2 \times 2 2×2 的矩阵元素和不变,即 b 矩阵不变。
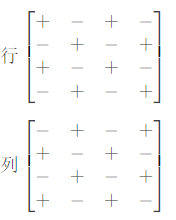
如上图所示,为何要 “交替” 呢?因为对于差分约束系统,只能处理形如 x i − x j ≤ x x_i - x_j \leq x xi−xj≤x 的不等式,而不能处理形如 x i + x j ≤ x x_i + x_j \leq x xi+xj≤x 的不等式。
有了调整方法,便可得出以下不等式:
- 对于 2 ∣ i + j 2 \mid \mathrm{i}+\mathrm{j} 2∣i+j, 0 ≤ a i , j + r i − c j ≤ 1000000 0 \leq a_{i,j}+r_i-c_j \leq 1000000 0≤ai,j+ri−cj≤1000000
- 对于 2 ∤ i + j 2 \nmid \mathrm{i}+\mathrm{j} 2∤i+j, 0 ≤ a i , j − r i + c j ≤ 1000000 0 \leq a_{i,j}-r_i+c_j \leq 1000000 0≤ai,j−ri+cj≤1000000
依照不等式建立差分约束系统,输出答案即可。由于该题是省选数据,需要加入 SLF 优化。
代码#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 1e3 + 5 , MAXM = 2e5 + 5;
int n , m , vis[MAXN] , cnt , T , head[MAXN] , tot[MAXN];
int a[MAXN][MAXN] , b[MAXN][MAXN];
ll dis[MAXN];
struct edge{
int to , nxt , w;
}e[MAXM];
void add(int u , int v , int w) {
e[++ cnt].to = v;
e[cnt].nxt = head[u];
e[cnt].w = w;
head[u] = cnt;
}
int Spfa() {
memset(dis , 0x3f , sizeof(dis));
memset(vis , 0 , sizeof(vis));
memset(tot , 0 , sizeof(tot));
dis[0] = 0;
deque<int> q;
q.push_back(0);
while(!q.empty()) {
int u = q.front();
q.pop_front();
vis[u] ++;
if (vis[u] > n + m) return 0;
tot[u] = 0;
for (int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].to;
if (dis[v] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
if (tot[v]) continue;
tot[v] = 1;
if (q.size() && dis[q.front()] >= dis[v]) q.push_front(v); //SLF优化
else q.push_back(v);
}
}
}
return 1;
}
int main() {
freopen("matrix.in" , "r" , stdin);
freopen("matrix.out" , "w" , stdout);
scanf("%d", &T);
while(T --) {
scanf("%d %d", &n , &m);
memset(a , 0 , sizeof(a));
for (int i = 1 ; i < n ; i ++) {
for (int j = 1 ; j < m ; j ++) {
scanf("%d", &b[i][j]);
}
}
for (int i = 2 ; i <= n ; i ++) { //求出一组解
for (int j = 2 ; j <= m ; j ++) {
a[i][j] = b[i - 1][j - 1] - a[i - 1][j] - a[i][j - 1] - a[i - 1][j - 1];
}
}
cnt = 0;
memset(head , 0 , sizeof(head));
for (int i = 1 ; i <= n ; i ++) {
for (int j = 1 ; j <= m ; j ++) {
if (i + j & 1){ // 建立差分约束系统
add(i , j + n , a[i][j]);
add(j + n , i , 1000000 - a[i][j]);
} else {
add(i , j + n , 1000000 - a[i][j]);
add(j + n , i , a[i][j]);
}
}
}
for (int i = 1 ; i <= n + m ; i ++) add(0 , i , 0); // 建立汇点
if (!Spfa()) puts("NO");
else {
puts("YES");
for(int i = 1 ; i <= n ; i ++) {
for(int j = 1 ; j <= m ; j ++) {
if(i + j & 1) a[i][j] = a[i][j] + dis[i] - dis[n + j];
else a[i][j] = a[i][j] - dis[i] + dis[n + j];
printf("%d ", a[i][j]);
}
puts("");
}
}
}
return 0;
}






















 656
656











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








