De Bruijn Sequence

A k-ary De Bruijn sequence of order n is a circular k-ary string containing every k-ary string of length n as a substring exactly once. Thus a De Bruijn sequence has length kⁿ. For n = 3 and k = 2, the lexicographically smallest De Bruijn sequence is 00010111.

如果k = 2, 则就叫binary De Bruijn sequence(下面简称DB序列). n阶的k叉DB序列： 长度为 kⁿ ，每个子串长度为n。从左到右按子串遍历，没有一个子串是重复的。

如n = 3 and k = 2 的DB序列00010111，从左到右按子串遍历：000， 001， 010， 101， 011， 111， 110， 100。 我们可以看到，这几个子串没有一个是重复的。

 

Every De Bruijn sequence corresponds to a Eulerian cycle on a De Bruijn graph, one of which is shown below (for n = 3 and k = 2).

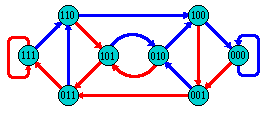
可以用DB图来构造DB序列，先构造DB图，然后找一个结点没有重复的回路就能构成DB序列。

以构造n = 3 and k = 2 的DB图为例：

step1: 写出所有可能的子串，如这里就是8种：000， 001， 010， 101， 011， 111， 110， 100

step2: 先摆好第一个结点，如000，它下一个子串的可能是000， 001；其中000是重复的，所以无需找它接下来的子串。我们看001，它下一个子串的可能是010， 011。 以此类推， 构成的图如上所示。

找结点没有重复的回路： 000， 001， 011， 111， 110， 101， 010， 100

故该回路对应的DB序列为：00011101。

 

At first glance De Bruijn sequences appear to have little to do with necklaces or Lyndon words. However, Fredericksen has proven that the lexicographic sequence of Lyndon words of lengths divisible by n gives the lexicographically least De Bruijn sequence, and that is the one output by our program.

The algorithm used is from the Combinatorial Generation book. It is a recursive algorithm and generates necklaces in lexicographic order, as does the first efficient necklace generation algorithm, the iterative algorithm of Fredricksen, Maiorana, and Kelsen.

 

Reference Website: http://www.theory.csc.uvic.ca/~cos/inf/neck/NecklaceInfo.html