二进制转换为十六进制数是
Prerequisite: Number systems
先决条件: 数字系统
Converting binary numbers into hexadecimal numbers is similar to the conversion of binary into octal, it just requires some modifications. The relationship between binary numbers and hexadecimal numbers is given as:
将二进制数转换为十六进制数类似于将二进制数 转换为八进制数 ,只需要进行一些修改即可。 二进制数和十六进制数之间的关系给出为:
| Decimal | Hexadecimal | Binary |
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
| 小数 | 十六进制 | 二元 |
| 0 | 0 | 0000 |
| 1个 | 1个 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | 一个 | 1010 |
| 11 | 乙 | 1011 |
| 12 | C | 1100 |
| 13 | d | 1101 |
| 14 | Ë | 1110 |
| 15 | F | 1111 |
In hexadecimal number system, we have sixteen digits ranging from 0 to 15 which can be represented using four-bit binary numbers in 24 = 16 ways, so starting from the least significant bit of the binary number, we group four successive bits of the binary number to get its equivalent hexadecimal number as seen from the table above.
在十六进制系统中,我们有十六个数字,范围从0到15 ,可以使用4位二进制数以2 4 = 16的方式表示,因此从二进制数的最低有效位开始,我们将二进制数的四个连续位分组从上表中可以看到二进制数以获取其等效的十六进制数。
In an integral part, the grouping of four bits is done from the right side to the left side whereas in the fractional part the grouping of four bits is done from left to right and then convert it to its equivalent hexadecimal symbol.
在整数部分中,四个位的分组是从右侧到左侧完成的,而在分数部分中,四个位的分组是从左到右进行的,然后将其转换为等效的十六进制符号。
In the process of grouping four bits, one/two/three bits can be added to the left of the MSB in an integral part and/or to the right of the LSB bit of the fractional part of the binary number.
在对四位进行分组的过程中,可以在二进制数的小数部分的整数部分的MSB左侧和/或LSB的右边添加一/二/三位。
Note: Whenever we need any additional bits, we only add '0' as the additional bit.
注:每当我们需要任何其他位时,我们仅将“ 0”添加为其他位。
Example 1: Convert (01111111.1010)2 to ( ? )16
示例1:将(01111111.1010) 2转换为(?) 16
Solution:
解:
We will make a grouping of 4 bits from right to left direction in an integral part and from left to right direction in the fractional part and then replace it with the corresponding symbol with the help of the table provided above.
我们将在一个整数部分中从右到左方向以及在分数部分中从左到右方向将4位分组,然后在上面提供的表格的帮助下将其替换为相应的符号。
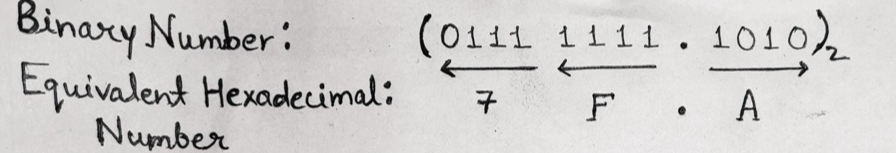
Therefore, (01111111.1010)2 = (7F. A)16
因此, (01111111.1010) 2 =(7F.A) 16
Example 2: Convert (1110011100.110001)2 to ( ? )16
示例2:将(1110011100.110001) 2转换为(?) 16
Solution:
解:
The given binary number consists of only 10 bits in an integral part and only 6 bits in the fractional part. So, making a group of 4 bits is not possible. In this case, we have to add bits from our side so that we can make a grouping of 4 bits. Thus, we add two zero bits at the LHS of the MSB in the integral part which will make 12 bits in an integral part, without disturbing its original value. Similarly, two zero bits are added to the RHS of the LSB in the fractional part, which will result in 8 bits in the fractional part and can be grouped in a group of 4 bits.
给定的二进制数在整数部分仅包含10位,在小数部分仅包含6位。 因此,不可能将4位组成一组。 在这种情况下,我们必须从自己的角度添加位,以便我们可以将4位分组。 因此,我们在整数部分的MSB的LHS处添加两个零位,这将在整数部分中形成12位,而不会干扰其原始值。 类似地,两个零位在小数部分被添加到LSB的RHS中,这将导致小数部分为8位,并且可以分为4位。
Thus, above given binary number can now be written as: (001110011100.11000100)2
因此,上述给定的二进制数现在可以写为: (001110011100.11000100) 2
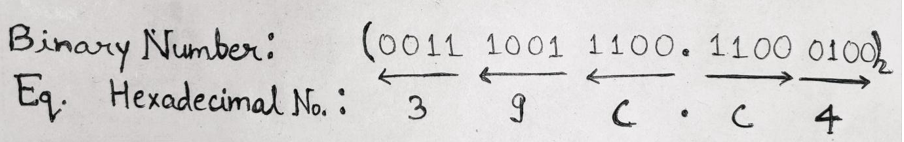
Therefore, (001110011100.11000100)2 = (39C.C4)16
因此, (001110011100.11000100) 2 =(39C.C4) 16
Example 3: Convert (100101011110.0110111)2 to ( ? )16
示例3:将(100101011110.0110111) 2转换为(?) 16
Solution:
解:
Given binary number has 12 bits in an integral part, so it can be easily grouped in a group of 4 bits but there are only 7 bits in the fractional part so we need to add one more additional zero bit to the RHS of LSB in the fractional part. Thus, the above binary number can now be written as: (100101011110.01101110)2
给定的二进制数在整数部分中具有12位,因此可以轻松地将其分为4位,但是小数部分中只有7位,因此我们需要在LSB的RHS的RHS中再增加一个零位。小数部分。 因此,上述二进制数现在可以写为: (100101011110.01101110) 2

Therefore, (100101011110.01101110)2 = (95E.6E)16
因此, (100101011110.01101110) 2 =(95E.6E) 16
二进制转换为十六进制数是























 4027
4027

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








