gg代码转xs代码工具_多余3（XS-3）代码和格雷代码

gg代码转xs代码工具

多余的3码 (Excess-3 Code)

Excess-3 Code is a non-weighted BCD (8421) Code. Excess-3 Code is derived from 8421 code by adding 0011 (3) to all code groups. It is a sequential code, thus can be also used for performing arithmetic operations. Also, Excess-3 codes are self-complementing codes in nature. Therefore, subtraction by the method of complement addition is more direct in the XS-3 code than in 8421 BCD code. Like, BCD code, it also has six invalid states which are: 0000, 0001, 0010, 1101, 1110 and 1111.

Excess-3代码是非加权BCD(8421)代码。 通过将0011(3)添加到所有代码组，从8421代码派生出Excess-3代码 。 它是一个顺序代码 ，因此也可以用于执行算术运算。 同样， 多余3码本质上是自补码 。 因此，与8421 BCD码相比，在XS-3码中用补码加法的减法更为直接。 像BCD代码一样，它也有六个无效状态，分别是： 0000、0001、0010、1101、1110和1111 。

Relationship between Decimal Numbers, Binary Numbers, and XS-3 Numbers can be given as,

十进制数，二进制数和XS-3数字之间的关系可以表示为：

Decimal Numbers	Binary Numbers	Excess-3 Code (Binary Number + 0011)
0	0000	0011
1	0001	0100
2	0010	0101
3	0011	1100
4	0100	0111
5	0101	1000
6	1010	1001
7	0111	1010
8	1000	1011
9	1001	1100

小数	二进制数	多余的3码(二进制数+ 0011)
0	0000	0011
1个	0001	0100
2	0010	0101
3	0011	1100
4	0100	0111
5	0101	1000
6	1010	1001
7	0111	1010
8	1000	1011
9	1001	1100

Example: Represent (1548)₁₀ in Excess-3 notation.

示例：用(Excess-3)表示(1548) ₁₀ 。

Solution:

解：

    1 = 0001 + 0011 = 0100	5 = 0101 + 0011 = 1000
    4 = 0100 + 0011 = 0111	8 = 1000 + 0011 = 1011

Therefore, (1548)₁₀ = 0100 1000 0111 1011 in XS-3 form.

因此，XS-3形式的(1548) ₁₀ = 0100 1000 0111 1011。

格雷码 (Gray Code)

The Gray Code is a non-weighted code and is cyclic as well. It is referred to as cyclic because successive code words in this code differ by only one bit-position i.e., it is a unit distance code. It is also reflective. In many practical applications such as analog to digital conversion, unit distance codes are used.

格雷码 是非加权码 ，也是循环的 。 之所以称为循环，是因为该代码中的连续代码字仅相差一个位位置，即它是一个单位距离代码。 这也是反射性的。 在许多实际应用中，例如模数转换，使用单位距离代码。

将二进制代码转换为格雷代码 (Conversion of Binary Code into Gray Code)

To convert Binary Code into Gray Code, one should have knowledge of truth table of XOR Gate which is as,

要将二进制代码转换为格雷代码，应了解XOR门的真值表，即

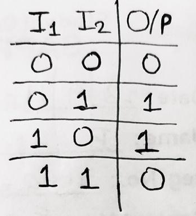
Now, the MSB of the binary number is copied as it is and then we perform XOR operation for consecutive bits in a pair of two.

现在，按原样复制二进制数的MSB，然后对两个成对的连续位执行XOR操作。

Example 1: Convert (1001)₂ into Gray Code.

示例1：将(1001) ₂转换为格雷码。

Solution:

解：

Therefore, (1001)₂ = (1101)_g in gray code.

因此，格雷码为(1001) ₂ =(1101) _g 。

Example 2: Convert (10)₁₀ into Gray Code.

示例2：将(10) ₁₀转换为格雷码。

Solution:

解：

Firstly, we convert decimal number to binary number and then convert binary to gray code.

首先，我们将十进制数转换为二进制数，然后将二进制数转换为格雷码。

Therefore (10)₁₀ = (1111)_g

因此(10) ₁₀ =(1111) _g

将格雷码转换为二进制数 (Conversion of Gray Code into Binary Number)

The MSB of Gray code is copied as it to be the MSB bit of binary number which is then XORed with the next bot of gray code, the result is recorded as the next bit of binary number, now this recorded bit is XORed with the next bit of gray code and this process is continued till the LSB is obtained.

将格雷码的MSB复制为二进制数的MSB位，然后将其与下一个格雷码机器人异或，将结果记录为二进制数的下一位，现在将该记录的位与下一个异或。位格雷码，此过程将一直持续到获得LSB。

Example 1: Convert (110011100)_g to binary number.

示例1：将(110011100) _g转换为二进制数。

Solution:

解：

Therefore, (110011100)_g = (10010111)₂

因此，(110011100) _g =(10010111) ₂

Example 2: Convert (101010101)_g to binary number.

示例2：将(101010101) _g转换为二进制数。

Solution:

解：

Therefore, (101010101)_g = (110011001)₂

因此，(101010101) _g =(110011001) ₂

翻译自: https://www.includehelp.com/basics/excess-3-xs-3-code-and-gray-code.aspx

gg代码转xs代码工具