二进制搜索法 java_Java中的二进制搜索

二进制搜索法 java

介绍 (Introduction)

In this tutorial, we are going to learn about the Binary Search algorithm and implement it in Java.

在本教程中，我们将学习二进制搜索算法并在Java中实现它。

Normal Linear or sequential search algorithm is convenient to use for a small set of data. When the size increases, then in the worst case we require 2ⁿ comparisons, where the size of an array or list is n.

常规线性或顺序搜索算法可方便地用于少量数据。 当大小增加时，在最坏的情况下，我们需要2 ^n个比较，其中数组或列表的大小为n 。

Thus we require more efficient algorithms for searching elements. In this tutorial, we are going to explore how binary search is a simple and efficient algorithm as well as how it works.

因此，我们需要更有效的算法来搜索元素。 在本教程中，我们将探讨二进制搜索是一种简单而有效的算法，以及它是如何工作的。

二元搜索的核心算法 (The Core Algorithm of Binary Search)

For Binary Search, the elements in an array must be in sorted order. Let us consider an array that is in ascending order. The Binary search compares elements to be searched, that is, the key with the element present in the middle of the data set. It is based on the following three(3) basic conditions:

对于二进制搜索， 数组中的元素必须按排序顺序。 让我们考虑一个升序的数组。 二进制搜索将要搜索的元素（即关键字）与数据集中中间的元素进行比较。 它基于以下三个（ 3 ）基本条件：

1. if the key is less than the middle element, then we now need to search only in the first half of the array,
   如果键小于中间元素，那么我们现在只需要在数组的前半部分搜索，
2. If the key is greater than the middle element, then we need to only search in the second half of the array,
   如果键大于中间元素，那么我们只需要在数组的后半部分搜索，
3. And if the key is equal to the middle element in the array, then the search ends,
   如果键等于数组中的中间元素，则搜索结束，
4. Finally, if the key is not found in the whole array, then it should return a none or -1. This indicates the element to be searched is not present.
   最后，如果在整个数组中找不到键，则应返回none或-1 。 这表明不存在要搜索的元素。

二进制搜索示例 (Example of Binary Search)

Consider a sorted array of 10 integers as given below,

考虑一个由10个整数组成的排序数组，如下所示，

Given Array

给定数组

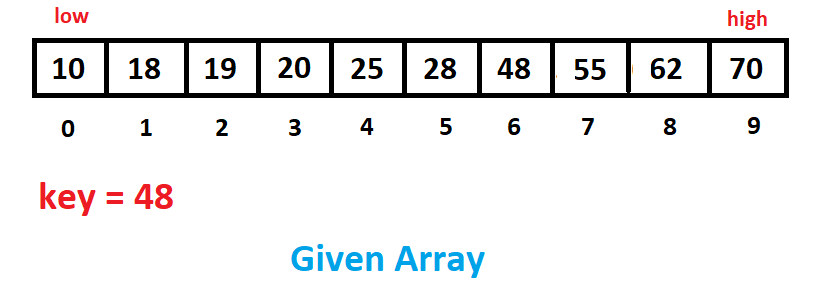
Suppose we are searching for the element 48. In this case, our key is 48.

假设我们正在搜索元素48 。 在这种情况下，我们的密钥是48 。

Figure 1

图1

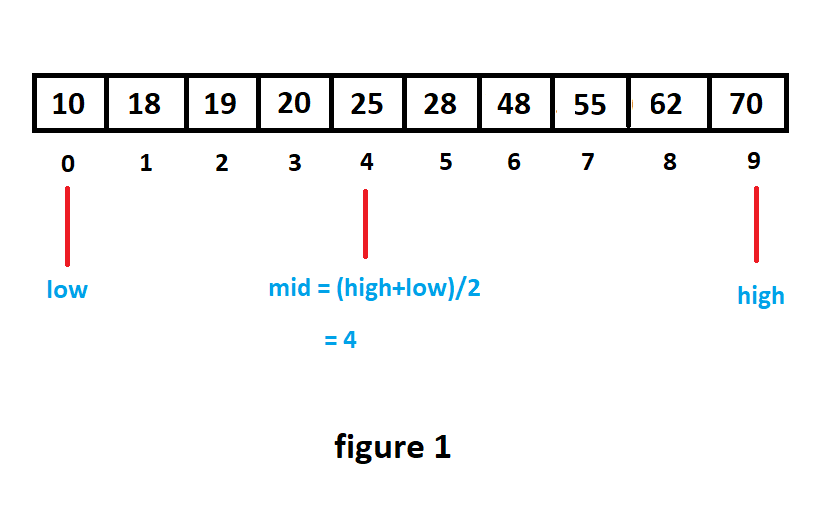
Now, we will have to compare the middle element, which is 25 with the element that we need to search(48). Since 48>25, we eliminate the first half and will have to search in the second half for the key.

现在，我们将比较中间的元素（即25）与我们需要搜索的元素（ 48 ）。 由于48>25 ，我们消除了前半部分，因此必须在后半部分中搜索密钥。

Further for doing that, we set low as Mid + 1 and high as the size of the array – 1 or, index of the last element.

为此，我们将低设置为Mid + 1 ，将高设置为数组的大小– 1或最后一个元素的索引。

Figure 2

图2

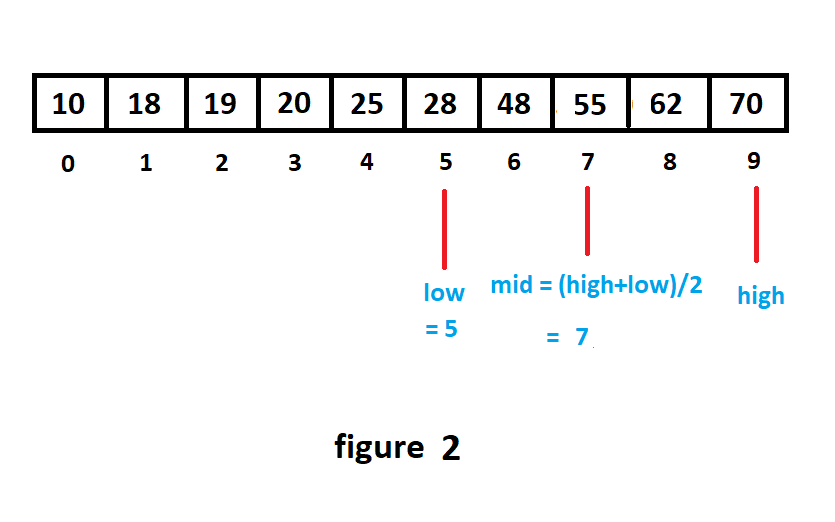
In the next iteration, we compare the middle element 55 with the key. Since 48<55, we will have to search the element again in the left half of the array. Correspondingly, the values of low and high are updated as 5(no change) and Mid – 1.

在下一次迭代中，我们将中间元素55与键进行比较。 由于48<55 ，我们将不得不在数组的左半部分再次搜索元素。 相应地，low和high的值更新为5 （不变）和Mid – 1 。

Figure 3

图3

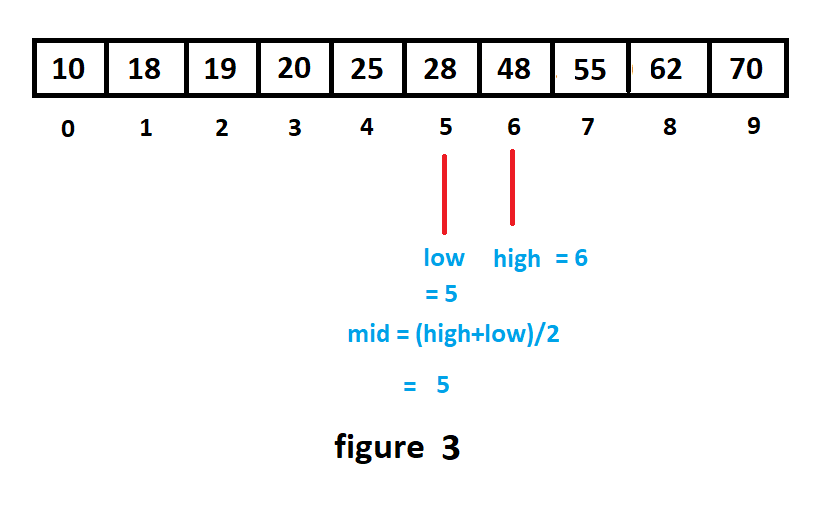
Nextly, now the middle element is 28 for which we have 48>28. Hence, we need to further consider the right portion of the array.

接下来，现在中间元素是28 ，因此我们有48>28 。 因此，我们需要进一步考虑数组的正确部分。

For which now, low = Mid + 1=6, and high = 6 (no change).

现在， 低=中+ 1 = 6 ， 高= 6 （无变化）。

Figure 4

图4

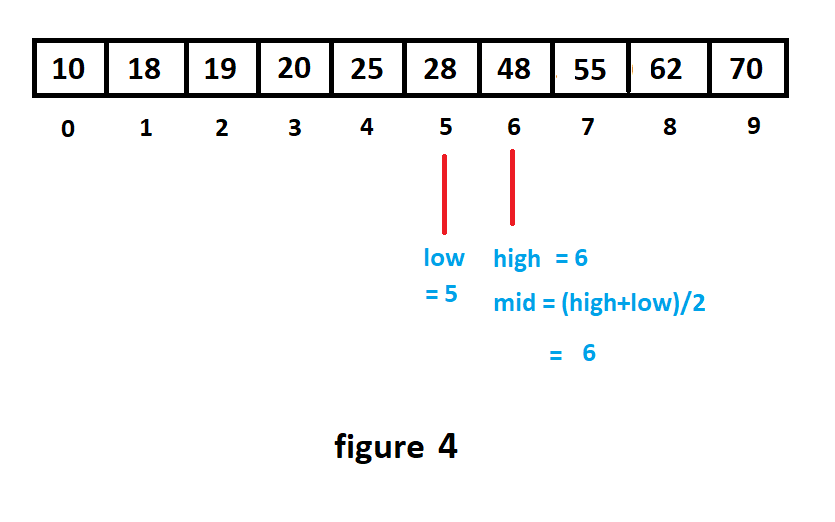
For the next iteration, the middle element is equal to the element to be searched, i.e., 48.

对于下一次迭代，中间元素等于要搜索的元素，即48 。

So, we found the number at index 6(Mid).

因此，我们在索引6（Mid）处找到了该数字。

用Java实现二进制搜索 (Implementing Binary Search in Java)

Now let us implement the above-mentioned Binary Search Algorithm in java.

现在让我们在Java中实现上述二进制搜索算法。

public class BinarySearch
{  
    public static int binarySearch(int arr[], int low, int high, int key)
    {  
        int mid = (low + high)/2;  
        while( low <= high )
        {  
            if ( arr[mid] < key )
            {  
                low = mid + 1;     
            }
            else if ( arr[mid] == key )
            {
                return mid;  
            }else
            {  
                high = mid - 1;  
            }  
            mid = (low + high)/2;  
        }  
        if ( low > high )
        {   
            return -1;
        }  
        return -1;
   }  
   public static void main(String args[])
   {  
        int arr[] = {10,18,19,20,25,28,48,55,62,70};  
        int key = 48;  
        int n=arr.length-1;  
        int index = binarySearch(arr,0,n,key);  
        System.out.println("The sorted array is: ");
        for(int i=0;i<n;i++)
        {
            System.out.print(arr[i] + " ");
        }
        System.out.println("\nElement to be searched: "+key);
        if (index == -1)  
            System.out.println("Unfortunately the Element is not found!");  
        else  
            System.out.println("The Element is found at the index: "+index);  
   }  
}  

Output:

输出 ：

Binary Search In Java

Java中的二进制搜索

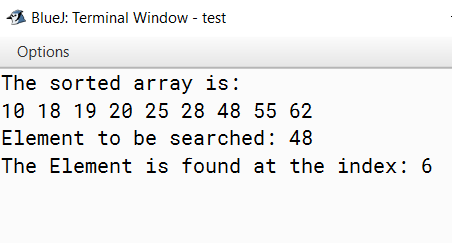
二进制搜索算法的复杂性 (Complexities of the Binary Search Algorithm)

The average number of comparisons for the binary search algorithm is log₂N. Hence, the time complexity of Binary Search is log₂n.

二分搜索算法的平均比较数为log ₂ N。 因此，二进制搜索的时间复杂度为log ₂ n 。

In terms of space complexity, for binary search, it is O(log n). In addition, it takes O(n) space to store the array.

就空间复杂度而言 ，对于二进制搜索，它是O（log n） 。 此外，存储阵列需要O（n）空间。

Where n is the size of the given sorted array.

其中n是给定排序数组的大小。

结论 (Conclusion)

So, in this tutorial, we learned about the Binary Search Algorithm and its implementation in Java. For clear understanding try out the code yourself. For any further questions feel free to use the comments below.

因此，在本教程中，我们学习了二进制搜索算法及其在Java中的实现。 为了清楚地理解，请自己尝试代码。 如有任何其他疑问，请随时使用以下评论。

参考资料 (References)

• Binary Search Wikipedia page,
  Binary Search Wikipedia页面，
• Binary Search Tree – Journal Dev Article.
  二进制搜索树 -期刊开发文章。

翻译自: https://www.journaldev.com/37407/binary-search-in-java

二进制搜索法 java