选择排序算法代码_选择排序算法

选择排序算法代码

Selection sort is conceptually the most simplest sorting algorithm. This algorithm will first find the smallest element in the array and swap it with the element in the first position, then it will find the second smallest element and swap it with the element in the second position, and it will keep on doing this until the entire array is sorted.

选择排序从概念上讲是最简单的排序算法。 该算法将首先在数组中找到最小的元素，然后将其与第一个位置的元素交换，然后将找到第二个最小的元素，并将其与第二个位置的元素交换，并将继续执行此操作直到整个数组被排序。

It is called selection sort because it repeatedly selects the next-smallest element and swaps it into the right place.

之所以称为选择排序，是因为它反复选择下一个最小的元素并将其交换到正确的位置。

选择排序如何工作？ (How Selection Sort Works?)

Following are the steps involved in selection sort(for sorting a given array in ascending order):

以下是选择排序所涉及的步骤(用于按给定的数组升序排序)：

1. Starting from the first element, we search the smallest element in the array, and replace it with the element in the first position.

   从第一个元素开始，我们搜索数组中最小的元素，并将其替换为第一个位置的元素。

2. We then move on to the second position, and look for smallest element present in the subarray, starting from index 1, till the last index.

   然后，我们移至第二个位置，寻找子数组中存在的最小元素，从索引1开始，直到最后一个索引。

3. We replace the element at the second position in the original array, or we can say at the first position in the subarray, with the second smallest element.

   我们将原始数组中第二个位置的元素替换为第二个最小元素，或者可以说在子数组中第一个位置。

4. This is repeated, until the array is completely sorted.

   重复此过程，直到将数组完全排序为止。

Let's consider an array with values {3, 6, 1, 8, 4, 5}

让我们考虑一个值{3, 6, 1, 8, 4, 5} 3，6，1，8，4，5 {3, 6, 1, 8, 4, 5}的数组

Below, we have a pictorial representation of how selection sort will sort the given array.

下面，我们以图形方式表示选择排序将如何对给定数组进行排序。

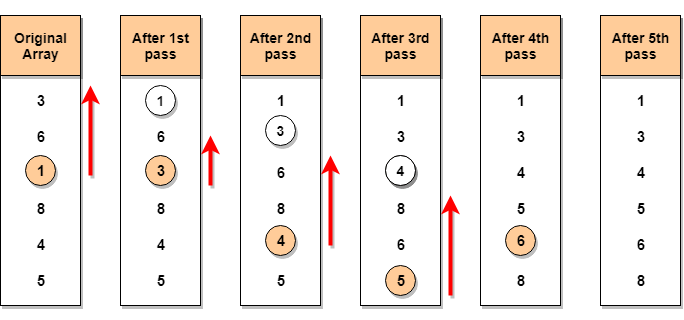
In the first pass, the smallest element will be 1, so it will be placed at the first position.

在第一遍中，最小的元素将是1 ，所以它会被放置在第一位置。

Then leaving the first element, next smallest element will be searched, from the remaining elements. We will get 3 as the smallest, so it will be then placed at the second position.

然后离开第一个元素，从剩余的元素中搜索下一个最小的元素。 我们将获得最小的3 ，因此将其放置在第二个位置。

Then leaving 1 and 3(because they are at the correct position), we will search for the next smallest element from the rest of the elements and put it at third position and keep doing this until array is sorted.

然后保留1和3 (因为它们在正确的位置)，我们将从其余元素中搜索下一个最小的元素，并将其放置在第三位置，并继续进行此操作，直到对数组进行排序为止。

在子数组中查找最小元素 (Finding Smallest Element in a subarray)

In selection sort, in the first step, we look for the smallest element in the array and replace it with the element at the first position. This seems doable, isn't it?

在选择排序中，第一步，我们寻找数组中最小的元素，并将其替换为第一位置的元素。 这似乎可行，不是吗？

Consider that you have an array with following values {3, 6, 1, 8, 4, 5}. Now as per selection sort, we will start from the first element and look for the smallest number in the array, which is 1 and we will find it at the index 2. Once the smallest number is found, it is swapped with the element at the first position.

考虑到您的数组具有以下值{3, 6, 1, 8, 4, 5} 。 现在，按照选择排序，我们将从第一个元素开始，寻找数组中的最小数字1 ，然后在索引 2处找到它。 找到最小的数字后，它将与第一个位置的元素交换。

Well, in the next iteration, we will have to look for the second smallest number in the array. How can we find the second smallest number? This one is tricky?

好吧，在下一次迭代中，我们将不得不寻找数组中第二小的数字。 我们如何找到第二小的数字？ 这个棘手吗？

If you look closely, we already have the smallest number/element at the first position, which is the right position for it and we do not have to move it anywhere now. So we can say, that the first element is sorted, but the elements to the right, starting from index 1 are not.

如果您仔细观察，我们已经在第一个位置上找到了最小的数量/元素，这是它的正确位置，并且我们现在不必将其移动到任何位置。 因此我们可以说，第一个元素已排序，但从索引1开始的右边元素却未排序。

So, we will now look for the smallest element in the subarray, starting from index 1, to the last index.

因此，我们现在将在子数组中寻找最小的元素，从索引1开始到最后一个索引。

Confused? Give it time to sink in.

困惑？ 给它时间沉没。

After we have found the second smallest element and replaced it with element on index 1(which is the second position in the array), we will have the first two positions of the array sorted.

找到第二个最小元素并将其替换为索引1上的元素(这是数组中的第二个位置)之后，我们将对数组的前两个位置进行排序。

Then we will work on the subarray, starting from index 2 now, and again looking for the smallest element in this subarray.

然后，我们将从子索引2开始处理子数组，然后再次寻找该子数组中的最小元素。

实现选择排序算法 (Implementing Selection Sort Algorithm)

In the C program below, we have tried to divide the program into small functions, so that it's easier fo you to understand which part is doing what.

在下面的C程序中，我们试图将程序分成几个小函数，这样您可以更轻松地了解哪个部分在做什么。

There are many different ways to implement selection sort algorithm, here is the one that we like:

实现选择排序算法的方式有很多，这是我们喜欢的一种：

// C program implementing Selection Sort
# include <stdio.h>

// function to swap elements at the given index values
void swap(int arr[], int firstIndex, int secondIndex) 
{   
    int temp;
    temp = arr[firstIndex];
    arr[firstIndex] = arr[secondIndex];
    arr[secondIndex] = temp;
}

// function to look for smallest element in the given subarray
int indexOfMinimum(int arr[], int startIndex, int n) 
{
    int minValue = arr[startIndex];
    int minIndex = startIndex;

    for(int i = minIndex + 1; i < n; i++) {
        if(arr[i] < minValue) 
        {
            minIndex = i;
            minValue = arr[i];
        }
    } 
    return minIndex;
}

void selectionSort(int arr[], int n) 
{
    for(int i = 0; i < n; i++) 
    {
        int index = indexOfMinimum(arr, i, n);
        swap(arr, i, index);
    }
    
}

void printArray(int arr[], int size)
{
    int i;
    for(i = 0; i < size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

int main()
{
    int arr[] = {46, 52, 21, 22, 11};
    int n = sizeof(arr)/sizeof(arr[0]);
    selectionSort(arr, n);
    printf("Sorted array: \n");
    printArray(arr, n);
    return 0;
}

Note: Selection sort is an unstable sort i.e it might change the occurrence of two similar elements in the list while sorting. But it can also work as a stable sort when it is implemented using linked list.

注意：选择排序是不稳定的排序，即， 排序时可能会更改列表中两个相似元素的出现。 但是，当使用链表实现时，它也可以作为稳定的排序。

选择排序的复杂度分析 (Complexity Analysis of Selection Sort)

Selection Sort requires two nested for loops to complete itself, one for loop is in the function selectionSort, and inside the first loop we are making a call to another function indexOfMinimum, which has the second(inner) for loop.

选择排序需要两个嵌套的for循环来完成自身，一个for循环在函数selectionSort ，并且在第一个循环内，我们调用另一个函数indexOfMinimum ，该函数具有第二个(内部) for循环。

Hence for a given input size of n, following will be the time and space complexity for selection sort algorithm:

因此，对于给定的输入大小n ，以下是选择排序算法的时间和空间复杂度：

Worst Case Time Complexity [ Big-O ]: O(n²)

最坏情况下的时间复杂度[Big-O]： O(n ² )

Best Case Time Complexity [Big-omega]: O(n²)

最佳情况时间复杂度[Big-Omega]： O(n ² )

Average Time Complexity [Big-theta]: O(n²)

平均时间复杂度[Big-theta]： O(n ² )

Space Complexity: O(1)

空间复杂度： O(1)

翻译自: https://www.studytonight.com/data-structures/selection-sorting

选择排序算法代码