作者 | yhc 编辑 | 自动驾驶之心
原文链接:https://zhuanlan.zhihu.com/p/687549139
点击下方卡片,关注“自动驾驶之心”公众号
>>点击进入→自动驾驶之心『3DGS』技术交流群
本文只做学术分享,如有侵权,联系删文
关注计算机视觉/图形学的朋友肯定早就听过Gaussian Splatting的大名,本文旨在分享笔者对Gaussian Splatting的理解。和大部分同类文章相比,本文
不会涉及任何(难以理解的)数学
从可微渲染(Differentiable Rendering)的角度进行思考,这也是笔者认为最能领会3DGS之优雅的切入点
从geometry的角度“抨击”3DGS,聊一聊在什么意义下3DGS是不好的
下面开始~
0. Gaussian Splatting是干啥的
一言以蔽之:Gaussian Splatting提出了一种三维表达(3D Gaussian)和配套的渲染方式(Splatting),能够1)迅速地重建现实世界中的场景 2)用重建的场景渲染新视角图片,速度特别快(实时渲染) 3)用重建的场景渲染新视角图片,看起来特别真实
对原文的teaser进行解释:
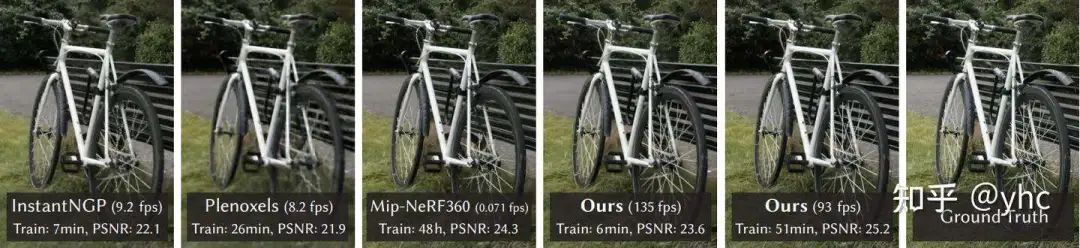
在这三个功能中,实时渲染的能力来自于对渲染过程的优化,本文不会过多深入;而“快速精准重建”的能力,来自于可微渲染——3DGS是一套高效的渲染框架,更是一套高效的可微渲染框架。
让我们先用一小节,理解一下可微渲染在解决什么样的问题。
1.高观点可微渲染:逆渲染和不连续
考虑一个通用的渲染过程:我们有一堆原料——物体(形状、材质、位置)和光照,将它们统一写作x;还有一个渲染器,它写作一个从“原料空间”到“图片空间”的函数f。那么任何一个正向渲染过程,就是根据原料,使用渲染器,求得一张图片(写作y)的过程,即y=f(x)。
逆渲染是这个过程的逆过程,给定一张图片 ,逆渲染希望通过某种手段,求出其对应的“原料”,这个目标可以写作 = ( )。
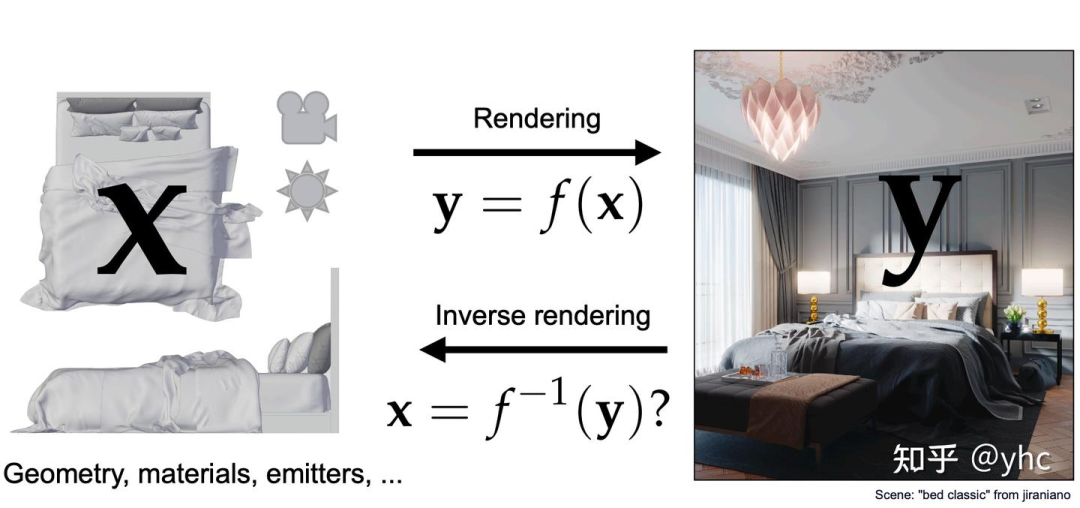
现实中,渲染过程的“逆过程”非常难以表达,如何想象光栅化的逆过程?但好在我们的目的并不是求出逆过程的表达式,而是用某种手段推测出 ,这只需要一个更松弛的条件—— ,有了它,我们就能用梯度下降等方式,不求逆过程表达式,一样能推测出正确的 。
到这里,相信读者也明白这里的某种手段是什么了,就是可微渲染!所谓可微渲染,指的就是这样一类正向渲染方法:其产生的图片对产生它的“原料”是可微的。更具体一点,就是指当某个“原料”的值(物体或光照)变化一点点时,能够知道图片上任何一个像素的颜色变化了多少,朝什么颜色变化。
可微渲染是通往逆渲染的可能途径,但这是条很不简单的途径,下面来介绍一下可微渲染的核心问题:不连续(后文会涉及3D Gaussian是怎么解决这个问题的)
想象一个简单的场景:两个三角形被渲染到了一张图片上,不考虑光照/shading,每个像素简单获得其对应的三角面颜色,那么这张图会像这样:

对于其中的每一个像素颜色,显然它与三角面颜色的映射关系不难建立:当三角面颜色变化一点时,与之对应的像素颜色都会发生对应的变化,在这个例子里,因为每个像素直接获取了三角面上的颜色,所以二者是相等的关系。我们当然可以通过梯度下降优化三角面颜色, 如果我们加入材质贴图,就能获得更强的表达能力,可以优化出各种图案。
一切似乎很简单,但是如果我们考虑优化这两个三角面的位置呢?
那我们需要知道,当三角形的位置移动一点时,每个像素的颜色应该怎么变,变多少。
这真的可能吗?我的意思是,导数真的存在吗?当三角形的位置移动一点时,像素的变化真的是连续的吗?
在这张图上,并不是!
考察三角形的边缘,我们放大一点来看,只看两个像素:

当红色三角形向右移动一个极小量时,有两种可能:
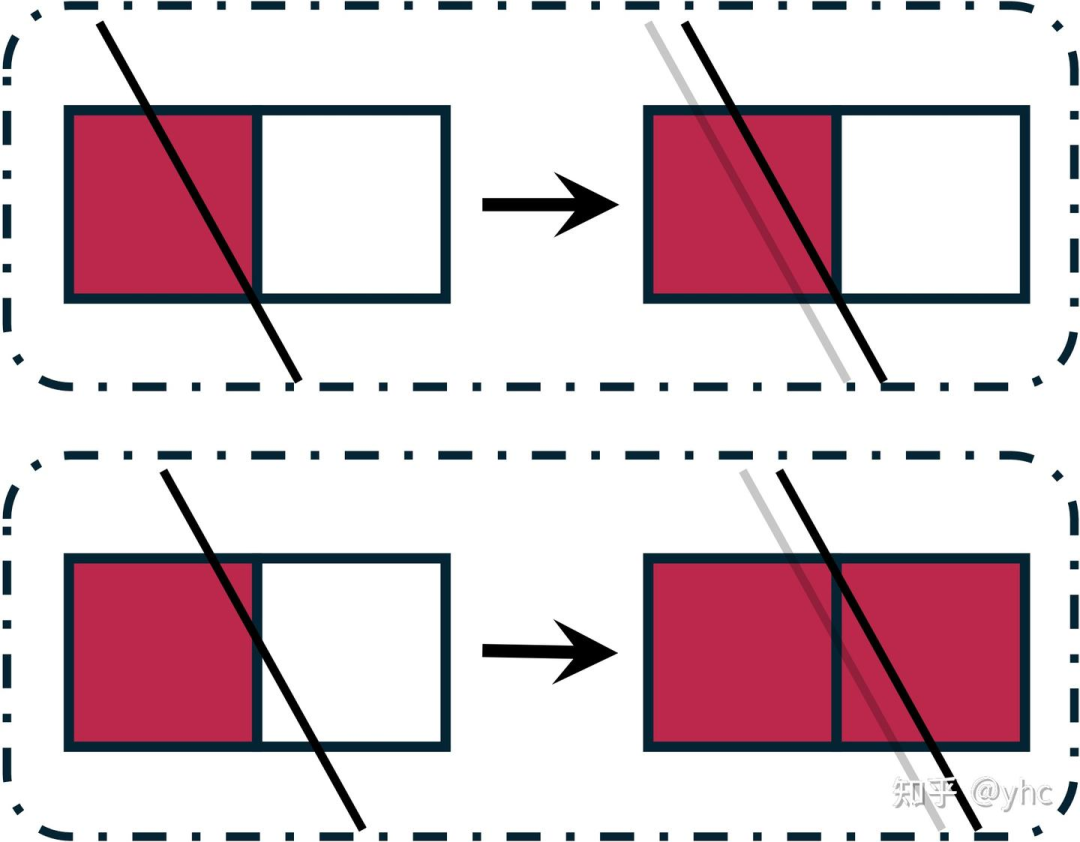
也就是说,对于右边这个像素来说,三角形向右的移动量-颜色的函数是这样:
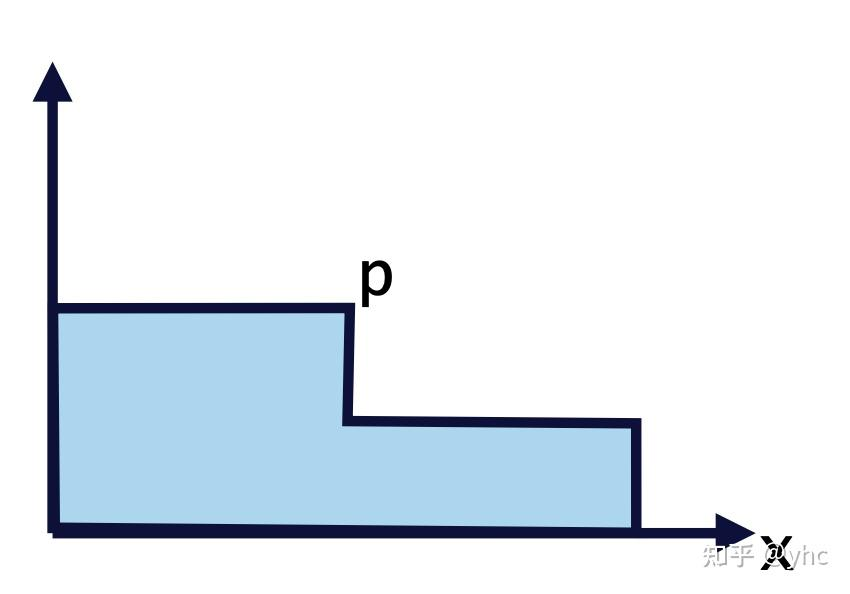
这个函数的导数在大部分位置是0,在其他所有位置上都不存在!
也就是说,当这个三角形移动一点时,我们不知道它的边缘上像素的颜色变化应该是多少,因为这个数字要么是0,要么不存在!
到这里,相信读者也明白了可微渲染的核心问题:位置“不可微”。
当然,这个问题实际上并非无解,因为位置并不是真的“不可微“。这里就不介绍其他可微渲染的解决方法了(如果大家想看请在评论区留言,可以开个新坑。
带着可微渲染的核心问题,下一章我们将进入Gaussian Splatting的世界
自动驾驶之心
论文辅导来啦

知识星球交流社区
近4000人的交流社区,近300+自动驾驶公司与科研结构加入!涉及30+自动驾驶技术栈学习路线,从0到一带你入门自动驾驶感知(大模型、端到端自动驾驶、世界模型、仿真闭环、3D检测、车道线、BEV感知、Occupancy、多传感器融合、多传感器标定、目标跟踪)、自动驾驶定位建图(SLAM、高精地图、局部在线地图)、自动驾驶规划控制/轨迹预测等领域技术方案、大模型,更有行业动态和岗位发布!欢迎加入。

独家专业课程
端到端自动驾驶、大模型、VLA、仿真测试、自动驾驶C++、BEV感知、BEV模型部署、BEV目标跟踪、毫米波雷达视觉融合、多传感器标定、多传感器融合、多模态3D目标检测、车道线检测、轨迹预测、在线高精地图、世界模型、点云3D目标检测、目标跟踪、Occupancy、CUDA与TensorRT模型部署、大模型与自动驾驶、NeRF、语义分割、自动驾驶仿真、传感器部署、决策规划、轨迹预测等多个方向学习视频
学习官网:www.zdjszx.com
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








