HDU5927 Auxiliary Set ->树形DP

题http://acm.hdu.edu.cn/showproblem.php?pid=5927

=====FROM:is_angon
题意：给一棵有根树，和m个“不重要”的点，但如果一个点是两个重要的点的最近公共祖先，它会变成重要的点。

思考：关键就是要知道每个不重要的点是否是某两个重要的点的lca；这个判断可以通过两次树dp来实现，第一次dp出每个节点有多少棵子树。

不难发现，只要节点node的某棵子树中含有一个重要的点，则这棵子树中一定含有一个点可以作为形成node为lca的其中一个点。（自己随便画一下很容易证明）

所以对给的m个点参照原图中的祖先关系新建一个图，即两个不重要的点a，b，如果a是b的祖先就连一条a指向b的边，否则不连（显然新图可能是不连通的）。

再在这个图上dp一次，求出每个节点有多少棵不含任何重要点的子树，用之前的一减，如果结果<2，说明这个点无法变成重要点，否则可以。
这里

=====

一开始往LCA上想，想到哭没搞出来
啊：
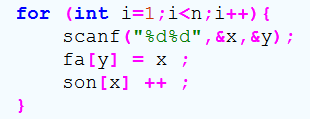
题目给的是一个图，要建双向边，我一开始以为是给的都是谁谁谁的father是谁的，
然后写出了这样的初始化

疯狂MLE，气死爸爸了
最后只能dfs建树，下次读题要仔细啊
下次看到题解别作死瞎优化

#include<map>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N = 100007;
map <int,int> vis;
vector<int>g[N],G[N];
int ask[N],ans,fa[N],son[N];
void DFS(int x,int dad){
    fa[x] = dad;
    son[x] = 0;
    for (int i= 0;i<g[x].size();i++){
        if (g[x][i]==dad)continue;
        DFS(g[x][i],x);
        son[x]++;
    }
}

int dfs(int x){
    if (vis[x]!=-1) return vis[x];
    int num = 0,sont=0;
    for(int i=0;i<G[x].size();i++)  {
        if( dfs(G[x][i]) >= 1 ) num++;
        sont++;
    }
    int sum = son[x] - sont + num ;
    if (sum>=2){ans++;return vis[x]=2;}
    else if (sum>=1)return vis[x] = 1 ;
    return vis[x] = -2 ;
}

int main(){
    //freopen("in.txt","r",stdin);
    int T,n,m,q,x,y;
    scanf("%d",&T);
    for (int cas=0;T--;){
        scanf("%d%d", &n, &q);
        memset(son,0,sizeof(son));
        for (int i=0;i<=n;i++)g[i].clear();
        for (int i=1;i<n;i++){
            scanf("%d%d",&x,&y);
            g[x].push_back(y);
            g[y].push_back(x);
        }
        DFS(1,0);
        printf("Case #%d:\n",++cas);
        for (;q--;){
            scanf("%d",&m);
            vis.clear();
            for (int i=1;i<=m;i++){
                scanf("%d",&ask[i]);
                vis[ask[i]] = -1;
                G[ask[i]].clear();
            }
            for (int i=1;i<=m;i++)
                if (vis[fa[ask[i]]]==-1)
                    G[fa[ask[i]]].push_back(ask[i]);
            ans = 0 ;
            for (int i=1;i<=m;i++)
                if (vis[ask[i]]==-1)dfs(ask[i]);
            printf("%d\n",n-m+ans);
        }
    }
    return 0;
}