纠删码(Erasure Code)及其演进LRC（Locally Repairable Codes）原理讲解

如何保证存储可靠性、数据可用性是大规模存储系统的难点和要点。数据冗余是保障存储可靠性、数据可用性的最有效手段，传统的冗余机制主要有副本（Replication）和纠删编码（Erasure Code，以下简称纠删码或EC，raid是纠删码一种特殊方式，不属于这里讨论的范畴）两种方式。

副本是将每个原始数据分块都镜像复制到另一存储介质上，从而保证在原始数据失效后，数据仍然可用并能通过副本数据恢复。在副本机制中，数据的可靠性和副本数是呈正相关，副本数越多，数据可用性越好，可靠性也越高，但也意味着更低的空间利用率以及更高的成本。在大规模存储系统中，节点出现故障并发生失效是一种大概率事件，这也就意味着双副本并不能满足企业对存储可靠性的需求，但三副本的存储开销太大，高达200%，且随着存储规模的增大，对存储系统的开销（如容量空间成本、运营成本等）都将显著增加。

相较于副本机制，纠删码机制具有更高的存储效率，在提供相同存储可靠性的条件下，可以最小化冗余存储开销。纠删码机制在网路环境下，其高存储效率的特性还能能显著降低网络中的数据流量，也就意味着在大规模存储系统中使用纠删码机制能够节约网路带宽和存储空间。所以在大规模存储的应用场景中，纠删码机制成了保证存储可靠性、数据可用性的最佳选择。

纠删码的原理：

纠删码的原理很简单，主要使用线性代数的方法,假设有四块：D1,D2,D3,D4，校验数据两块P1,P2.组成下面方程组：

（1）X1=D1

（2）X2=D2

（3）X3=D3

（4）X4=D4

（5）X1+X2+X3+X4=P1

（6）X1+2*X2+4*X3+8*X4=P2

根据上面的6个方程任意两个缺失都可以根据其他四个将丢失的两个计算出来。这就是纠删码的基本原理，当然在实现的时候不是直接使用方程组，实际应用是使用矩阵。

方程(1),(2),(3),(4)正好对应单位矩阵：

                                                                     

除此之外还有两个校验数据需要构造，一般使用范德蒙矩阵（使用柯西矩阵要快一些），为什么使用范德蒙矩阵是因为涉及到逆矩阵，只有当逆矩阵存在的前提下才可以恢复丢失的数据，而范德蒙矩阵恰好满足这个条件。我们的得到完整的编码矩阵：

                                                                     

编码：

编码就是根据编码矩阵，计算出校验数据，将校验数据和原始数据一起保存。

还是以上面为例，根据编码矩阵可以求得P1和P2：

                                         

应该注意的编码之后是原始数据块和校验数据块大小相同，因此这里的矩阵乘法是在伽罗华有限域（GF）内进行。简单来说，校验数据就是让P和所有或者部分原始数据都发生关系，这样在有数据块损坏时可以根据方程求解出损坏部分的数据。

解码：

假设有一个数据数据损坏，我们希望能用其他数据将损坏的部分恢复出来。最大允许损坏校验数据P个数这么多数据。

假设D4数据损坏：

1、 求解解码矩阵，在原编码矩阵中去掉对应损坏的数据那行，从上到下取n=4行，组成一个新矩阵这个矩阵就是解码矩阵： 

                                                                              

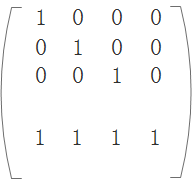
2、解码矩阵乘原始数据正好得到剩余完好的数据：

                                       

3、根据A*A-1=E，两边同乘解码矩阵的逆矩阵

                                       

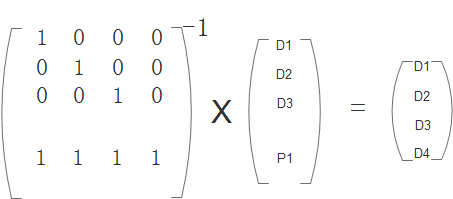
4、只要求出解码矩阵的逆矩阵即可求得损坏的数据D4

     求解逆矩阵首先要判断是否存在逆矩阵，判断逆矩阵是否存在的常用的两种方法：

1. 原矩阵的行列式的值是不等于0，这是由逆矩阵定义可知。
2. 原矩阵的秩等于矩阵阶数。

上面说了我们使用的是范德蒙矩阵，因此必然是存在逆矩阵的。

如果D4和P1同时损坏，根据上面的介绍，我们先求解出D4，然后在求解出P1即可。

根据上面看到的恢复损坏数据方法，我们可以看到当需要求解一个损坏数据时，需要拉取其数据块个数个数据，对于网络和cpu都是巨大的消耗。因此，有大牛就将优化的思路自然聚集到更容易出现的单个磁盘故障上来，如何更有效的处理这种概率较大的事件呢，直接出现的对策就是分组，把单个磁盘故障影响范围缩小到各个组内部，出坏盘故障时，该组内部解决，在恢复过程中读组内更少的盘，跑更少的网络流量，从而减小对全局的影响。

LRC

LRC（Locally Repairable Codes），是一种局部校验编码方法，其核心思想为：将校验块（parity block）分为全局校验块(global parity)、局部校验块(local reconstruction parity)，故障恢复时分组计算。

根据LRC的思想我们将上面的例子重新改造一番，分成两个组：

                         

P1=D1+D2

P2=D3+D4

P3= D1+D2+ D3+D4

P1、P2是局部校验。P3是全局校验。

当仅损坏一个数据块时，可以根据该数据在所在的分组，在组内对该数据块进行重建。损坏一个数据块时的最差情况就是全局校验块损坏，此时需要读全部数据块数据进行重建。

当损坏两个数据块时情况分成组内和组外，不管哪种需要拉取全部数据进行重建，此时采用LRC方法并不能提升性能。

当损坏三块数据时，如果这三个数据块在一个组内，例如P1、D1、D2。此时就无法进行数据重建，虽然我们这里是使用三个校验。

所以LRC并不是100%保证数据不丢，并且还要多占用一部分存储空间，一切事情都是有两面性的，顾此就要失彼，但是总的来说LRC还是很有竞争力的技术。