二叉树OJ——递归的暴力美学

原创已于 2025-06-27 11:51:12 修改 · 1.3k 阅读

30 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法 #二叉树 #递归 #c语言

于 2025-06-22 17:44:15 首次发布

初阶数据结构与算法专栏收录该内容

9 篇文章

订阅专栏

1.二叉树的前序遍历

144. 二叉树的前序遍历 - 力扣（LeetCode）

解题思路

题目要求前序遍历且要把遍历到的数据存放入一个数组里并返回，函数中给了两个参数，一个是二叉树的根结点，另一个是二叉树的结点个数，因此除了遍历之外还得求出结点个数，且知道结点个数了我们才能知道给数组开辟多大的空间，以足够放入二叉树中全部结点的数据。我们分为以下三个步骤进行。

1.先求出二叉树中结点的个数：求结点个数的功能在前文链式二叉树中已实现，这里解释代码逻辑

int BinaryTreeNodeSize(TreeNode*root)
 {
    if(root == NULL)
    {
        return 0;
    }
    return 1 + BinaryTreeNodeSize(root->left) + BinaryTreeNodeSize(root->right);
 }

二叉树结点个数 = 根结点 + 左子树结点个数 + 右子树结点个数

如果根结点为空，则直接返回0，因为为空时结点个数肯定为0，如果不为空，则根结点算1个，再加上左右子树的结点个数，此时将左右孩子参数传入该函数中进行递归，那么左右孩子相当于新的根结点，如果左孩子不为空，则加上本身再让其左右孩子继续递归，如果最后孩子结点为空，则返回0，函数栈帧销毁，然后往回递归，继续进入右孩子的递归函数.... 直到最后左右孩子都递归完成，即可计算出二叉树共有几个结点。

2.开辟*returnSize个int类型大小的数组空间

 *returnSize = BinaryTreeNodeSize(root);
    //开辟*returnSize个int空间的数组
    int*arr = (int*)malloc(sizeof(int)*(*returnSize));

将求结点个数的函数返回值赋给*returnSize，然后直接malloc申请即可。

3.前序遍历并赋值给数组

void preOrder(TreeNode* root, int* arr, int* pi)
{
    if(root == NULL)
    {
        return;
    }
    arr[(*pi)++] = root->val;
    preOrder(root->left, arr, pi);
    preOrder(root->right, arr, pi);
}

函数的实现需要传入三个参数：根结点、数组名以及数组下标（特别注意数组下标一定要传地址！）。如果根结点为空，则直接返回，销毁函数栈帧，这也是递归的结束条件。前序遍历的顺序——根左右，因此先把根结点放入数组中，然后下标（*pi）++，然后开始对左右子树依次进行递归，直到二叉树的结点数据按照“根左右”的顺序放入数组。

完成这三个步骤之后，直接将数组返回即可。

完整可执行通过代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

 typedef struct TreeNode TreeNode;

 int BinaryTreeNodeSize(TreeNode*root)
 {
    if(root == NULL)
    {
        return 0;
    }
    return 1 + BinaryTreeNodeSize(root->left) + BinaryTreeNodeSize(root->right);
 }

void preOrder(TreeNode* root, int* arr, int* pi)
{
    if(root == NULL)
    {
        return;
    }
    arr[(*pi)++] = root->val;
    preOrder(root->left, arr, pi);
    preOrder(root->right, arr, pi);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    //计算二叉树的结点个数
    *returnSize = BinaryTreeNodeSize(root);
    //开辟*returnSize个int空间的数组
    int*arr = (int*)malloc(sizeof(int)*(*returnSize));
    //将前序遍历的数放入数组中
    int i = 0;
    preOrder(root ,arr , &i);
    return arr;
}

2.二叉树的中序遍历

94. 二叉树的中序遍历 - 力扣（LeetCode）

解题思路

本题的思路基本同上，步骤也几乎相同，唯一不同的是中序遍历的遍历顺序与前序遍历不同

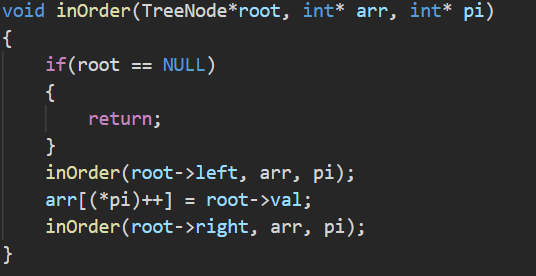
中序遍历的顺序为“左根右”，故优先往左子树向下递归，然后“触底反弹”（遍历到NULL）后return再将根结点放入数组中，之后递归右子树，顺序上有差异，这是唯一的不同。

完整可执行通过代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

 typedef struct TreeNode TreeNode;

int BinaryTreeSize(TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

void inOrder(TreeNode*root, int* arr, int* pi)
{
    if(root == NULL)
    {
        return;
    }
    inOrder(root->left, arr, pi);
    arr[(*pi)++] = root->val;
    inOrder(root->right, arr, pi);
}

int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    //计算二叉树结点个数
    *returnSize = BinaryTreeSize(root);
    //开辟数组空间
    int* arr = (int*)malloc(sizeof(int)*(*returnSize));
    //中序遍历
    int i = 0;
    inOrder(root, arr, &i);

    return arr;
}

3.二叉树的后序遍历

145. 二叉树的后序遍历 - 力扣（LeetCode）

解题思路

思路也同前序和中序遍历，只是遍历顺序不同。

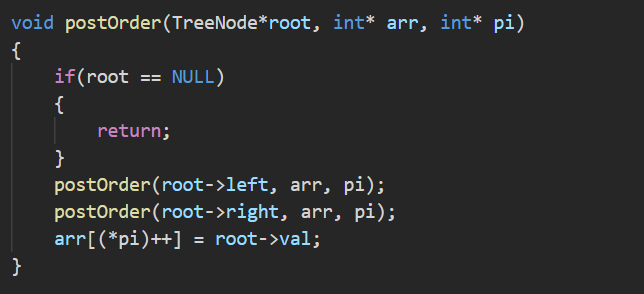
后续遍历的顺序为“左右根”，故优先递归向下遍历左子树再向下遍历右子树，子树递归回根结点之后才将根结点数据放入数组中。（递归到叶子结点的左右孩子时，由于孩子均为NULL，故全部递归返回叶结点并把叶结点数据放入数组中）

完整可执行通过代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 typedef struct TreeNode TreeNode;

int BinaryTreeSize(TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

void postOrder(TreeNode*root, int* arr, int* pi)
{
    if(root == NULL)
    {
        return;
    }
    postOrder(root->left, arr, pi);
    postOrder(root->right, arr, pi);
    arr[(*pi)++] = root->val;
}

int* postorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = BinaryTreeSize(root);
    int* arr = (int*)malloc(sizeof(int)*(*returnSize));
    int i = 0;
    postOrder(root, arr, &i);
    return arr;
}

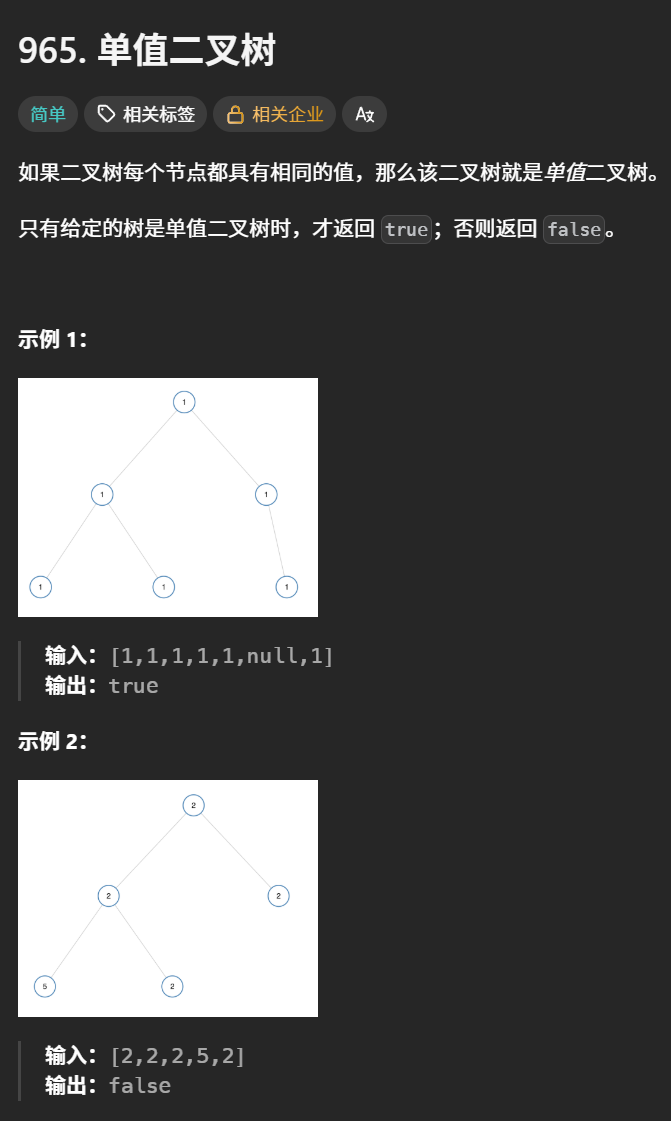
4.单值二叉树

965. 单值二叉树 - 力扣（LeetCode）

解题思路

判断二叉树中所有结点的值是否为同一个值，最底层的递归逻辑就是根结点的值与左右结点的值是否一致，当然还得考虑根结点为空的情况，这也是递归的终止条件，如果根结点为NULL，那不存在任何值，当然也算单值，则返回true。除此之外，还需单独比较根结点与左右孩子的值，但前提是左右孩子不为空。如果与左右孩子任意一个的值不一致，则直接返回false；如果均一致，则继续向下递归。递归完所有结点（左右子树）后均未出现false，则证明二叉树为单值二叉树。

完整可执行通过代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isUnivalTree(struct TreeNode* root) {
    if(root == NULL)
    {
        return true;
    }
    //值与左孩子不一致，直接返回false
    if(root->left && root->val != root->left->val)
    {
        return false;
    }
    //值与右孩子不一致，直接返回false
    if(root->right && root->val != root->right->val)
    {
        return false;
    }
    
    //左右子树递归均为true则为true，出现false则不是单值二叉树
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

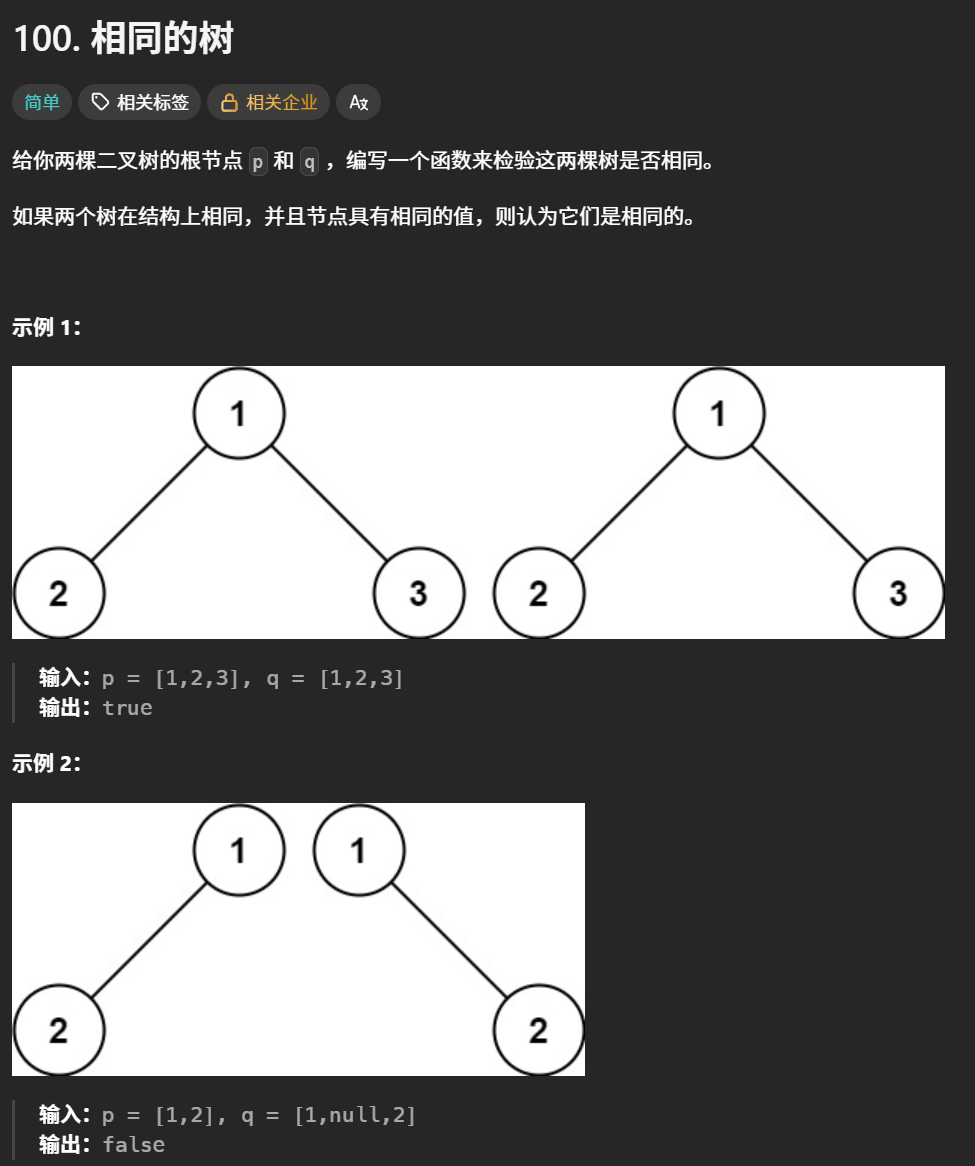
5.相同的树

100. 相同的树 - 力扣（LeetCode）

解题思路

要判断两棵树是否为相同的数，则需判断它们所有结点的结构和值是否相同，这里递归的底层逻辑就是判断两个结点的结构是否相同（是否要么均为空要么均不为空）和值是否相同，然后再分别向左右子树递归，判断所有结点，左子树跟左子树比，右子树跟右子树比。只要存在一处地方不同，则直接返回false，全相同才为true。

完整可执行通过代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    //pq均为空
    if(p == NULL && q == NULL)
    {
        return true;
    }
    //其中一个为空
    if(p == NULL || q == NULL)
    {
        return false;
    }
    //均不为空
    if(p->val != q->val)
    {
        return false;
    }

    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

6.对称二叉树

101. 对称二叉树 - 力扣（LeetCode）

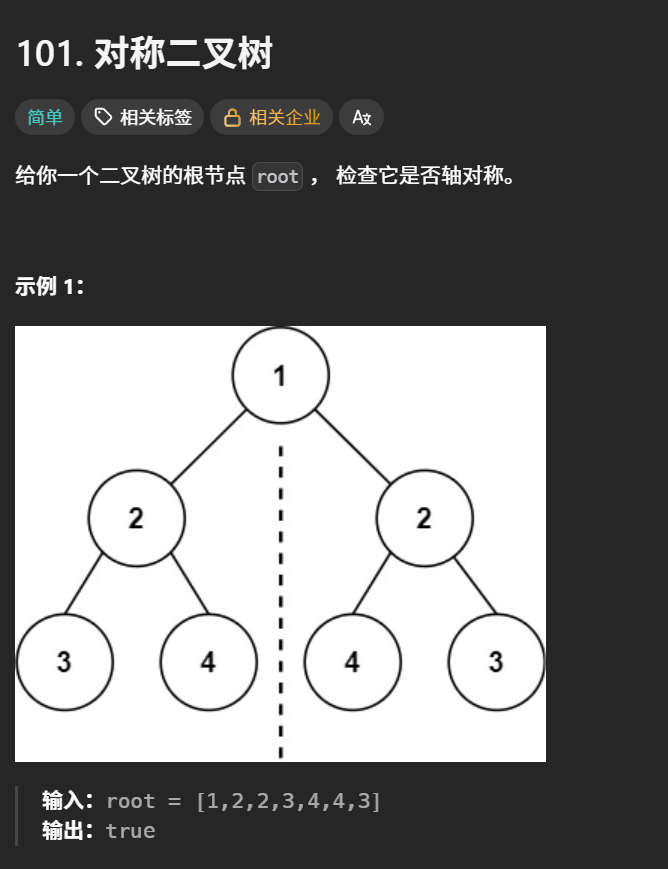
解题思路

本题解题方法与上一题“相同的树”有异曲同工之处，想要判断二叉树是否为对称二叉树，不必理会根结点，只需要判断左右子树是否对称即可，可以把左右子树看出两棵单独存在的树，上一题判断两棵树是否相同的方法就是在结构和数值上左子树跟左子树比、右子树跟右子树比，这题稍微有点变化

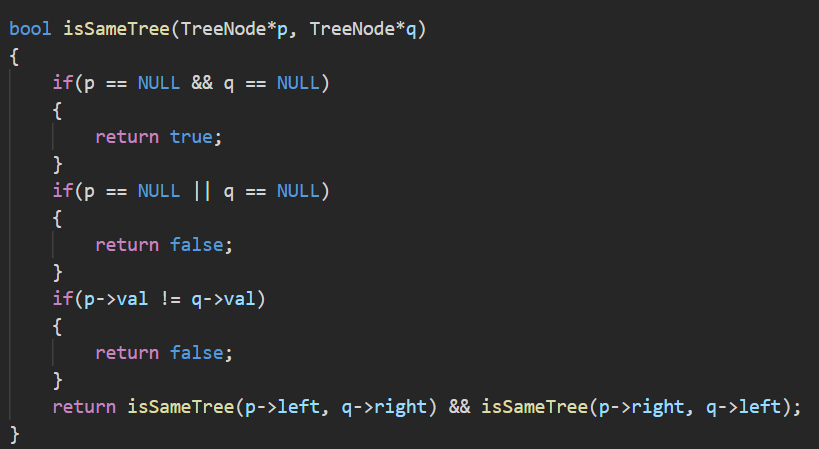
因为两棵子树要对称，因此最后一步递归传参时，我们不再是左跟左比、右跟右比，而是一棵树的左子树和另一棵树的右子树比，右子树与左子树比。改造封装好函数后，直接调用，将根结点的左右孩子传过去，便相当于传了两棵树的根结点，然后按照刚才的思路比对再返回函数的判断结果即可。

完整可执行通过代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

typedef struct TreeNode TreeNode;

bool isSameTree(TreeNode*p, TreeNode*q)
{
    if(p == NULL && q == NULL)
    {
        return true;
    }
    if(p == NULL || q == NULL)
    {
        return false;
    }
    if(p->val != q->val)
    {
        return false;
    }
    return isSameTree(p->left, q->right) && isSameTree(p->right, q->left);
}

bool isSymmetric(struct TreeNode* root) {
    return isSameTree(root->left, root->right);
}

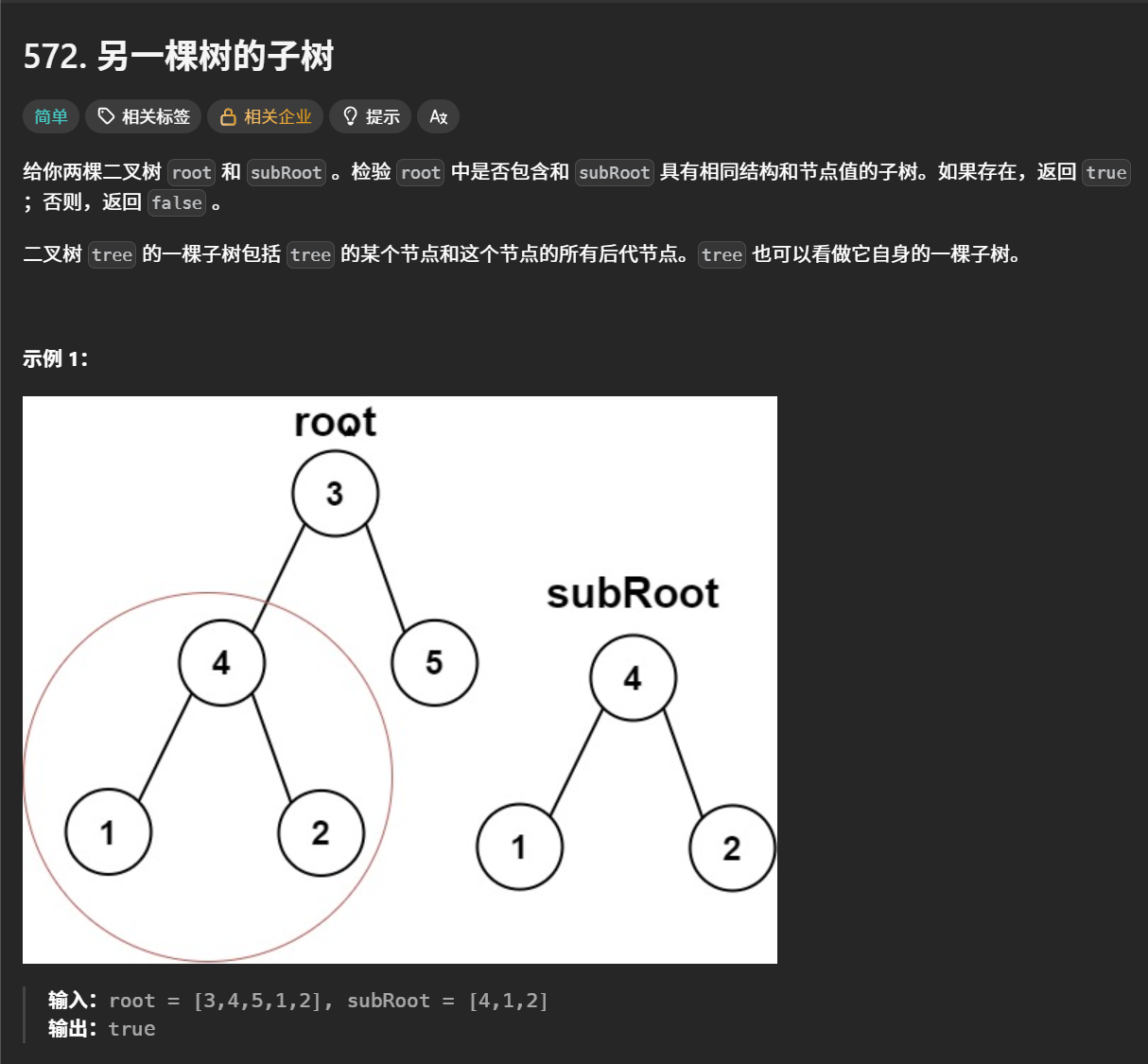
7.另一棵树的子树

572. 另一棵树的子树 - 力扣（LeetCode）

解题思路

要从一棵树中寻找与subRoot相同的树，本质上也是找相同的树，首先判断root是否为空，如果为空则直接返回false，因为空树不可能存在子树与subRoot相同。如果不为空，该题递归的底层逻辑就是将根结点root和subRoot传参到判断“相同的树”的函数isSameTree中（前面有代码实现了），如果这个root结点传过去后返回true则证明存在与subRoot相同的子树，如果返回false，则继续往左右子树向下递归，再继续传参匹配，直到出现可以匹配的子树（只要左右子树任意位置存在可与之匹配的子树即可）。

完整可执行通过代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

typedef struct TreeNode TreeNode;

bool isSameTree(TreeNode* p, TreeNode* q)
{
    if(p == NULL && q == NULL)
    {
        return true;
    }
    if(p == NULL || q == NULL)
    {
        return false;
    }
    if(p->val != q->val)
    {
        return false;
    }
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
    if(root == NULL)
    {
        return false;
    }
    if(isSameTree(root, subRoot))
    {
        return true;
    }
    return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

8.二叉树的构建及遍历

二叉树遍历_牛客题霸_牛客网

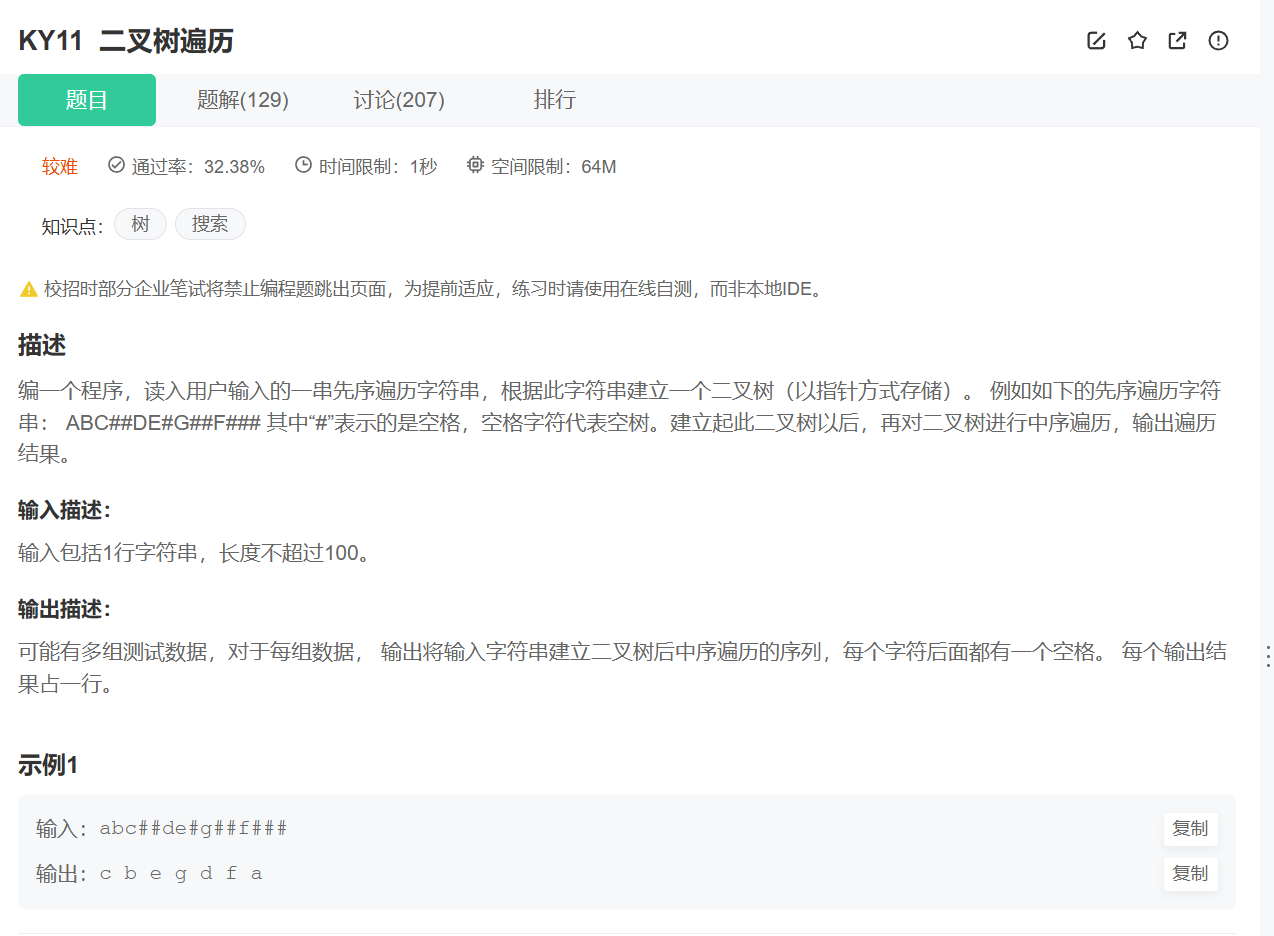
解题思路

主要思路就是先定义结点结构体，然后构建二叉树并传回根结点用结构体指针root接收，有了根结点，即可完成中序遍历。

首先在main函数里面创建好数组，由于题目已经告诉我们输入的字符串长度不超过100，因此我们创建静态数组给定100的空间即可，创建下标变量i，传入构建二叉树的函数createTree，并用root接收根结点。

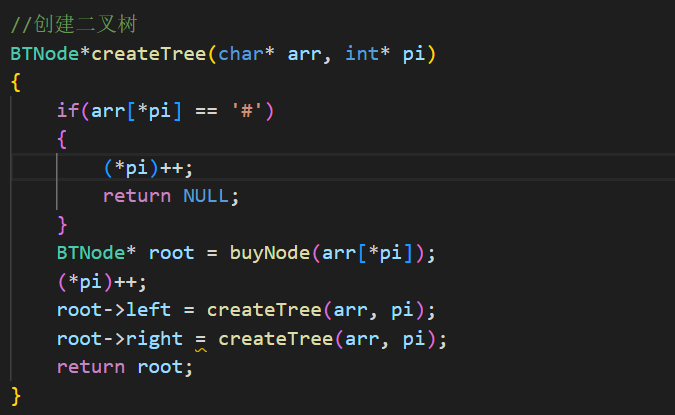
题目告诉我们'#'代表空格表示空树，因此当我们对数组遍历时遍历到该符号就无需创建结点，直接返回NULL即可，但是返回前记得让下标前进，即(*pi)++，否则无法继续遍历。遍历到其他字符时，便可以创建结点，将字符传参入申请结点的函数buyNode（申请结点的函数这里不单独展示了），并用root接收新创建的结点。由于题目说字符串是由二叉树前序遍历而来，因此我们先给根结点创建，再分别对左右子树递归创建结点，分别用root的左右孩子接收，最后字符串遍历结束，二叉树也创建完成，返回根结点。

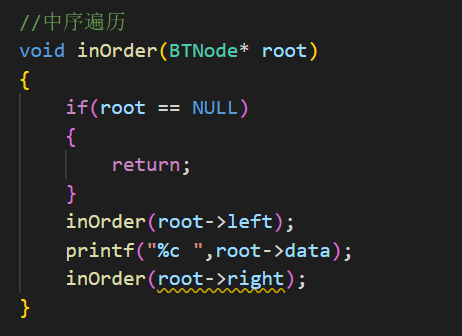
最后将main函数中接收到根结点的root传入中序遍历函数中即可，需要注意的是题目要求打印的每个字符之间需要留有空格，因此%c后面要有空格

完整可执行通过代码

#include<stdio.h>
#include<stdlib.h>

//构建链式二叉树
typedef struct BinaryTreeNode
{
    char data;
    struct BinaryTreeNode* left;
    struct BimaryTreeNode* right;
}BTNode;

//申请结点空间
BTNode* buyNode(char ch)
{
    BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
    newNode->data = ch;
    newNode->left = newNode->right = NULL;
    return newNode;
}

//创建二叉树
BTNode*createTree(char* arr, int* pi)
{
    if(arr[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }
    BTNode* root = buyNode(arr[*pi]);
    (*pi)++;
    root->left = createTree(arr, pi);
    root->right = createTree(arr, pi);
    return root;
}

//中序遍历
void inOrder(BTNode* root)
{
    if(root == NULL)
    {
        return;
    }
    inOrder(root->left);
    printf("%c ",root->data);
    inOrder(root->right);
}

int main()
{
    char arr[100];
    scanf("%s",arr);
    int i = 0;
    BTNode* root = createTree(arr, &i);
    inOrder(root);
    return 0;
}