更高效的有界KDM安全加密

更高效的有界KDM安全加密

1 引言

1.1 背景

密钥相关消息（KDM）安全已被许多研究人员广泛研究。一个KDM安全的加密方案E即使在使用相应的公钥 pk对密钥 sk进行加密时也能提供安全性。更一般地，关于函数集合 F的KDM安全加密方案E，即使对于任意函数 f ∈ F，使用用户 j ∈{1,…, }的公钥 pkj对 f(sk1,…, sk)进行加密时仍能保证安全性，其中 ski是用户 i对应于 i= 1,…, ,的密钥。

博内等人 [5]在标准模型下提出了首个称为BHHO加密方案的KDM安全公钥加密方案。该方案在DDH假设下对所有“指数上的仿射函数”集合是KDM安全的。

那么一个自然的问题是“我们能否构造一个关于所有函数集合的KDM安全加密方案？”巴拉克等人[4]通过证明存在一个关于所有具有任意固定电路大小的函数集合的KDM安全加密方案，肯定地解决了这个问题。此类加密方案被称为有界 KDM安全。巴拉克等人在DDH假设或LWE假设下构造了一个有界 KDM安全加密方案。

另一方面，如果一个函数的每个输出位至多依赖于一个输入位，则该函数称为投影。如果一个加密方案关于所有投影函数的集合是KDM安全的，则称该加密方案为投影 KDM安全。阿佩尔鲍姆[1]表明，可以从投影KDM安全加密方案获得有界KDM安全加密方案。

Bellare等人[6]随后展示了一种从混淆方案Ga和投影KDM安全加密方案 E构建有界KDM安全加密方案的简洁方法。他们的方案比[1,4]的方案更高效。（参见[6,图 20]进行比较。）1然而，密文大小仍然非常大。

总之，已知可以从投影KDM安全性获得有界KDM安全性。然而，密文大小非常大。

1.2 我们的贡献

在本文中，我们首先证明了有界KDM安全性可以从比投影KDM安全性弱得多的KDM安全性中获得。基于此，我们在各种假设下提出了比Bellare等人[6]更高效的有界KDM安全加密方案构造方法。

在Bellare等人的方案中， f(sk1,…, sk)的密文由(F, Y)组成，其中 F是一个混淆电路， Y是一个投影KDM安全加密方案 E的密文。我们的方案具有相同的结构，但要求 E只需满足较弱的KDM安全性。（更准确地说，我们所要求的弱KDM安全性与底层的混淆方案Ga相关。） 因此，我们的 Y的大小比Bellare等人[6],小 k倍，其中 k是安全参数。进一步假设f（sk1,…, sk）的门数量为 O(k)。则在DDH假设下，我们方案的密文总大小为 O(k3)，而在Bellare等人的方案[6],中为 O(k4)，其中两个方案均使用BHHO加密方案。

可以从任意关于仿射（指数上）函数集合的KDM安全加密方案构造出一个投影KDM安全加密方案，其中密钥被视为一个比特串。2我们也可以从此类加密方案构造出我们的弱KDM安全加密方案。

– 如上所述，BHHO加密方案在DDH假设下相对于“指数上的仿射函数”集合是KDM安全的。– 布拉克尔斯基和戈德瓦塞尔 [3]在子群不可区分性假设下展示了一种类BHHO加密方案。特别是，他们在Paillier的判定性复合剩余性 (DCR)假设下提出了一个相对于仿射函数集合的KDM安全加密方案。– 阿佩尔鲍姆等人 [2]构造了一个symmetric-key加密方案，在LPN假设下该方案相对于仿射函数集合是KDM安全的。

因此，我们可以分别在DDH假设、DCR假设和LPN假设下构造出比贝尔尔等人更高效的有界KDM安全加密方案。[6]under the DDH assumption, the DCR assumptionand the LPNassumption respectively.

我们还指出Bellare等人[6]的安全性证明并不完整，并展示了如何修复它。

2 Preliminaries

PPT 表示概率多项式时间，PT 表示多项式时间。如果A是一个概率多项式时间算法，则 y ← A(x1,…, xn; r) 表示使用输入 x1,…, xn和随机硬币 r运行算法 A以获得输出 y的操作，而y ← A(x1,…, xn) 表示随机选择 r并令 y ←A(x1,…, xn; r)。

如果 X是一个集合，则 x←$ X表示从X中随机选择 x的操作。 |X| 表示 X的基数。如果 X是一个字符串，则 |X| 表示 X的比特长度， lsb(X) 表示 X的最低有效位。如果 X和 Y是比特串，则 X‖Y表示连接。

设 k为一个安全参数。

2.1 DDH假设

设 G是一个阶为 p的素数群。DDH假设（关于 G）是指分布(g, gx, gy, gxy)与(g, gx, gy, gz)是计算上不可区分的，其中 g是 G的一个随机生成元，且 x, y, z←$ Zq。

2.2 KDM安全性

设 E=(K, E, D)为一个公钥加密方案，S={Sk}为密钥空间， M={Mk}为消息空间。对于整数 > 0,定义
ALL() k={f | f:(Sk) → Mk}。
然后，我们定义挑战者与敌手A关于函数类F={Fk}的KDM()攻击游戏，其中 Fk ⊆ ALL() k ，如下所示。

初始化。 挑战者选择 b ←${0, 1}并为所有 i ∈{1,…, }生成密钥对(ski,pki) ← K(1k)。然后挑战者将(pk1,…, pk)发送给敌手A A。

查询。 敌手A以(j, f) ∈{1,…, }×Fk的形式进行自适应查询。对于每个查询，挑战者计算 x= f(sk1,…, sk)，并将以下密文发送给敌手A A。
c={Ep k j (x) if b= 0
k j (0|x|) if b= 1

Finish. 敌手A A输出一个猜测 b′ ∈{0, 1}。

定义 Advkdm E ,(A) = |2Pr[b′= b] −1|。我们称 加密方案E 在关于 F 的意义下是 KDM() 安全的，如果 Advkdm E,对于任何PPT对手 A，(A)是可忽略的。 Th对称密钥加密方案的KDM安全性以类似方式定义 y.

2.3 BHHO加密方案

博内等人展示了在DDH假设下关于一类指数上的仿射函数的KDM安全公钥加密方案[5]。设 G为一个素数阶群 p，且 g是 G的生成元。

密钥生成。 令 t= 3 log2 p 。选择 (g1,…, gt) ←$ Gt,(s1,···, st) ←${0, 1}t。令 h ←(gs1 1 ··· gst t)−1，并将公钥和私钥定义为
pk=(g1,…, gt, h)and sk=(s1,…, st).

加密。 对于明文 m ∈ G，选择 r←$ Zp 并输出一个密文
(gr 1,…, gr t, hr · m).

解密。 对于密文 (c1,…, ct, d)，输出 m= d·(cs1 1 ··· ctst) .

我们说 f是一个指数上的仿射函数，如果 f(x1,…, xn) =ga0+∑ n i=1 aixi,，其中 xi ∈{0, 1}n且 ai ∈ Zp。以某种方式定义 Faffine={Fk}，使得
Fk= ALL() k ∩{f | f是一个指数上的仿射函数}。

命题 1[5]。 上述加密方案在DDH假设下关于 Faffine是KDM()安全的。

2.4 有界KDM安全性

设 q(k)是关于 k的一个多项式。若一个函数 f可表示为一个门数量为 q(k)的布尔电路，则称该函数为 q(k)‐有界的。定义 Fq−gates ={Fk}，其中 Fk= ALL() ∩{f | f是 q(k)‐有界的}。那么，若加密方案E相对于 Fq−gates满足KDM()安全，则称其为 q‐有界KDM()安全的加密方案。

2.5 投影 KDM安全

一个函数 f被称为 projection，如果每个输出位至多依赖一个输入位。以如下方式定义 Fp ro j ={Fk}，使得 Fk= ALL() ∩{f |f是一个投影}。我们随后称一个加密方案 E是投影KDM()安全的，如果它关于 Fp ro j 是KDM()安全的。

3 混淆方案 [6]

3.1 电路

一个布尔电路是一个五元组 f=(n, m, q, A, B, G)。其中 n ≥ 2是输入的数量， m ≥ 1是输出的数量， q ≥ 1是门数量。我们令Inputs为={1,…, n}，Gates为={n+1,…, n+ q}，Wires为={1,…, n+ q}，Outputs为={n+ q − m+ 1,…, n+ q}。那么A: Gates →Wires\Outputs 是一个用于确定每个门第一条输入线的函数，B: Gates → Wires\Outputs 是一个用于确定每个门第二条输入线的函数。我们要求对每个门 g ∈∈Gates，满足 A(g) < B(g) <g。最后，G: Gates ×{0, 1}2 →{0, 1} 是一个决定每个门功能的函数。

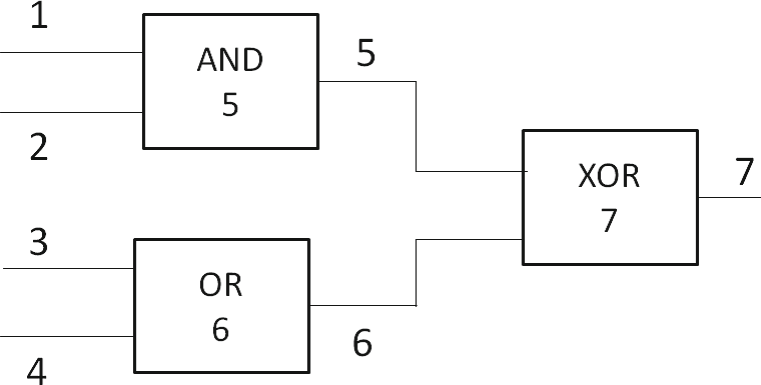
每个门有两个输入、一个输出和任意的功能。线的编号为 1 到 n+ q。输入的第 i位通过线 i给出。每个非输入线都是某个门的输出线。每个门的输出线用作该门的名称。我们用 f在输入 x ∈{0, 1}n下的输出表示为 y= f(x)。示例见附录 A。

Let Φtopo(f)=(n, m, q, A, B), Φsize(f)=(n, m, q)

我们称Φtopo(f)和 Φsize(f)为边信息函数。

3.2 混淆方案

一个混淆方案是由三个算法组成的三元组 Ga =(Gb,En,Ev)，如下所示。

– (F, e) ← Gb(1k, f)，其中 f=(n, m, q, A, B, G)是一个布尔电路， F是其混淆电路， e是加密方案E的密钥。– X ← En(e, x)，其中x ∈{0, 1}n是真实输入， X是其混淆输入。– y ← Ev(F, X)，其中 y是 F在输入 X上的输出。

正确性条件要求，如果 (F, e) ← Gb(1k, f)，那么
Ev[F, En(e, x)]= f(x) 对于任意 x ∈{0, 1}n。

3.3 混淆方案的安全性

对于混淆方案Ga =(Gb,En,Ev) 和一个侧信息函数 Φ，我们考虑挑战者与敌手 A之间进行如下游戏。

1. A选择(f0, x0)和(f1, x1)，使得 f0(x0) = f1(x1)且 Φ(f0) =Φ(f1)，并将它们发送给挑战者。2. 挑战者选择 b ←${0, 1}，并计算(F, e) ← Gb(1k, fb)和X ← En(e,xb)。然后将(F, X)发送给 A。3. A输出一个比特b′。

定义优势为 Advgarble GaΦ(A)= |2Pr(b′= b) −1|。我们说 Ga是Φ‐安全的，如果 Adv garble Ga,Φ(A)对于每个PPT对手 A都是可忽略的。 Bellare等人 [6]展示了 Φtopo‐安全的混淆方案 Ga=(Gb,En,Ev)，该方案称为 Garble1。我们在附录11和 12的图中进行了说明，参见附录 B。我们还在附录C中展示了如何构造 Φsize‐安全的混淆方案。

4 贝尔尔等人提出的有界KDM安全加密

4.1 通用构造

Bellare等人[6]基于 q‐有界KDM()安全的加密方案E′=(K′, E′, D′)构造了 – 一个Φsize‐安全的混淆方案Ga =(Gb,En, Ev) 和 – 一个投影 KDM()安全的加密方案 E=(K, E, D)。

一个在 pkj下的 f(sk1,…, sk)的密文由(F, Epkj(X))给出，其中

– F 是一个恒等电路的混淆电路 ID，且 – X 是真实输入 f(sk1,…, sk) ‖0|sk|−L, 的混淆输入，其中 L = |f(sk1,…, sk)|。

解密由以下方式给出
F(X)= ID(f(sk1,…, sk)‖0 |sk|−L)= f(sk1,…, sk)‖0 |sk|−L.

更准确地说，密钥生成算法 K′与 K相同，并输出 (pk, sk) ← K(1k)。

加密算法 E′和解密算法 D′如图1所示。存在一个电路，其门数量为 q+ n，且对于任意 z ∈{0, 1}n，有 ID(z)= z，其中 n= max(|sk| · , |x|)。

安全加密方案的通用构造。)

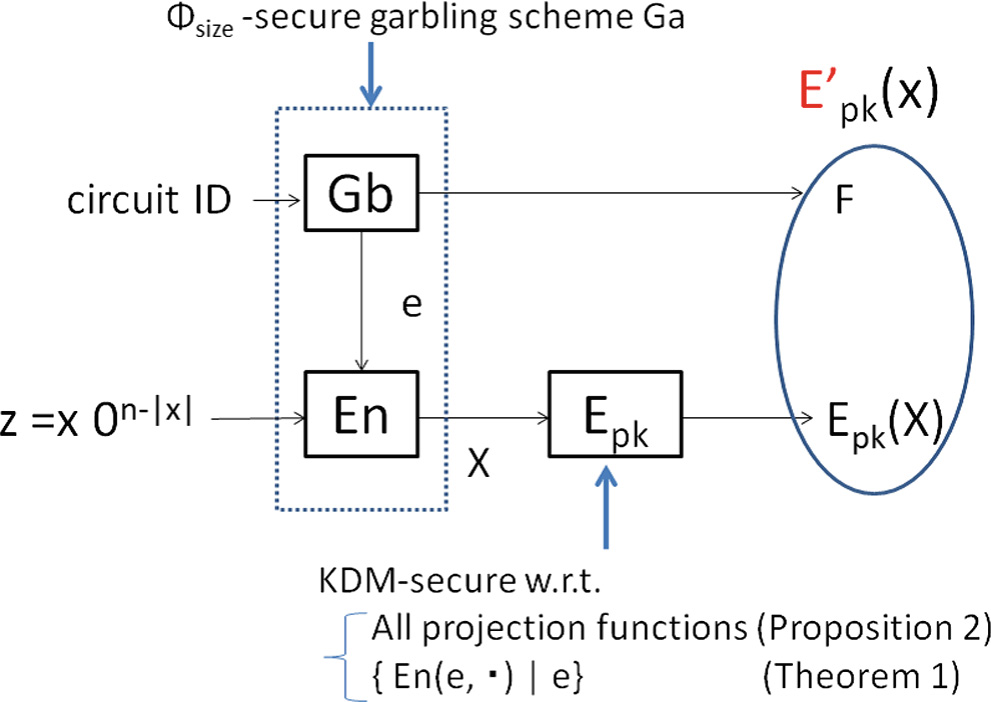
命题 2[6]。 假设

– Ga=(Gb, En, Ev)是 Φsize-安全的，且En(e,·)是一个投影函数。– E=(K, E, D)是投影KDM()安全的。

则上述加密方案 E′是 q-有界KDM()安全的。（见图2。）

。)

4.2 基于DDH的实例化

Bellare等人 [6,第7节。2]通过使用混编1[6,第 5]3和BHHO加密方案实例化命题 2 [5]。（见图3）。

安全的公钥加密方案 E′（Bellare等人）)

̂首先通过附录C中的方法，从（Φtopo‐安全的）混淆方案Garble1(Gb1, En1, Ev1) 构造一个 Φsize‐安全的混淆方案 Garble1=(Gb,En,Ev)。（参见 [6]中图 20的注释。）我们需要证明 En(e,·) 是一个投影。在 Garble1 中，

e=(X 0 1 , X 1 1 ,…, X 0 n , X 1 x 1 1 ,…, X x n

其中 Xij ∈{0, 1}k， x=（x1,…, xn）且 xi ∈{0, 1}。因此 En1（e,·）是一个投影。故 En= En1根据附录 C 的方法。

请注意
|X| = |Xx1 1 | +…+ |Xnxn | = kn. (1) 接下来，按照如下方式构造一个投影KDM()安全的加密方案 E=(K, E, D)。为了计算 Y= Epk(X)，使用BHHO加密方案对 X的每一位进行加密。具体而言，密钥生成算法 K与BHHO加密方案的密钥生成算法相同，对于 X=(ε1,…, εkn)，令
Epk(X)=(BHHOpk(gε1),…, BHHOpk(gεkn)), (2)
其中 εi ∈{0, 1} i= 1 pk gεi gεi … kn E ()
和BHHO()表示关于,,的BHHO密文。该方案在DDH假设下是投影KDM安全的。

̂得到的加密方案E′来自 Garble1以及上述 E是 q‐ 有界KDM()在 DDH假设下是安全的，依据命题2。

现在假设我们要加密 f(sk1,…, sk)。在图 1中， X= En(e, z) 在第05行的比特长度为 kn，来自公式(1)，其中
n= max(|sk| · , |f(sk1,…, sk)|) (3) 因此，第06行的Y= Epk(X)由 kn个BHHO加密方案的密文组成。整个密文包含一个混淆电路 F和 ID以及 kn个BHHO加密方案的密文。（参见[6]中图20的第三列。）

5 如何证明命题2

在本节中，我们首先指出2 Bellare等人[6]的证明并不完整。接下来，我们展示如何修复它。

5.1 贝尔尔等人提出的证明

Bellare等人 [6]证明了命题2如下。令 A为攻击E′的敌手A。为了简化阐述，他们首先考虑 A仅进行一次查询的情况。然后，他们简要说明如何将其推广到一般情况。

Single query case。 假设 A提出一个查询（j, f）。设 C是一个具有 n条输入线、 n条输出线和 q+ n个门的电路，使得
C(x)= f(the first |sk| bits of x)‖0 n−|f(sk1,···,sk )|,
其中 n= max(|sk| · , |f(sk1,…, sk)|)。然后我们有
C(K)= f(sk1‖···‖sk)‖0 n−|f(sk1 ,···,sk ) | (4)
对于K= sk1‖···‖sk‖0 n−|sk|·。

我们考虑一系列博弈 G0，......， G4，如图4所示，其中 G0等价于使用 b= 0的KDM攻击游戏，因为 C（K）由公式（4）给出。每一场博弈逐步修改图1中的第04–05行。令 pi=为博弈 Gi中输出1的概率。

– |p0 −p1| 是可忽略的，因为ID(C(K)) = C(K)， Φsize(ID) = Φsize(C)，且混淆方案是 Φsize‐安全的。 – |p1−p2| 是可忽略的，因为En(e,·)是一个投影函数，且 E关于{所有投影函数}是KDM()安全的。 – p2= p3因为在每一轮游戏中(F, Epkj(X))都相同。 – |p3 −p4| 是可忽略的，因为ID(C(0n)) = C(0n)， Φsize(ID) =Φsize(C)，且混淆方案是 Φsize‐安全的。

他们的证明在此处停止。然而，GameG4并不是关于 b= 1的KDM攻击游戏。

5.2 如何修正证明

为了完成该证明，我们使用以下命题。

命题 3[5]。 假设函数类 F包含所有常数函数。那么关于 F的KDM安全性意味着 IND-CPA安全性。

任何常数函数都是投影函数。因此，所有投影函数的集合包含所有常数函数。

现在我们添加游戏 G5和游戏 G6，如图5所示。然后

– p4= p5因为(F, E p k j (0|X|)) 在每个游戏中都相同。– |p5 −p6| 是可忽略的，因为 E是 IND‐CPA安全 的，根据命题 3。

游戏 G6 是带有 b= 1 的 KDM 攻击游戏，因为游戏 G6 的输出是 E′ p k j (0|f(sk1‖···‖sk) |)。最后，根据上述讨论， |p0 −p6| 可忽略。这完成了证明。

6 我们的主要定理

如上所述，有界KDM安全性可以从投影KDM安全性获得。然而，密文大小仍然非常大。在本节中，我们展示它可以从比投影KDM安全性弱得多的概念中获得。

加密方案 E′=(K′, E′, D′) 如图1所示，由以下部分组成

– 一个混淆方案Ga =(Gb,En,Ev) 和 – 一个加密方案 E=(K, E, D)，使得K′= K。

我们用 E′(Ga E) 表示这样的E′。

对于混淆方案Ga =(Gb,En,Ev)，首先定义En为
̂Enn,e(x)= En(e, x‖0n−|x|). (5)

接下来定义函数集 F(Ga) ={Fk} 如下。
Fk= ALL() k ∩{̂Enn,e | (F, e) ← Gb(1k, C), where Φsize(C)=(n, n, n+ q)}.

那么我们的主定理如下。（见图2。）

定理1。 E′(Ga E)是 q-有界KDM()安全的，如果Ga是 Φsize-安全的，并且 E是 IND-CPA安全的且关于 F(Ga)是KDM()-安全的。

The 证明与命题的证明相同2我们已对此进行了修正。特别是 r,

– |p1 −p2| 可忽略，因为 E相对于 F(Ga)是KDM()安全的。– |p5 −p6| 可忽略，因为 E是IND‐CPA安全的。

̂令 Ga表示通过附录C中的方法从一个Φtopo‐安全的混淆方案 Ga得到的 Φsize‐安全混淆方案。那么我们有以下推论。

推论1. E′(̂Ga E)是 q-有界KDM()安全的，如果 Ga是 Φtopo-安全的，并且 E是IND-CPA安全的且关于 F(Ga)是KDM()安全的。

̂证明.设 Ga=(Gb′,En′,Ev′) 且 Ga=(Gb, En, Ev)。那么 En′= En按照附录C中的方法。因此我们由F(Ga) 的定义得到该推论。

让我们比较定理 1与命题2。

– 在命题2中， E需要关于“所有投影函数”集合是KDM()安全的。因此 Bellare等人不得不使用BHHO加密方案对 X= En(e, z) 的每一位进行加密。– 而在我们的定理中， E只需要关于 F(Ga) 是 KDM()安全的。因此我们可以构造一个更高效的 E，通过在后续章节中展示的适当混淆方案 Ga来实现。

另一个区别是，在定理1中， E需要是IND‐CPA安全的。然而，这并不是问题，因为任何加密方案本身就必须是IND‐CPA安全的。参见表1。

方案	Ga的En	E必须关于KDM安全
BHR [6]	所有投影函数的集合 投影
本文提出	(Ga)	−−
## 7 基于DDH的实例化
在本节中，我们展示了一种比Bellare等人更高效的有界KDM安全加密方案̂E′(Ga E)，该方案基于推论1并在DDH假设下成立。该加密方案 E基于BHHO加密方案[5], ，且混淆方案Ga是Garble的一个变体1[6]，我们称之为Garble1+。

设 G为一个素数阶群， g是 G的生成元，如BHHO加密方案所要求。

7.1 混淆1+

我们定义Gb、Ev为如图6和图7所示的Garble1+中的内容。即
e=(u01, u11,…, u0n, u1n), (6)
En(e, x)=(gu x1 1,…, gu xn
n), (7)
其中 uj i ∈ Zp，以及
X0 i ← H(g u0
i), X 1 i ← H(g u1
i) (8)
对于Gb中的 i= 1,…, n，其中 H: G →{0, 1}k是一个哈希函数，使得当
v ←$ G时， H(v)在{0, 1}k上均匀分布。

其余部分与Garble相同1[6]如附录B所示。然后Garble1+是 Φtopo‐安全的，类似于Garble1。

。)

。)

7.2 关于 F(Garble1+) 的KDM安全加密

接下来我们展示一个高效的加密方案 E=(K, E, D)，该方案关于 F(Garble1+) 是 KDM()‐安全的。

– 密钥生成算法 K 与 BHHO加密方案 的密钥生成算法相同。令 (sk,pk) ← K(1k)。– 对于消息 (m1,…, mn) ∈ G n，令
Epk(m1,…, mn)=(BHHOpk(m1),…, BHHOpk(mn)). (9)
我们强调，在上述加密方案中mi ∈ Gn，而 mi ∈{1, g}在Bellare等人提出的方案中[6]。

定理2. 上述加密方案 E=(K, E, D)在DDH假设下是IND-CPA安全的，并且关于 F(Garble1+)是KDM()安全的。

证明。 E是IND‐CPA安全的，因为BHHO加密方案是IND‐CPA安全的。我们将证明它关于 F(Garble1+)是KDM()安全的。

在KDM()攻击游戏中，挑战者为所有 i ∈{1,…, }生成密钥对(ski,pki) ←K(1k)。
定义 L= |sk| 并令
(sk1,…, sk)=(s1,…, sL),
其中 si ∈{0, 1} 对于 i= 1,…, L。

那么对于 e=(u01, u 1
̂Enn,e(sk1,…, sk)= ̂Enn,e(s1,…, sL)
=(g u
s 1
1,…, g u
s L
L, g u 0
L+1,…, g u 0
n)
由公式(7)和(5)可得。进一步由公式(9)，我们有
E pk(̂Enn,e(sk1,…, sk))= E pk(g u
s 1
1,…, g u
s L
L, g u 0
L +1,…, g u 0
n)
=(BHHOp k(g u
s 1 1),…, BHHOp k(g u
s L
L),
BHHO p k(g u 0
L +1),…, BHHOp k(g u 0
n)).

我们注意到
u0i+(u1i − u0i)× si={u0i if si= 0 u1i if si= 1
因此我们有
usi i= u0i+(u1i − u0i)× si.
这意味着对于固定的 e=(u01, u 1 i是(s1,…, sL)的仿射函数。更准确地说，令 a0= u0i和
aj={u1i − u0i if j= i otherwise
然后 usi i被写成
usi i= a0+
L
∑
j=1
aj sj.
Let
Expe(s1,…, sL)i= gu si i= ga0+∑ L j=1 aj sj. (10)
然后 Expe(s1,…, sL)i属于第 Faffine节 2.3中的 i= 1,…, L。此外，对于i= L+ 1,…, n， gu 0 i是常数函数，因此它们也属于 Faffine。

设 A为一个针对 E关于 F(Garble1+)的敌手A。我们构造一个敌手B，用于攻击 BHHO加密方案关于 Faffine，具体如下。
收到挑战者发送的(pk1,…, pk)后， B将它们发送给 A。假设 A查询(j,̂
Enn,e)，使得 e=(u01, u 1
1. 对于 i= 1，…， L， B查询（j，Expe（·）i）发送给挑战者，并收到一个密文 ci，其中Expe（·）i由公式(10)定义。 2. 对于 i= L+ 1，…， n， B查询（j，g u 0 i）发送给挑战者，并收到一个密文 ci。 3. B将 C=（c1，…， cn）返回给 A。
̂容易看出， C是(j,Enn,e)的一个正确的挑战密文。最后， B输出 A所输出的任何内容。因此，在DDH假设下，Advkdm E ,(A) =Adv kdm BHHO,(B)在 DDH假设下是可忽略的。

7.3 最终构造

最后，我们的 q‐有界KDM()‐安全的加密方案 E′是通过将Garble1+和第7.2节中的加密方案 E代入推论1（图8）得到的。

推论2。 设 E为第7.2节给出的加密方案。则在DDH假设下，E′（ ̂ Garble1+, E）是 q-有界KDM()-安全的。

证明。 由推论 1和定理2得出。

安全的公钥加密方案 E′。)

8 比较

让我们比较两种 q‐有界KDM()‐安全的加密方案在DDH假设下的表现（即第4.2节和7节中的方案）。在这两个方案中，E′ pk(x1,…, xn) 由 (F, Y) 组成，其中 F是 ID的混淆电路。我们比较表 2 和 3中的 {v44}。

方案	E=(K, E, D)	X
敌手B [6]	投影KDM安全	(Xx1 1,…, Xxn n)，其中 Xxi i$←{0, 1}k
本文提出	F(Garble1+)‐KDM安全	(gu

方案	Y= Epk(X)
敌手B [6] 提出的BH	对 Xxi i ∈{0, 1}k的每一位使用BHHO加密，得到 i= 1,…, n HO加密 g x
	u i

我们的 E仅关于 F(Garble1+)是KDM安全的，而在Bellare等人的方案中，它必须关于所有投影函数的集合是KDM安全的。因此

– Epk( X) 在我们的方案中对 g u
x i
的方案中，必须对 Xx i
i ∈{0, 1}k 的每一位分别进行加密，以用于 i= 1,…, n
BHHO加密方案的每个密文大小为 O(k2)，来自第2.3节，其中 log p= O(k)。
因此 – 在我们的方案中为 |Y | = O(k2n)，在 Bellare等人的方案中为 |Y | = O(k3n)
因此在我们的方案中， |Y | 被简化为 1/k。

电路 ID的门大小为 r= q+ n，来自图 1 的第101–105 行。因此，实现 ID的通用电路具有门大小 O(r log r)，见公式(12)。因此，在两个方案中， |F| = O(kr log r)，因为 F的每个门的大小为 O(k)。密文的总大小 |F| + |Y | 见表 4 。

方案	混淆电路 F Y=	Epk(X) 总大小
敌手B HR [6]	O(kr log r)	O(k3n)	O(kr log r) + O(k3n)
本文提出	O(kr log r)	O(k2n)	O(kr log r) + O(k2n)

当加密 f(sk1,…, sk) 时， n= max(|sk| · , |f(sk1,…, sk)|)。假设 |f(sk1,…, sk|) = O(|sk| · ) 且 q= O(n)。则 n= O(|sk| · )=O(k) 且 r= q+ n= O(n) = O(k)。
在这种情况下， O(k2n) = O(k3)， O(k3n) = O(k4) 且 O(kr log r) = O(k2log k)，因为 n= poly(k)。因此，在我们的方案中密文的总大小为 O(k3)，而在 Bellare 等人的方案中为 O(k4)。因此，我们的方案小了 k 倍（表5）。

方案	混淆电路 F Y=	Epk(X) 总大小
BHR [6]	O(k2log k)	O(k4)	O(k4)
本文提出	O(k2log k)	O(k3)	O(k3)

9 推广

通常情况下，我们可以构造 – 一种关于 F(Garble1)的KDM安全加密方案，来自任意关于仿射函数集合的 KDM安全加密方案，以及 – 一种关于 F(Garble1+)的KDM安全加密方案，来自任意关于指数上的仿射函数集合的KDM安全加密方案，
其中密钥被视为一个比特串。通过使用其中每一项，我们可以基于推论1构造一个有界 KDM安全加密方案。

如果我们的弱KDM安全加密方案的消息空间足够大，那么我们的 Y的大小比Bellare等人[6]小 k倍。在本节中，我们展示此类示例。

9.1 对称密钥加密方案

命题2对于对称密钥加密方案也成立，如[6]中所述。类似地，我们的定理1和 推论1也适用于对称密钥加密方案。证明过程相同。

阿佩尔鲍姆等人 [2]提出了一个 symmetric-key 加密方案E，该方案相对于仿射函数集合（不在指数上）是KDM()安全的，其安全性基于
LPN假设。我们称之为ACPS加密方案。我们可以在LPN假设下构造一个有界 KDM()安全的symmetric-key加密方案，具体如下。我们使用Garble1。然后
e=(X0 1, X1 1,…, X0 n, X1 n), X= En(e, x)=(Xx1 1,…, Xnxn),
其中 Xj i ∈{0, 1}k， x=（x1,…, xn）且 xi ∈{0, 1}。为计算图1的第06行中的 Y= Epk（X），使用ACPS加密方案对每个 Xj i进行加密。即
E(X)=(ACPS(Xx1 1),…, ACPS(Xnxn)),
其中 ACPS(Xxi i) 表示 Xxi i 的 ACPS 密文。现在 Xxi i 被写作
Xxi i= X0 i+(X1 i − X 0 i)× xi. (11)
这意味着 Xxi i是(x1,…, xn)的仿射函数。因此我们可以证明 E关于 F（Garble1）是KDM()安全的。因此，在推论1（图9）的LPN假设下， E′（ ̂ Garble1, E）是 q‐有界KDM()安全的。
另一方面，如果我们使用命题2，则必须使用ACPS加密方案对每个比特进行 Xj i加密。

安全的对称密钥加密方案 E′。)

9.2 子群不可区分性假设

布拉克尔斯基和戈德瓦塞尔[3]在子群不可区分性假设下展示了一种类BHHO 加密方案。特别地，他们在Paillier的判定性复合剩余性(DCR)假设下提出了一 个关于仿射函数集合的KDM安全加密方案。在此加密方案中，消息空间为ZN， 其中 N= pq。

现在，我们可以通过将我们的技术应用于该加密方案和Garble1，在 DCR假设下构建一个有界KDM()安全的公钥加密方案。