Codeforces Round #747(Div.2)

A - Consecutive Sum Riddle

题意：给定一个整数 ，求一个区间满足：

思路：

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
    ll t,n;
    cin>>t;
    while(t--)
    {
        cin>>n;
        //l*(r-l)+(r-l)*(r-l-1)/2==n
        cout<<-(n-1)<<" "<<n<<endl;
    }
}

B - Special Numbers

题意：

 对于给定的n（n是某个数的幂底），幂底数的累加和形成一个递增序列，求第K个数是什么？

例：当n=3,k=4时，递增序列为：{1，3，4，9，10，12，27........},答案是9。

思路：

二进制转换成十进制：         

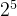
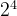
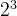
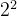
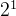
                                   1    0    1    1    0    1

                       

本题：十进制转换成二进制，不过权值是n的幂，不是2的幂啦！

                                             

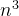
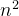
                                    1       0      1     1 

                       

                  下图第一列是递增序列顺序排列：

					K
	0	0	0	1	1
	0	0	1	0	2
	0	0	1	1	3
	0	1	0	0	4
	0	1	0	1	5
	0	1	1	0	6
	0	1	1	1	7
	1	0	0	0	8
	1	0	0	1	9
	1	0	1	0	10
	1	0	1	1	11
	1	1	0	0	12
	1	1	0	1	13
	1	1	1	0	14
	1	1	1	1	15

给你一个K，将它转换成二进制形式，那么我们就知道谁是0，谁是1。将其按照n的幂的权转换成十进制。

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod =1e9+7;
int main()
{
	int t;
    ll n,k;
	cin>>t;
	while(t--)
    {
		vector<int>a;
		ll ans=0;
		cin>>n>>k;
        while(k)
        {
            a.push_back(k%2);
            k/=2;
        }
        ll x=1;
        for(int i=0;i<a.size();i++)
        {
            //(n,i)

            if(a[i]==1)
            {
                ans=(ans+x)%mod;
            }
            x=x*n%mod;
        }
        cout<<ans<<endl;
	}
	return 0;
}

C - Make Them Equal

题意：给你一个字符串和一个字符，进行最少的操作使 中每个字符等于。

操作：选择一个数字，对于每个位置，只要不能被整除，用替换。

 输出最小的操作数及选择的。

样例解释：

4 b
bzyx

2 
2 3

思路：

三种情况：当S中的每个字符都等于C，则不需要操作；在1~n内选一个除数，那么肯定是越大越好。比如选x，显然比x小的数是不可能整除x的，所以1到n-1内的数就全被变成C了.然后最多再选一个不是x的因子的数就能把第n个数变成C了。因此，最多选两个数即可完成要求(n和n-1肯定互质).

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod =1e9+7;
const int maxx=3e5+10;
char s[maxx];
int main()
{
	int t,n;
	char c;
	cin>>t;
    while(t--)
    {
        cin>>n>>c;
        scanf("%s",s+1);
        bool f=true;
        for(int i=1;i<=n;i++)
        {
            if(s[i]!=c)
            {
                f=false;
                break;
            }
        }
        if(f)
        {
            cout<<"0"<<endl;
            continue;
        }

        for(int i=1;i<=n;i++)
        {
            f=true;
            for(int j=i;j<=n;j+=i)
            {
                if(s[j]!=c)
                {
                    f=false;
                    break;
                }
            }
            if(f==true)
            {
                cout<<"1"<<endl<<i<<endl;
                break;
            }
        }
        if(f==false)
        {
            cout<<"2"<<endl;
            cout<<n-1<<" "<<n<<endl;
        }
    }
	return 0;
}