数据结构_Chapter2.3.3 函数与递归

浙大陈越老师主编《数据结构》（第2版）学习笔记

目录

汉诺塔（Tower of Hanoi）问题

求集合的中位数

---

汉诺塔（Tower of Hanoi）问题

传说印度的主神梵天做了一个汉诺塔，它是在一个黄色铜板上插3根宝石针，其中一根针上从上到下按从小到大的顺序串上了64个金片。梵天要求僧侣们轮流把金片在3根针之间移来移去，规定每次只能移动一片，且不许将大金片压在小金片上，并说如果这64片金片全部移至另一根针上时，世界就会在一声霹雳之中毁灭。

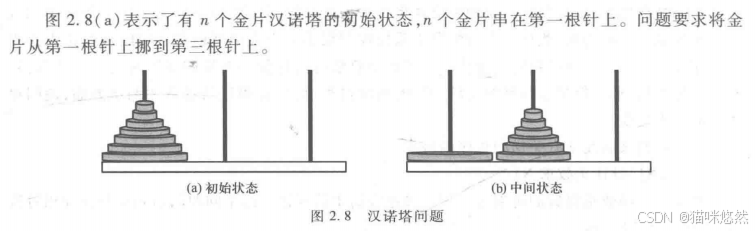
从递归的角度考虑，问题将变简单。

要想将这n片金片从第一根针移动到第三根针，一定会移成图2.8(b)所示的情况，即第一根针(起始针)上只剩第n片金片，其余n-1片移动到第二根针(过渡针)。

那么将n片金片从第一根针移动到第三根针这个问题就分解成了3步：

1. 将上面的n-1片金片从第一根针(起始针)移动到第二根针(过渡针)
2. 将下面的第n片金片从第一根针(起始针)移动到第三根针(目标针)
3. 将n-1片金片从第二根针(过渡针)移动到第三根针(目标针)

上面的步骤1和3还需要继续分解，直到完成整个移动为止。

我们来尝试继续分解步骤1（将n-1片金片从第一根针移动到第二根针），可以分解成与上面相似的3步：

1. 将上面的n-2片金片从第一根针(起始针)移动到第三根针(过渡针)
2. 将下面的第n-1片金片从第一根针(起始针)移动到第二根针(目标针)
3. 将n-2片金片从第三根针(过渡针)移动到第二根针(目标针)

同样的，上面的步骤1和3还需要继续分解。

根据上面的分析，拟设计递归函数Move如下：

void Move(int n, int start, int goal,int temp)

其中n代表金片个数，start为起始针，goal为目标针，temp为过渡针

Move(n, start, goal, temp)分解为：

1. Move(n - 1, start,  temp, goal)
2. 将第n片从start移动到goal
3. Move(n - 1, temp, goal, start)

代码如下：

/* 汉诺塔问题 */
void Move(int n, int start, int goal, int temp)
{
    if(0 == n)
    {
        return;
    }

    Move(n -1, start, temp, goal);
    printf("Move disk %d tower %d -> %d \n", n, start, goal);
    Move(n - 1, temp, goal, start);
    return;
}

int main()
{
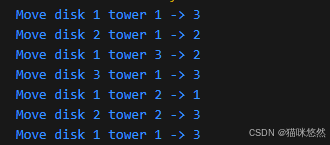
    Move(3, 1, 3, 2);
}

将n设为3时，运行结果如下：

求集合的中位数

这个问题可以建立在求集合第k大元素问题上，当k等于集合大小的一半时，第k大元素就是中位数。

基本思路是：选取集合中的一个元素作为基准e，将集合分为大于等于e的元素集合S1、|e|、小于e的元素集合S2，通过判断S1的大小，将问题转换为在S1或S2中的查找第k大元素的问题。

思路：

1. 以集合最左边元素为基准e；
2. 从左往右扫描，发现小于e的元素，暂停；
3. 从右往左扫描，发现比大于/等于e的元素，暂停；
4. 此时，若左右两个暂停点还未相会，则交换两个元素；
5. 重复以上步骤，直至左右两个暂停点在中间某处相会，相会的位置即基准e把两个集合S1、S2分开的位置，将基准e交换到这个位置。
6. 集合S1的元素个数等于k-1，则e即为第k大元素；集合S1的元素个数大于等于k，则在S1中找第k大元素，否则，在S2中找。

代码如下：

#include <stdio.h>
#include <stdlib.h>

void swap(int* x, int* y)
{
    int temp;

    temp = *x;
    *x = *y;
    *y = temp;
}

int find_k_th_largerst(int* array, int k, int left, int right)
{
    /* 在array中找第k大的元素 */
    int i;
    int e = array[left];  /* 以e为基准 */
    int l_side = left;
    int r = right;

    printf("k:%d, left:%d right:%d \n", k, left, right);

    /* 将array中比e大的移到左边，小的移到右边 */
    while(1)
    {
        /* 从左往右扫描，找到比e小的数，停止 */
        while(l_side <= r && array[l_side] >= e)
        {
            l_side++;
        }
        /* 从右往左扫描，找到比e大或相等的数，停止 */
        while(l_side < r && array[r] < e)
        {
            r--;
        }

        if(l_side < r)
        {
            printf("swap array[%d](%d) array[%d](%d) \n", l_side, array[l_side], r, array[r]);
            swap(&array[l_side], &array[r]);
        }
        else
        {
            break;
        }
    }

    printf("left[%d] right[%d] \n", l_side, r);

    /* l_side - 1处为大于等于e的集合的最后一个元素，将e换到此处 */
    swap(&array[l_side -1], &array[left]);
    for(i = left; i <= right; i++)
    {
        printf("%d ", array[i]);
    }
    printf("\n");

    /* 判断index为（l - 1）的元素是否为第k个元素 */
    if((l_side - 1 - left) == (k -1))
    {
        return e;
    }
    else if((l_side - 1 - left) > (k -1))
    {
        /* 在左侧集合里找 */
        return find_k_th_largerst(array, k, left, l_side -2);
    }

    /* 在右侧集合里找(index为l的元素左侧有（l_side - left）个元素) */
     return find_k_th_largerst(array, k - (l_side - left), l_side, right);
}

int median(int* array, int n)
{
    int ret = find_k_th_largerst(array, (n + 1) / 2, 0, n -1);
    printf("median number is %d \n", ret);
    return ret;
}

int main()
{
    int array[6] = {1, 2, 3, 4, 5, 6};

    median(array, sizeof(array) / sizeof(array[0]));
    return 0;
}

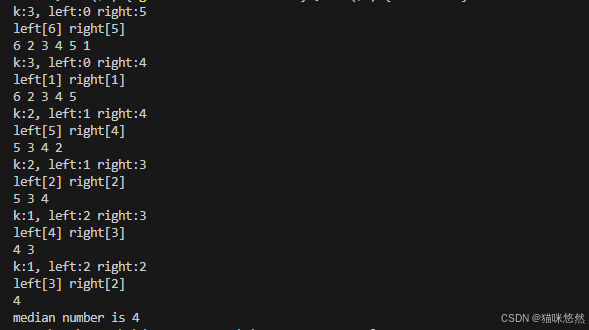
运行结果：