Cracking the Coding Interview 150题（二）-CSDN博客

3、栈与队列

3.1 描述如何只用一个数组来实现三个栈。

3.2 请设计一个栈，除pop与push方法，还支持min方法，可返回栈元素中的最小值。pop、push和min三个方法的时间复杂度必须为O(1)。

3.3 设想有一堆盘子，堆太高可能会倒下来。因此，在现实生活中，盘子堆到一定高度时，我们就会另外堆一堆盘子。请实现数据结构SetOfStacks，模拟这种行为。SetOfStacks应该由多个栈组成，并且在前一个栈填满时新建一个栈。此外，SetOfStacks.push()和SetOfStacks.pop()应该与普通栈的操作方法相同（也就是说，pop()返回的值，应该跟只有一个栈时的情况一样）

进阶：实现一个popAt(int index)方法，根据指定的子栈，执行 pop 操作。

3.4 在经典问题汉诺塔中，有3根柱子及N个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自底向上从大到小依次套在第一根柱子上（即每一个盘子只能放在更大的盘子上面）。移动圆盘时有以下限制：

每次只能移动一个盘子
盘子只能从柱子顶端滑出移到下一根柱子
盘子只能叠在比它大的盘子上

请运用栈，编写程序将所有盘子从第一根柱子移到最后一根柱子。

3.5 实现一个MyQueue类，该类用两个栈来实现一个队列。

3.6 编写程序，按升序对栈进行排序（即最大元素位于栈顶）。最多只能使用一个额外的栈存放临时数据，但不得将元素复制到别的数据结构中（如数组）。该栈支持如下操作：push、pop、peek和isEmpty。

3.7 有家动物收容所只收容狗与猫，且严格遵守“先进先出”的原则。在收养该收容所的动物时，收养人只能收养所有动物中“最老”（根据进入收容所的时间长短）的动物，或者，可以挑选猫或狗（同时必须收养此类动物中“最老”的）。换言之，收养人不能自由挑选想收养的对象。请创建适用于这个系统的数据结构，实现各种操作方法，比如enqueue、dequeueAny、dequeueDog和dequeueCat等。

4、树与图

4.1 实现一个函数，检查二叉树是否平衡。在这个问题中，平衡树的定义如下：任意一个结点，其两棵子树的高度差不超过1。

4.2 给定有向图，设计一个算法，找出两个结点之间是否存在一条路径。

4.3 给定一个有序整数数组，元素各不相同且按升序排列，编写一个算法，创建一棵高度最小的二叉查找树。

4.4 给定一棵二叉树，设计一个算法，创建含有某一深度上所有结点的链表（比如，若一棵树的深度为D，则会创建出D个链表）。

4.5 实现一个函数，检查一棵二叉树是否为二叉查找树。

4.6 设计一个算法，找出二叉查找树中指定结点的“下一个”结点（即中序后继）。可以假定每个结点都含有指向父结点的连接。

4.7 设计并实现一个算法，找出二叉树中某两个结点的第一个共同祖先。不得将额外的结点储存在另外的数据结构中。注意：这不一定是二叉查找树。

4.8 你有两棵非常大的二叉树：T1，有几百万个结点；T2，有几百个结点。设计一个算法，判断T2是否为T1的子树。（如果T1有这么一个结点n，其子树与T2一模一样，则T2为T1的子树。也就是说，从结点n处把树砍断，得到的树与T2完全相同。）

4.9 给定一棵二叉树，其中每个结点都含有一个数值。设计一个算法，打印结点数值总和等于某个给定值的所有路径。注意，路径不一定非得从二叉树的根结点或叶结点开始或结束。

参考答案（C++）

3.1 描述如何只用一个数组来实现三个栈。

这个问题的难易程度取决于每个栈是固定分割 还是 动态分割。

固定分割：也就是每个栈分配固定大小的空间。这是最简单的实现方法，但是效率不高，因为即使某个栈是空的，它的空间也不能被别的栈使用。下面是每个栈占数组1/3的实现代码：

class Stacks
{
private:
    static const int size = 100;  // 每个栈的大小
    int tops[3];                  // 3个栈的栈顶指针
    int arr[3*size];              // 共享的数组
    int absTopOfStack(int flag);  // 返回栈顶指针在数组中的绝对量
public:
    Stacks();
    bool isEmpty(int flag);  // flag用0,1,2分别表示对3个栈进行操作
    void push(int value, int flag);
    int pop(int flag);
    int top(int flag);
};

Stacks::Stacks()
{
    for(int i=0; i<3; ++i)
        tops[i] = -1;
}

int Stacks::absTopOfStack(int flag)
{
    return flag * size + tops[flag];
}

bool Stacks::isEmpty(int flag)
{
    return tops[flag] == -1;
}

void Stacks::push(int value, int flag)
{
    if(tops[flag]+1 >= size) /*检查有无空闲空间*/
    {
        std::cout << "Out of space.\n";
    }
    else
    {
        ++tops[flag];
        arr[absTopOfStack(flag)] = value;
    }
}

int Stacks::pop(int flag)
{
    if(isEmpty(flag))
    {
        std::cout << "Trying to pop an empty stack.\n";
        exit(1);
    }
    int value = arr[absTopOfStack(flag)];
    arr[absTopOfStack(flag)] = 0;   /*清零*/
    --tops[flag];  /*指针自减*/
    return value;
}

int Stacks::top(int flag)
{
    return arr[absTopOfStack(flag)];
}

动态分割：允许栈的大小灵活可变，要实现起来难度有点大。
- 思路一：我们可以先考虑用一个数组实现两个栈，思路很简单：分别用数组的两端作为两个栈的起点，向中间扩展，若两个栈中的元素总和不超过n，两个栈不会重叠。基于同样的想法，我们可以把第三个栈实现在数组的中部，当前两个栈中有一个满了（即将重叠第三个栈时），平移第三个栈以扩展栈空间。这种方法由于需要搬移元素所以效率不高。
- 思路二：链式栈。通过链表的方式来实现栈，如下图：

链式栈是在一个数组上实现多个栈（3个、4个、5个…）的通用解决方案。下面是示例代码：

struct Node
{
    int key;       // 存储关键字
    int preIndex;  // 记录上一个元素的位置
};

class Stacks
{
private:
    int top1, top2, top3;
    int array_size;  // 数组的大小，即栈的最大容量
    int current_ptr; // 下一个元素入栈的位置
    Node* arr;
public:
    Stacks(int size);
    ~Stacks();
    bool isEmpty(int flag);  // flag用0,1,2分别表示对3个栈进行操作
    void push(int value, int flag);
    int pop(int flag);
    int top(int flag);
};

Stacks::Stacks(int size):array_size(size),
    top1(-1),top2(-1),top3(-1),current_ptr(0)
{
    arr = new Node[size];
}

Stacks::~Stacks()
{
    delete [] arr;
}

bool Stacks::isEmpty(int flag)
{
    switch(flag)
    {
    case 0:
        return top1 == -1;
    case 1:
        return top2 == -1;
    case 2:
        return top3 == -1;
    default:
        cout << "Error flag of stack.\n";
        exit(1);
    }
}

void Stacks::push(int value, int flag)
{
    if(current_ptr == array_size) // 栈已满
    {
        cout << "Stack is full.\n";
        return;
    }
    else
    {
        arr[current_ptr].key = value;
        switch (flag)
        {
        case 0:
            arr[current_ptr].preIndex = top1;
            top1 = current_ptr;
            break;
        case 1:
            arr[current_ptr].preIndex = top2;
            top2 = current_ptr;
            break;
        case 2:
            arr[current_ptr].preIndex = top3;
            top3 = current_ptr;
            break;
        default:
            break;
        }
        ++current_ptr;
    }
}

int Stacks::pop(int flag)
{
    if(isEmpty(flag))
    {
        cout << "Trying to pop an empty stack.\n";
        exit(1);
    }
    int value;
    switch (flag)
    {
    case 0:
        value = arr[top1].key;
        top1 = arr[top1].preIndex;
        break;
    case 1:
        value = arr[top2].key;
        top2 = arr[top2].preIndex;
        break;
    case 2:
        value = arr[top3].key;
        top3 = arr[top3].preIndex;
        break;
    default:
        break;
    }
    return value;
}

int Stacks::top(int flag)
{
    switch (flag)
    {
    case 0:
        return arr[top1].key;
    case 1:
        return arr[top2].key;
    case 2:
        return arr[top3].key;
    default:
        break;
    }
}

3.2 请设计一个栈，除pop与push方法，还支持min方法，可返回栈元素中的最小值。pop、push和min三个方法的时间复杂度必须为O(1)。

通常来说pop和push方法的时间复杂度就是O(1)，关键是min方法。

可能有人会想在Stack类里添加一个int型的变量用来记录最小值。当新元素入栈时，比较新元素与最小值，若新元素更小则更新最小值，此时push的时间效率是O(1)；但是当 minValue 出栈时，我们需要遍历整个栈，找出新的最小值，此时pop操作的时间效率就不符合O(1)的要求了。

思路一：记录每种状态下的最小值。通过给栈元素增加一个 min 字段，每个元素在入栈时记录当前状态下的最小值。这么一来，要找到最小值，直接查看栈顶元素的 min 就行了。

struct node {
    int value;
    int min;
};

class Stack {
private:
    std::stack<node> s;
public:
    void push(int v);
    int pop();
    int min();
};

/**********实现***********/
void Stack::push(int v)
{
    node n;
    n.value = v;
    n.min = v < min() ? v : min();
    s.push(n);
}

int Stack::pop()
{
    if(s.empty())
    {
        std::cout << "Trying to pop an empty stack.\n";
        exit(1);
    }

    int top = s.top().value;
    s.pop();
    return top;

}

int Stack::min()
{
    if(s.empty())
        return INT_MAX;
    else
        return s.top().min;
}

思路二：利用辅助栈保存最小值。这种方法比思路一更节省空间一些 ———— 因为思路一中每个栈元素都要记录 min，而使用辅助栈，当入栈元素大于当前最小值时，不需要记录。

class Stack {
private:
    std::stack<int> s;
    std::stack<int> min_s;  // 辅助栈
public:
    void push(int v);
    int pop();
    int min();
};

/**********实现***********/
void Stack::push(int v)
{
    if(v <= min())
        min_s.push(v);
    s.push(v);
}

int Stack::pop()
{
    if(s.empty())
    {
        std::cout << "Trying to pop an empty stack.\n";
        exit(1);
    }
    int top = s.top();
    s.pop();
    if(top == min())
        min_s.pop();

    return top;
}

int Stack::min()
{
    if(min_s.empty())
        return INT_MAX;
    else
        return min_s.top();
}

3.3 设想有一堆盘子，堆太高可能会倒下来。因此，在现实生活中，盘子堆到一定高度时，我们就会另外堆一堆盘子。请实现数据结构SetOfStacks，模拟这种行为。SetOfStacks应该由多个栈组成，并且在前一个栈填满时新建一个栈。此外，SetOfStacks.push() 和 SetOfStacks.pop() 应该与普通栈的操作方法相同（也就是说，pop() 返回的值，应该跟只有一个栈时的情况一样）

根据题意，SetOfStacks中应该有一个栈数组，而push和pop都是操作栈数组中的最后一个栈。入栈时若最后一个栈被填满，就需新建一个栈；出栈后若最后一个栈为空，就必须从栈数组中移除这个栈。

class SetOfStacks
{
private:
    vector<stack<int>> stacks;
    int capacity;  // 一个栈的最大存储量
public:
    SetOfStacks(int cap);
    void push(int v);
    int pop();
};

/**********实现**********/
SetOfStacks::SetOfStacks(int cap)
{
    this->capacity = cap;
}

void SetOfStacks::push(int v)
{
    if(!stacks.empty() && stacks.back().size() < capacity)
    {
        stacks.back().push(v);
    }
    else
    {
        stack<int> s;  // 必须新建一个栈
        s.push(v);
        stacks.push_back(s);
    }
}

int SetOfStacks::pop()
{
    if(stacks.empty())
    {
        cout << "Trying to pop an empty stack.\n";
        exit(1);
    }
    int value = stacks.back().top();
    stacks.back().pop();
    if(stacks.back().empty())
        stacks.pop_back();  // 移除
    return value;
}

进阶：实现一个popAt(int index)方法，根据指定的子栈，执行 pop 操作。

设想当弹出栈1 的栈顶元素时，我们需要移出栈2 的栈底元素，并将其推到栈1中。随后，将栈3的栈底元素推入栈2，将栈4的栈底元素推入栈3，以此类推。

有人可能会说，没必要执行“推入”操作，有些栈不填满也可以啊！而且还降低了时间复杂度。但是若之后有人假定所有的栈（最后一个栈除外）都是填满的，就可能出现意想不到的 error！这个问题并没有“标准答案”，你应该跟面试官讨论各种做法的优劣。

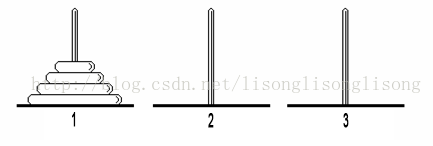
3.4 在经典问题汉诺塔中，有3根柱子及N个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自底向上从大到小依次套在第一根柱子上（即每一个盘子只能放在更大的盘子上面）。移动圆盘时有以下限制：

每次只能移动一个盘子
盘子只能从柱子顶端滑出移到下一根柱子
盘子只能叠在比它大的盘子上

请运用栈，编写程序将所有盘子从第一根柱子移到最后一根柱子。

首先我们从最简单的开始整理自己的思路：

当n=1时，因为只有一个盘子，所以可以直接将盘子1从柱1移至柱3.
当n=2时，可以这样将所有盘子从柱1移至柱3：
1. 将盘子1从柱1移至柱2。
2. 将盘子2从柱1移至柱3。
3. 将盘子1从柱2移至柱3。
当n=3时，可以这样将所有盘子从柱1移至柱3：
1. 将上面两个盘子从柱1移至柱2，同上。
2. 将盘子3移至柱3。
3. 将盘子1、2从柱2移至柱3。
当n=4时，可以这样将所有盘子从柱1移至柱3：
1. 将盘子1、2、3移至柱2，具体做法参见前面。
2. 将盘子4移至柱3。
3. 将盘子1、2、3移至柱3。

把柱1上的盘子移至柱3，需要柱2作为缓冲。可以看出，上面的过程是递归的，很自然地就可以导出递归算法。

class Tower
{
private:
    stack<int> disks;  // 用整数的大小表示盘子的大小
public:
    void add(int d);             // 向柱子上添加盘子
    void moveButtomTo(Tower &t); // 移动最下面那块盘子
    void moveDisks(int n, Tower &dest, Tower &buf);  // 利用buf将n块盘子移至dest
};

/*******************实现*********************/
void Tower::add(int d)
{
    if(!disks.empty() && disks.top() <= d) {
        cout << "Error placing disk " << d;
    }
    else {
        disks.push(d);
    }
}

void Tower::moveButtomTo(Tower &t)
{
    int top = disks.top();
    disks.pop();
    t.add(top);
}

// 递归实现 —— 注意使用引用
void Tower::moveDisks(int n, Tower &dest, Tower &buf)
{
    if(n>0) 
    {
        /*将上面的n-1块盘子移至缓冲区*/
        moveDisks(n-1, buf, dest);
        /*将最下面那块盘子移至目的地*/
        moveButtomTo(dest);
        /*将缓冲区的n-1块盘子移至目的地*/
        buf.moveDisks(n-1, dest, *this);
    }
}

/*******************测试*********************/
int main()
{
    Tower tower[3];  // 3根柱子
    for(int i=5; i>0; --i)
        tower[0].add(i);
    // 移动
    tower[0].moveDisks(5, tower[2], tower[1]);

    return 0;
}

3.5 实现一个MyQueue类，该类用两个栈来实现一个队列。

队列和栈的主要区别就是元素进出顺序。假设两个栈分别是 Newest 和 Oldest，为了用这两个栈达到先进先出（FIFO）的效果，在入队时我们将元素压入 Newest 栈，然后将 Newest 的元素弹出，压入 Oldest 栈中（这样就达到了反转的效果），在出队时，我们从 Oldest 栈中弹出元素。

注意，为了避免频繁的执行从 Newest 到 Oldest 的反转操作，我们规定：只有在发现 Oldest 为空时，才执行反转操作 —— 将 Newest 中的所有元素弹出并压入 Oldest 中。

class MyQueue
{
private:
    stack<int> Newest;  // 新入队的元素
    stack<int> Oldest;  // 准备出队的元素
    void reverseStacks();  // 将Newest元素弹出，压入Oldest 
public:
    int size();           // 队列大小
    void enqueue(int v);  // 入队
    int dequeue();        // 出队
    int top();            // 队首元素
};


// Oldest为空才进行反转，避免频繁操作
void MyQueue::reverseStacks()
{
    if(Oldest.empty())  
    {
        while(!Newest.empty()) {
            Oldest.push(Newest.top());
            Newest.pop();
        }
    }
}

int MyQueue::size()
{
    return Oldest.size()+Newest.size();
}

// 压入Newest，最新元素始终位于它的顶端
void MyQueue::enqueue(int v)
{
    Newest.push(v);
}

// 从Oldest出队
int MyQueue::dequeue()
{
    reverseStacks();
    int value = Oldest.top();
    Oldest.pop();
    return value;
}

int MyQueue::top()
{
    reverseStacks();
    return Oldest.top();
}

3.6 编写程序，按升序对栈进行排序（即最大元素位于栈顶）。最多只能使用一个额外的栈存放临时数据，但不得将元素复制到别的数据结构中（如数组）。该栈支持如下操作：push、pop、peek和isEmpty。

可以想到的一种做法是，搜索整个栈，找出最小元素，将其压入另一个栈；然后，在剩余元素中找出最小的，并将其入栈。但这种做法实际上需要两个额外的栈，一个用来存放最终的有序序列，一个在搜索时用作缓冲区。

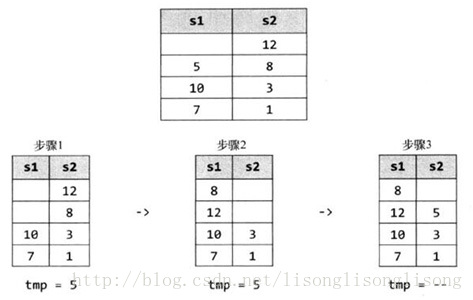
那么，只使用一个额外的栈怎么做呢？可以从S1逐一弹出元素，然后按顺序插入S2中，如下图所示：

S1是未排序的，S2是排好序的：

从S1中弹出5，我们需要在S2中找到合适的位置插入这个数，所以将 12 和 8 移至 S1 中，然后将 5 压入 S2。
那么 8 和 12 需不需要移回 S2 呢？其实不需要，对于这两个数，我们可以像处理 5 那样重复相关步骤就可以了。

stack<int> Sort(stack<int> s)
{
    stack<int> r;
    while(!s.empty())
    {
        int tmp = s.top();
        s.pop();          // 弹出元素存到临时变量
        while(!r.empty() && r.top() > tmp)
        {
            s.push(r.top());
            r.pop();
        }
        r.push(tmp);
    }
    return r;
}

3.7 有家动物收容所只收容狗与猫，且严格遵守“先进先出”的原则。在收养该收容所的动物时，收养人只能收养所有动物中“最老”（根据进入收容所的时间长短）的动物，或者，可以挑选猫或狗（同时必须收养此类动物中“最老”的）。换言之，收养人不能自由挑选想收养的对象。请创建适用于这个系统的数据结构，实现各种操作方法，比如 enqueue、dequeueAny、dequeueDog 和 dequeueCat 等。

思路一：只维护一个队列。那么 dequeueAny 就容易实现，而 dequeueDog 和 dequeueCat 就需迭代访问整个队列，找到第一只被收养的狗或猫。这种解法明显效率不高。

思路二：为猫和狗各维护一个队列。那么 dequeueDog 和 dequeueCat 很容易实现，而 dequeueAny 需要比较猫队列与狗队列的队首，看哪个“更老”。为了方便 dequeueAny 的实现，我们给每个动物加一个额外的变量，以标记进入队列的先后顺序。这种解法显然更简单更高效！

class Animal
{
public:
    string name;
    int order;    // 标记先后顺序
    Animal(string s):name(s){}
};
/******* 狗 *******/
class Dog : public Animal
{
public:
    Dog(string s):Animal(s){}
};

/******* 猫 *******/
class Cat : public Animal
{
public:
    Cat(string s):Animal(s){}
};

/*******队列*******/
class Queue
{
private:
    list<Dog> dogs;
    list<Cat> cats;
    int order;
public:
    Queue():order(0){}
    void enqueue(Dog d)
    {
        d.order = order++;
        dogs.push_back(d);
    }
    void enqueue(Cat c)  // 重载
    {
        c.order = order++;
        cats.push_back(c);
    }
    Dog dequeueDog()
    {
        Dog d = dogs.front();
        dogs.pop_front();
        return d;
    }
    Cat dequeueCat()
    {
        Cat c = cats.front();
        cats.pop_front();
        return c;
    }
    Animal dequeueAny()
    {
        if(dogs.size() == 0)
            return dequeueCat();
        if(cats.size() == 0)
            return dequeueDog();

        if(dogs.front().order < cats.front().order)
            return dequeueDog();
        else
            return dequeueCat();
    }
};

下面的题是关于树或图，做下面的题之前，首先我们要能够创建一棵二叉树或一个图：

创建二叉树：二叉树是什么相信就不用我多说了，可以递归地根据输入创建一棵二叉树。

typedef struct TreeNode
{
    int data;
    TreeNode* left;
    TreeNode* right;
} *BiTree;

// 递归地创建二叉树
void createBinaryTree(BiTree &T)
{
    int x;
    cin >> x;
    if(x < 0) {
        T = NULL;
        return;
    }
    T = (TreeNode*)malloc(sizeof(TreeNode));
    T->data = x;
    createBinaryTree(T->left);
    createBinaryTree(T->right);
}

int main()
{
    BiTree T;
    createBinaryTree(T); 
    getchar();
    return 0;
}

创建二叉查找树：可以由一个数组生成一棵二叉查找树，见《二叉查找树（BST）》。
创建图：图有两种存储方式，邻接矩阵和邻接表，这里采用邻接表来创建图。

class Graph  
{
public: 
    int V;                         // 顶点数  
    list<int> *adj;                // 邻接表  

    Graph(int V);                  // 构造函数  
    void addEdge(int v, int w);    // 向图中添加边   
};  

/* 构造函数 */  
Graph::Graph(int V)  
{  
    this->V = V;  
    adj = new list<int>[V];  
}

/* 添加边，构造邻接表 */  
void Graph::addEdge(int v, int w)  
{  
    adj[v].push_back(w);          // 将w添加到v的链表  
}

4.1 实现一个函数，检查二叉树是否平衡。在这个问题中，平衡树的定义如下：任意一个结点，其两棵子树的高度差不超过1。

本题明确地给出了平衡树的定义，我们的解法就是根据定义直接递归检查每棵子树的高度。代码中的 checkHeight 方法以递归方式获取左右子树的高度。若子树是平衡的，返回该子树的实际高度；若子树不平衡，返回-1，这时所有递归都会立即返回：

/* 
 * 平衡返回高度，不平衡返回-1
 */
int checkHeight(BiTree T)
{
    if(T == NULL)
        return 0;

    /* 检查左子树是否平衡 */
    int leftHeight = checkHeight(T->left);
    if(leftHeight == -1)
        return -1;  

    /* 检查右子树是否平衡 */
    int rightHeight = checkHeight(T->right);
    if(rightHeight == -1)
        return -1;

    /* 检查当前结点是否平衡 */
    int diff = leftHeight>rightHeight ? 
        leftHeight-rightHeight : rightHeight-leftHeight;
    if(diff > 1)  // 不平衡，返回-1
        return -1;
    else          // 平衡，返回高度
        return leftHeight>rightHeight ? leftHeight+1 : rightHeight+1;
}


bool isBalance(BiTree T)
{
    if(checkHeight(T) == -1)
        return false;
    else
        return true;
}

4.2 给定有向图，设计一个算法，找出两个结点之间是否存在一条路径。

只需通过图的遍历，比如深度优先搜索或广度优先搜索，就能解决这个问题。

我们从其中一个结点出发，在遍历过程中检查是否找到另一个结点。在这个算法中，访问过的结点都应标记为“已访问”，以免循环和重复访问结点。下面的示例代码使用了广度优先搜索：

bool isPathExist(Graph g, int start, int end)
{
    list<int> queue;  // 当做队列

    int V = g.getVertexNum();  // 顶点个数
    bool *visited = new bool[V];  
    for(int i=0; i<V; ++i)  
        visited[i] = false; 

    visited[start] = true; // 将当前顶点标记为已访问并压入队列
    queue.push_back(start);

    list<int>::iterator i;
    int node;
    while(!queue.empty())
    {
        node = queue.front(); // 出队
        queue.pop_front();

        for(i=g.adj[node].begin(); i!=g.adj[node].end(); ++i)
        {
            if(!visited[*i])
            {
                if(*i == end)  // 是否等于另一个结点
                    return true;
                else
                {
                    visited[*i] = true;
                    queue.push_back(*i);
                }
            }
        }
    }
    return false;
}

4.3 给定一个有序整数数组，元素各不相同且按升序排列，编写一个算法，创建一棵高度最小的二叉查找树。

要让二叉查找树的高度最小，就必须让左右子树的结点数越接近越好。根据二叉查找树的性质（中序遍历的序列是一个递增的有序序列），可以让该数组中间的值成为根节点，前半区间成为左子树，后半区间成为右子树。然后，每一个区间中间的值又成为子树的根节点，以此类推。

TreeNode* createMinBST(int A[], int low, int high)
{
    if(low > high)   /*递归终止条件*/
        return NULL; 

    int mid = (low + high)/2;
    TreeNode* T = (TreeNode*)malloc(sizeof(TreeNode));
    T->data = A[mid];
    T->left = createMinBST(A, low, mid-1);
    T->right = createMinBST(A, mid+1, high);
    return T;
}

4.4 给定一棵二叉树，设计一个算法，创建含有某一深度上所有结点的链表（比如，若一棵树的深度为D，则会创建出D个链表）。

根据题意，你可能认为这个问题需要一层一层遍历，每一层构成一个链表。但其实可以用任意方式遍历树，只要记住结点位于哪一层即可。

下面是使用先序遍历实现的一个例子：

void createLevelLists(BiTree T, vector<list<TreeNode*>> &lists, int level)
{
    if(T == NULL)   /*递归终止条件*/
        return;

    if(lists.size() <= level)
    {
        list<TreeNode*> lst;
        lst.push_back(T);
        lists.push_back(lst);
    }
    else
    {
        lists.at(level).push_back(T);
    }

    createLevelLists(T->left, lists, level+1);  // 左子树
    createLevelLists(T->right, lists, level+1); // 右子树
}

当然，你也可以使用其他遍历方式，比如层序遍历、广度优先搜索。

4.5 实现一个函数，检查一棵二叉树是否为二叉查找树。

思路一：检查中序序列是否是升序。这是二叉查找树的性质，但需要注意的是，这种方法无法正确处理树中的重复值。若假定这棵树不包含重复值，则这种方法是有效的。

bool inOrder(BiTree T, int &last)
{
    if(T == NULL)  /*递归终止条件*/ 
        return true;

    /*检查左子树*/
    if(!inOrder(T->left, last))
        return false;

    /*检查当前结点*/
    if(T->data <= last)
        return false;
    last = T->data;

    /*检查右子树*/
    if(!inOrder(T->right, last))
        return false;

    return true;
}

bool checkBST(BiTree T)
{
    int last = INT_MIN;
    return inOrder(T, last);
}

思路二：自上而下传递最小和最大值，判断每个结点是否在范围内。假定根结点的值是20，最开始的范围是（INT_MIN,INT_MAX），根结点明显在这个范围内。然后判断左孩子是否在（INT_MIN, 20）这个范围内，右孩子是否在（20 ,INT_MAX）这个范围内。以此类推，递归下去。

bool checkBST(BiTree T, int min, int max)
{
    if(T == NULL)  /*递归终止条件*/ 
        return true;

    if(T->data <= min || T->data > max)
        return false;

    if(!checkBST(T->left,min,T->data) || !checkBST(T->right,T->data,max))
        return false;

    return true;
}

bool checkBST(BiTree T)
{
    return checkBST(T, INT_MIN, INT_MAX);
}

4.6 设计一个算法，找出二叉查找树中指定结点的“下一个”结点（即中序后继）。可以假定每个结点都含有指向父结点的连接。

见《BST的前驱与后继》，本题要求的是中序遍历中的后继结点。求一个结点 x 的后继，有两种情况：

若结点 x 的右子树不为空，则 x 的后继是右子树中值最小的结点，即右子树最左边的结点。
若结点 x 的右子树为空，表示已遍访 x 的子树。我们必须回到 x 的父结点，记父结点为 p ：
- 如果 x 是 p 的左儿子，那么下一个要访问的结点就是 p ；
- 如果 x 是 p 的右儿子，表示已遍访 p 的子树，这时需从 p 往上继续访问，直到遇到一个祖先结点 pp，它的左儿子也是结点 x 的祖先。

TreeNode* successor_BST(TreeNode* n)
{
    if(n == NULL)
        return NULL;

    if(n->right != NULL)
    {
        TreeNode* tmp = n->right;
        while(tmp->left!=NULL)
        {
            tmp = tmp->left;
        }
        return tmp;
    }
    else
    {
        TreeNode* p = n->parent;
        while(p!=NULL && p->right==n)
        {
            n = p;
            p = p->parent;
        }
        return p;
    }
}

4.7 设计并实现一个算法，找出二叉树中某两个结点的第一个共同祖先。不得将额外的结点储存在另外的数据结构中。注意：这不一定是二叉查找树。

我们在解题之前应该先要问问面试官，这棵树的结点是否包含指向父结点的指针。

情况一：如果每个结点中包含指向父结点的指针，那么就可以直接向上追踪 p 和 q 的路径，直到两者相交。当然，在向上追踪的过程中我们需要标记结点是否已经被访问过，比如可以给结点添加isVisited域、或者将已访问结点映射到散列表。
情况二：如果结点不包含指向父结点的指针，又不得将额外的结点储存在另外的数据结构中。那么我们的做法就是：从上向下判断，若 p 和 q 都在某结点的左边，就到左子树中查找共同祖先；若都在该结点的右边，则在右子树中查找共同祖先。要是 p 和 q 不在同一边，那么就表示已经找到第一个共同祖先了。

// 若p为root的子孙，则返回true
bool cover(TreeNode* root, TreeNode* p)
{
    if(root == NULL)
        return false;
    if(root == p)
        return true;
    return cover(root->left, p) || cover(root->right, p);
}

TreeNode* getCommonAncester(BiTree T, TreeNode* p, TreeNode* q)
{
    if(T == NULL)
        return NULL;
    if(T == p || T == q)
        return T;

    bool pAtLeft = cover(T->left, p);
    bool qAtLeft = cover(T->left, q);

    /*若p和q不在同一边，则表示已经找到第一个共同祖先*/
    if(pAtLeft != qAtLeft)
        return T;
    /*若在同一边，遍访那一边*/
    TreeNode* child = pAtLeft ? T->left : T->right;
    return getCommonAncester(child, p, q);
}

TreeNode* commonAncester(BiTree T, TreeNode* p, TreeNode* q)
{
    if(!cover(T, p) || !cover(T, q))  // --错误检查--
        return NULL;

    return getCommonAncester(T, p, q);
}

4.8 你有两棵非常大的二叉树：T1，有几百万个结点；T2，有几百个结点。设计一个算法，判断T2是否为T1的子树。（如果T1有这么一个结点n，其子树与T2一模一样，则T2为T1的子树。也就是说，从结点n处把树砍断，得到的树与T2完全相同。）

首先考虑小数据量的情况，可以求出两棵树的前序和中序遍历序列，若 T2 前序遍历是 T1 前序遍历的子串，并且 T2 中序遍历是 T1 中序遍历的子串，则 T2 为 T1 的子树。假设T1的节点数为 N，T2的节点数为 M。遍历两棵树的时间复杂度是 O(N + M)，判断字符串是否为另一个字符串的子串的复杂性也是 O(N + M)（比如使用KMP算法）。所以总的时间复杂度是O(N+M)，所需的空间也是O(N+M)。———— 这里需要注意一点：对于左结点或者右结点为 null 的情况，需要在字符串中插入特殊字符表示。

对于简单的情形，上面的解法还算不错。但是当数据量非常大时，暂存前序和中序序列可能要占用太多的内存，所以我们考虑另一种解法：遍历 T1，每当 T1 的某个节点与 T2 的根节点值相同时，就判断两棵子树是否相同。假设 T2 的根节点在 T1 中出现了 k 次，那么算法的时间复杂度就是O(N + k*M)，最坏情况下是O(N*M)。

// 匹配两棵子树，完全一样返回true
bool matchTree(TreeNode* t1, TreeNode* t2)
{
    if(t1 == NULL && t2 == NULL) /*若两者都为空*/
        return true;
    if(t1 == NULL || t2 == NULL) /*若只有一个为空*/
        return false;

    if(t1->data != t2->data)
        return false;

    return matchTree(t1->left,t2->left) && matchTree(t1->right,t2->right);
}

// 遍历大树t1，当某个结点与t2根结点相同，matchTree判断
bool subTree(BiTree t1, BiTree t2)
{
    if(t1 == NULL)
        return false;  /*大的树已经空了，还未找到子树*/
    if(t1->data == t2->data)
    {
        if(matchTree(t1, t2))
            return true;
    }
    return subTree(t1->left, t2) || subTree(t1->right, t2);
}

bool containTree(BiTree t1, BiTree t2)
{
    if(t2 == NULL)  /*空树一定是子树*/
        return true; 
    return subTree(t1, t2);
}

对于上面的两种解法，哪种解法比较好呢？

方法一会占用 O(N + M) 的内存，而另外一种解法只会占用 O(logN + logM) 的内存（递归的栈内存）。当考虑扩展性时，内存使用的多寡是个很重要的因素。
方法一的时间复杂度为O(N + M)，方法二最差的时间复杂度是O(N*M)。但是最差情况的时间复杂度并没有代表性，我们需要进一步观察，因为更可能的情况是很早就发现两棵树的不同，早早的退出了 matchTree。

总的来说，在空间效率上，第二种解法更好。在时间上，需要通过实际数据来验证。

4.9 给定一棵二叉树，其中每个结点都含有一个数值。设计一个算法，打印结点数值总和等于某个给定值的所有路径。注意，路径不一定非得从二叉树的根结点或叶结点开始或结束。

下面我们采用简化推广法来解题。

Step 1 ：简化——假设路径必须从根节点开始，但可以在任意结点结束，该怎么解决？

在这种情况下，问题就会变得容易很多。我们可以从根节点开始，向下访问子节点，计算每条路径上到当前节点为止的数值总和，若与给定值相同则打印当前路径。注意，就算找到总和，仍要继续访问这条路径（因为可能存在正负相抵消的情况）。

Step 2 ：推广——路径可从任意结点开始

如果路径可以从任意结点开始，在任意结点结束。在这种情况下我们稍作调整，对于每个结点，都向“上”检查是否有总和为 sum 的路径。具体来讲就是：递归访问每个结点 p 时，我们将 root 到 p 的完整 path 传入函数；然后，函数会从 p 到 root 逆序将结点上的值加起来，当每条子路径的总和等于 sum 时，打印该条子路径。

代码如下：

// 打印从start到end的路径
void print(int path[], int start, int end)
{
    for(int i=start; i<=end; ++i)
        cout << path[i] << " ";
    cout << endl;
}

// 求一棵子树的高度
int depth(TreeNode* n)
{
    if(n == NULL)
        return 0;
    else
    {
        int leftDepth = depth(n->left);
        int rightDepth = depth(n->right);
        return leftDepth>rightDepth ? leftDepth+1 : rightDepth+1;
    }
}

void findSum(BiTree T, int sum, int path[], int level)
{
    if(T == NULL)
        return;
    /*将当前结点插入路径*/
    path[level] = T->data;

    /*从当前结点到root结点，看是否存在和为sum的路径*/
    int t = 0;
    for(int i=level; i>=0; --i)
    {
        t += path[i];
        if(t == sum)
            print(path, i, level);
    }
    /*递归*/
    findSum(T->left, sum, path, level+1);
    findSum(T->right, sum, path, level+1);
}

void findSum(BiTree T, int sum)
{
    int dep = depth(T);
    int *path = (int*)malloc(dep*sizeof(int));
    findSum(T, sum, path, 0);

    free(path);/*释放内存*/
}