径向基（RBF）神经网络

径向基（RBF）神经网络

2015-06-02 16:51  4033人阅读  评论(0)  收藏  举报

RBF网络能够逼近任意非线性的函数。可以处理系统内难以解析的规律性，具有很好的泛化能力，并且具有较快的学

习速度。当网络的一个或多个可调参数（权值或阈值）对任何一个输出都有影响时，这样的网络称为全局逼近网络。

由于对于每次输入，网络上的每一个权值都要调整，从而导致全局逼近网络的学习速度很慢，比如BP网络。如果对于

输入空间的某个局部区域只有少数几个连接权值影响输出，则该网络称为局部逼近网络，比如RBF网络。接下来重点

先介绍RBF网络的原理，然后给出其实现。先看如下图

   

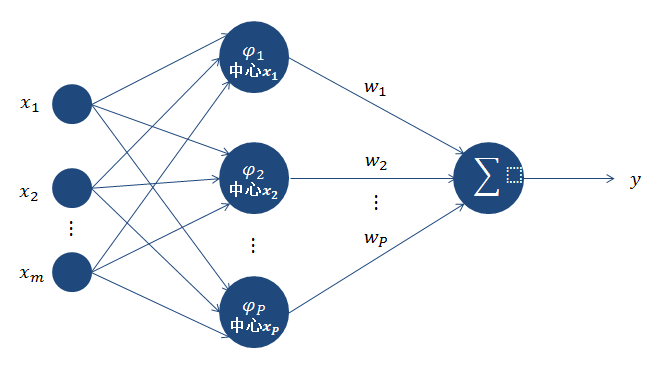
 正则化的RBF网络参考这里。下面是网上找的一个比较好的Python的RBF网络实现。

代码：

[python]  view plain  copy

1. from scipy import *  
2. from scipy.linalg import norm, pinv  
3.    
4. from matplotlib import pyplot as plt  
5.    
6. class RBF:  
7.        
8.     def __init__(self, indim, numCenters, outdim):  
9.         self.indim = indim  
10.         self.outdim = outdim  
11.         self.numCenters = numCenters  
12.         self.centers = [random.uniform(-1, 1, indim) for i in xrange(numCenters)]  
13.         self.beta = 8  
14.         self.W = random.random((self.numCenters, self.outdim))  
15.            
16.     def _basisfunc(self, c, d):  
17.         assert len(d) == self.indim  
18.         return exp(-self.beta * norm(c-d)**2)  
19.        
20.     def _calcAct(self, X):  
21.         # calculate activations of RBFs  
22.         G = zeros((X.shape[0], self.numCenters), float)  
23.         for ci, c in enumerate(self.centers):  
24.             for xi, x in enumerate(X):  
25.                 G[xi,ci] = self._basisfunc(c, x)  
26.         return G  
27.        
28.     def train(self, X, Y):  
29.         """ X: matrix of dimensions n x indim  
30.             y: column vector of dimension n x 1 """  
31.            
32.         # choose random center vectors from training set  
33.         rnd_idx = random.permutation(X.shape[0])[:self.numCenters]  
34.         self.centers = [X[i,:] for i in rnd_idx]  
35.            
36.         print "center", self.centers  
37.         # calculate activations of RBFs  
38.         G = self._calcAct(X)  
39.         print G  
40.            
41.         # calculate output weights (pseudoinverse)  
42.         self.W = dot(pinv(G), Y)  
43.            
44.     def test(self, X):  
45.         """ X: matrix of dimensions n x indim """  
46.            
47.         G = self._calcAct(X)  
48.         Y = dot(G, self.W)  
49.         return Y  
50.    
51.         
52. if __name__ == '__main__':  
53.     n = 100  
54.     x = mgrid[-1:1:complex(0,n)].reshape(n, 1)  
55.     # set y and add random noise  
56.     y = sin(3*(x+0.5)**3 - 1)  
57.     # y += random.normal(0, 0.1, y.shape)  
58.        
59.     # rbf regression  
60.     rbf = RBF(1, 10, 1)  
61.     rbf.train(x, y)  
62.     z = rbf.test(x)  
63.          
64.     # plot original data  
65.     plt.figure(figsize=(12, 8))  
66.     plt.plot(x, y, 'k-')  
67.        
68.     # plot learned model  
69.     plt.plot(x, z, 'r-', linewidth=2)  
70.        
71.     # plot rbfs  
72.     plt.plot(rbf.centers, zeros(rbf.numCenters), 'gs')  
73.        
74.     for c in rbf.centers:  
75.         # RF prediction lines  
76.         cx = arange(c-0.7, c+0.7, 0.01)  
77.         cy = [rbf._basisfunc(array([cx_]), array([c])) for cx_ in cx]  
78.         plt.plot(cx, cy, '-', color='gray', linewidth=0.2)  
79.        
80.     plt.xlim(-1.2, 1.2)  
81.     plt.show()  
82.       

最后提供Github上的一个C++实现的RBF，供日后参考。