Java优先级队列(堆)及对象的比较

---

一、二叉树的顺序存储

1.1 存储方式

使用数组保存二叉树结构，方式即将二叉树用层序遍历方式放入数组中。
一般只适合表示完全二叉树，因为非完全二叉树会有空间的浪费。这种方式的主要用法就是堆的表示。

---

1.2 下标关系

• 已知双亲(parent)的下标，则：
  左孩子(left)下标 = 2 * parent + 1;
  右孩子(right)下标 = 2 * parent + 2;
• 已知孩子（不区分左右）(child)下标，则：
  双亲(parent)下标 = (child - 1) / 2;

二、堆（Heap）

2.1 堆的相关概念

1. 堆逻辑上是一棵完全二叉树；
2. 堆物理上是保存在数组中；
3. 满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆；
4. 反之，则是小堆，或者小根堆，或者最小堆；
5. 堆的基本作用是：快速找集合中的最值。

---

2.2 操作-向下调整

前提：左右子树必须已经是一个堆，才能调整。

创建一个大根堆

建堆是自底向上的建堆方式。
以大根堆为例，首先得创建一个大根堆：

public class TestHeap {
   
    public int[] elem;
    public int usedSize;
    public TestHeap(){
   
        this.elem = new int[10];
    }

    /**
     * 创建大根堆
     * @param array
     */
    public  void  creatHeap(int[] array){
   

        for (int i = 0; i < array.length; i++) {
   
            this.elem[i] = array[i];
            usedSize++;
        }

        //parent代表每颗子树的根节点 ，(array.length - 1)最后一个节点的下标，(array.length - 1 - 1) / 2最后一个节点的根节点
        for(int parent= (array.length - 1 - 1) / 2; parent >= 0; parent--)
            //第二个参数每次调整的结束位置是不确定的
            adjustDown(parent,this.usedSize);
    }

测试代码：

public static void main(String[] args) {
   
        int[] arr = {
   1,5,3,8,7,6};
        TestHeap testHeap = new TestHeap();
        testHeap.creatHeap(arr);
        //在此处打断点调试
        System.out.println("dvsfb");
    }

输出结果：

// 建堆前
int[] array = {
    1,5,3,8,7,6 };
// 建堆后
int[] array = {
    8,7,6,5,1,3 };

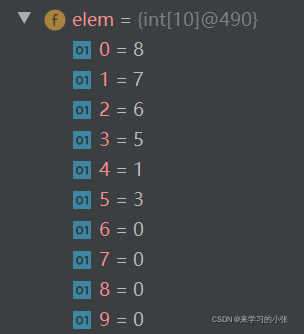
堆排序中建堆过程时间复杂度为O(n)

时间复杂度详解
自底向上的建堆方式，即 Floyd 建堆算法。因为方向相反、自顶向下的建堆方式的时间复杂度为 O(n·logn)。

假设目标堆是一个满堆，即第 k 层节点数为 2ᵏ。输入数组规模为 n, 堆的高度为 h, 那么 n 与 h 之间满足 n = 2ʰ⁺¹ - 1，可化为 h = log₂(n+1) - 1。 (层数 k 和高度 h 均从 0 开始，即只有根节点的堆高度为0，空堆高度为 -1)。建堆过程中每个节点需要一次下滤操作，交换的次数等于该节点到叶节点的深度。那么每一层中所有节点的交换次数为节点个数乘以叶节点到该节点的深度（如第一层的交换次数为 2⁰ · h，第二层的交换次数为 2¹ · (h-1)，如此类推）。从堆顶到最后一层的交换次数 Sn 进行求和：
Sn = 2⁰ · h + 2¹ · (h - 1) + 2² · (h - 2) + ...... + 2ʰ⁻² · 2 + 2ʰ⁻¹ · 1 + 2ʰ · 0；记为①；
①经化简为: Sn = h + 2¹ · (h - 1) + 2² · (h - 2) + ...... + 2ʰ⁻² · 2 + 2ʰ⁻¹；
对①等于号左右两边乘以2，记为②式：
②: 2Sn = 2¹ · h + 2² · (h - 1) + 2³ · (h - 2) + ...... + 2ʰ⁻¹ · 2 + 2ʰ；
用②式减去①式，其中②式的操作数右移一位使指数相同的部分对齐（即错位相减法）：

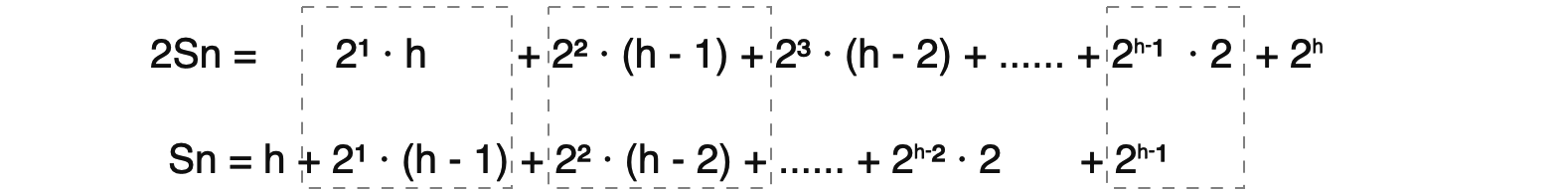
化简可得③式：
③ : Sn = -h + 2¹ + 2² + 2³ + ...... + 2ʰ⁻¹ + 2ʰ；
对指数部分使用等比数列求和公式：

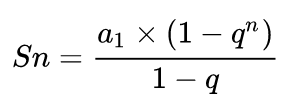
得：

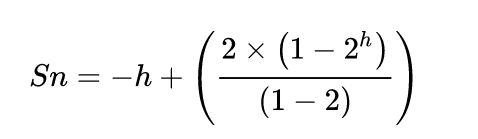
Sn =2ʰ⁺¹ - (h + 2)在上述过程中，已经达到n和h的关系为： h = log₂(n+1) - 1，将其代入Sn中得：Sn =(n+1)(log₂(n+1)-1+2)
化简后为：Sn = n - log₂(n + 1)
而对于对数函数，当n趋近于一定值时，其结果相对于x轴趋于平缓，并且变化幅度不大，因此最终可得渐进复杂度为 O(n)。

向下调整的过程

1. parent 如果已经是叶子结点，则整个调整过程结束。
2. 定义根节点为 parent，则其左孩子节点为：child = 2 * parent+ 1；
3. 找到左右孩子的最大值，前提是的有右孩子， 因为堆的存储结构是数组，所以判断是否有右孩子即判断右孩子下标是否越界，即 child+ 1< len表明未越界，如果有右孩子并且左孩子比右孩子小，则child++；即右孩子为child；
4. 确定 parent 和 child，孩子和父亲的节点大小，如果孩子节点大，则进行交换；
5. 因为 parent位置的堆的性质可能被破坏，所以把 child视作 parent，在parent的基础上重新定义child，向下重复以上过程。

代码示例：

 public void adjustDown(int root,int len){
   
 	int parent = root;
 	int child = 2 * parent+ 1;//左孩子
 	while(child < len){
   
		//找到左右孩子的最大值，前提是的有右孩子
        //如果有右孩子并且左孩子比右孩子小，则child++
 		if(child + 1 < len && elem[child] < elem[child + 1]){
   
 		child++;
 		}
 		//判断孩子和父亲的节点大小，如果孩子节点大，则进行交换
 		if(elem[child] > elem[parent]){
   
 			int tmp = elem[child];
 			elem[child] = elem[parent];
 			 elem[parent] = tmp;
 			 parent = child;
 			 child = 2* parent +1;
 		}else{
   
 		 //当调整过程中，已经没有可以继续再进行调整的节点了，直接break结束
	 		break