定理:F(n)和f(n)是定义在非负整数集合上的两个函数,并且满足条件
F(n)=∑d|nf(d)
,那么我们得到结论
f(n)=∑d|nμ(d)F(n/d)
。
在上面的公式中有一个函数
μ(d)
,它的定义如下:
(1)若d=1,那么
μ(d)=1
.
(2)若d=
p1p2⋯pk
,均为互异素数,那么
μ(d)=(−1)k
.
(3)其它情况下
μ(d)=0
.
对于函数
μ(d)
,它有如下的常见性质:
- 对任意正整数n有
- 对任意正整数n有
其实它还有另一种描述,本题也是用到这种。那就是:
//求1-n的函数值
bool vis[MAX+10];
int mu[MAX+10],prime[MAX+10],cnt;
void mobi(int n){
memset(vis,false,sizeof(vis));
mu[1]=1;
cnt=0;
for(int i=2;i<=n;++i){
if(!vis[i]){
prime[cnt++]=i;
mu[i]=-1;
}
for(int j=0;j<cnt&&i*prime[j]<=n;++j){
vis[i*prime[j]]=1;
if(i%prime[j]) mu[i*prime[j]]=-mu[i];
else{
mu[i*prime[j]]=0;
break;
}
}
}
}
//另一版本
int prime[maxn];
bool check[maxn];
void Mobius(){
memset(check,false,sizeof(check));
prime[0] = 0;
FOR(i,2,maxn){
if(!check[i]){
prime[++prime[0]] = i;
}
FOR(j,1,prime[0]+1){
if(i*prime[j] >= maxn) break;
check[i*prime[j]] = true;
if(i%prime[j] == 0) break;
}
}
}//求某个数对应的函数值。
int mobi(int n){
int m=1;
for(int i=2;i*i<=n;++i)
if(n%i==0){
m*=-1;
int k=0;
do{
k++;
if(k>1){
m=0;
break;
}
n/=i;
}while(n%i==0);
}
if(n>1) m*=-1;
return m;
}相关题目:
- triple
- count_prime
- 51nod1240








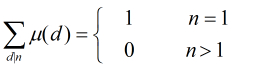
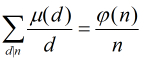
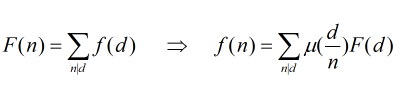














 979
979

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








