线索二叉树（Threaded BinaryTree）

线索二叉树（Threaded BinaryTree）

一、写在前面

   本文主要介绍了中序线索化二叉树及中序线索化二叉树遍历。前序与后序原理相似，但在前、后序线索化二叉树中查找节点的后继较容易，而查找前驱要知道其双亲的信息，前、后序线索化二叉树是不完善的。

   对于n个节点的二叉树，在二叉链存储结构中有n+1个空链域，利用这些空链域存放在某种遍历次序下该节点的前驱节点和后继节点的指针，这些指针称为线索，加上线索的二叉树称为线索二叉树（Threaded BinaryTree）。

二、为什么要线索化？

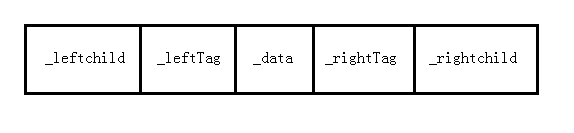
   二叉树的遍历本质上是将一个复杂的非线性结构转换为线性结构，使每个节点都有了唯一前驱和后继（第一个节点无前驱，最后一个节点无后继）。对于二叉树的一个节点，查找其左右子女是方便的，其前驱后继只有在遍历中得到。为了容易找到前驱和后继，有两种方法。一是在节点结构中增加向前和向后的指针，这种方法增加了存储开销，不可取；二是利用二叉树的空链指针。现将前一篇文章的节点结构重新定义如下：

         其中：_leftTag = 1时_leftchild指向左孩子；