问题描述
给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为C。问:应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
形式化描述:给定c >0, wi >0, vi >0 , 1≤i≤n.要求找一n元向量(x1,x2,…,xn,), xi∈{0,1}, ∋ ∑ wi xi≤c,且∑ vi xi达最大.即一个特殊的整数规划问题。
算法设计
首先,要对输入数据进行预处理,将各物品依其单位重量价值从大到小进行排列。在优先队列分支限界法中,节点的优先级由已装袋的物品价值加上剩下的最大单位重量价值的物品装满剩余容量的价值和。
算法首先检查当前扩展结点的左儿子结点的可行性。如果该左儿子结点是可行结点,则将它加入到子集树和活结点优先队列中。当前扩展结点的右儿子结点一定是可行结点,仅当右儿子结点满足上界约束时才将它加入子集树和活结点优先队列。当扩展到叶节点时为问题的最优值。
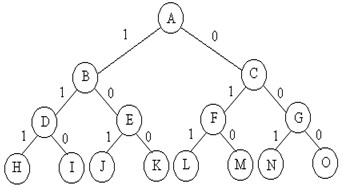
例如:0-1背包问题,当n=3时,w={16,15,15}, p={45,25,25}, c=30。优先队列式分支限界法:处理法则:价值大者优先。{}—>{A}—>{B,C}—>{C,D,E}—>{C,E}—>{C,J,K}—>{C}—>{F,G}—>{G,L,M}—>{G,M}—>{G}—>{N,O}—>{O}—>{}
算法代码实现如下:
1、MaxHeap.h
- template<class T>
- class MaxHeap
- {
- public:
- MaxHeap(int MaxHeapSize = 10);
- ~MaxHeap() {delete [] heap;}
- int Size() const {return CurrentSize;}
- T Max()
- { //查
- if (CurrentSize == 0)
- {
- throw OutOfBounds();
- }
- return heap[1];
- }
- MaxHeap<T>& Insert(const T& x); //增
- MaxHeap<T>& DeleteMax(T& x); //删
- void Initialize(T a[], int size, int ArraySize);
- private:
- int CurrentSize, MaxSize;
- T *heap; // element array
- };
- template<class T>
- MaxHeap<T>::MaxHeap(int MaxHeapSize)
- {// Max heap constructor.
- MaxSize = MaxHeapSize;
- heap = new T[MaxSize+1];
- CurrentSize = 0;
- }
- template<class T>
- MaxHeap<T>& MaxHeap<T>::Insert(const T& x)
- {// Insert x into the max heap.
- if (CurrentSize == MaxSize)
- {
- cout<<"no space!"<<endl;
- return *this;
- }
- // 寻找新元素x的位置
- // i——初始为新叶节点的位置,逐层向上,寻找最终位置
- int i = ++CurrentSize;
- while (i != 1 && x > heap[i/2])
- {
- // i不是根节点,且其值大于父节点的值,需要继续调整
- heap[i] = heap[i/2]; // 父节点下降
- i /= 2; // 继续向上,搜寻正确位置
- }
- heap[i] = x;
- return *this;
- }
- template<class T>
- MaxHeap<T>& MaxHeap<T>::DeleteMax(T& x)
- {// Set x to max element and delete max element from heap.
- // check if heap is empty
- if (CurrentSize == 0)
- {
- cout<<"Empty heap!"<<endl;
- return *this;
- }
- x = heap[1]; // 删除最大元素
- // 重整堆
- T y = heap[CurrentSize--]; // 取最后一个节点,从根开始重整
- // find place for y starting at root
- int i = 1, // current node of heap
- ci = 2; // child of i
- while (ci <= CurrentSize)
- {
- // 使ci指向i的两个孩子中较大者
- if (ci < CurrentSize && heap[ci] < heap[ci+1])
- {
- ci++;
- }
- // y的值大于等于孩子节点吗?
- if (y >= heap[ci])
- {
- break; // 是,i就是y的正确位置,退出
- }
- // 否,需要继续向下,重整堆
- heap[i] = heap[ci]; // 大于父节点的孩子节点上升
- i = ci; // 向下一层,继续搜索正确位置
- ci *= 2;
- }
- heap[i] = y;
- return *this;
- }
- template<class T>
- void MaxHeap<T>::Initialize(T a[], int size,int ArraySize)
- {// Initialize max heap to array a.
- delete [] heap;
- heap = a;
- CurrentSize = size;
- MaxSize = ArraySize;
- // 从最后一个内部节点开始,一直到根,对每个子树进行堆重整
- for (int i = CurrentSize/2; i >= 1; i--)
- {
- T y = heap[i]; // 子树根节点元素
- // find place to put y
- int c = 2*i; // parent of c is target
- // location for y
- while (c <= CurrentSize)
- {
- // heap[c] should be larger sibling
- if (c < CurrentSize && heap[c] < heap[c+1])
- {
- c++;
- }
- // can we put y in heap[c/2]?
- if (y >= heap[c])
- {
- break; // yes
- }
- // no
- heap[c/2] = heap[c]; // move child up
- c *= 2; // move down a level
- }
- heap[c/2] = y;
- }
- }
template<class T>
class MaxHeap
{
public:
MaxHeap(int MaxHeapSize = 10);
~MaxHeap() {delete [] heap;}
int Size() const {return CurrentSize;}
T Max()
{ //查
if (CurrentSize == 0)
{
throw OutOfBounds();
}
return heap[1];
}
MaxHeap<T>& Insert(const T& x); //增
MaxHeap<T>& DeleteMax(T& x); //删
void Initialize(T a[], int size, int ArraySize);
private:
int CurrentSize, MaxSize;
T *heap; // element array
};
template<class T>
MaxHeap<T>::MaxHeap(int MaxHeapSize)
{// Max heap constructor.
MaxSize = MaxHeapSize;
heap = new T[MaxSize+1];
CurrentSize = 0;
}
template<class T>
MaxHeap<T>& MaxHeap<T>::Insert(const T& x)
{// Insert x into the max heap.
if (CurrentSize == MaxSize)
{
cout<<"no space!"<<endl;
return *this;
}
// 寻找新元素x的位置
// i——初始为新叶节点的位置,逐层向上,寻找最终位置
int i = ++CurrentSize;
while (i != 1 && x > heap[i/2])
{
// i不是根节点,且其值大于父节点的值,需要继续调整
heap[i] = heap[i/2]; // 父节点下降
i /= 2; // 继续向上,搜寻正确位置
}
heap[i] = x;
return *this;
}
template<class T>
MaxHeap<T>& MaxHeap<T>::DeleteMax(T& x)
{// Set x to max element and delete max element from heap.
// check if heap is empty
if (CurrentSize == 0)
{
cout<<"Empty heap!"<<endl;
return *this;
}
x = heap[1]; // 删除最大元素
// 重整堆
T y = heap[CurrentSize--]; // 取最后一个节点,从根开始重整
// find place for y starting at root
int i = 1, // current node of heap
ci = 2; // child of i
while (ci <= CurrentSize)
{
// 使ci指向i的两个孩子中较大者
if (ci < CurrentSize && heap[ci] < heap[ci+1])
{
ci++;
}
// y的值大于等于孩子节点吗?
if (y >= heap[ci])
{
break; // 是,i就是y的正确位置,退出
}
// 否,需要继续向下,重整堆
heap[i] = heap[ci]; // 大于父节点的孩子节点上升
i = ci; // 向下一层,继续搜索正确位置
ci *= 2;
}
heap[i] = y;
return *this;
}
template<class T>
void MaxHeap<T>::Initialize(T a[], int size,int ArraySize)
{// Initialize max heap to array a.
delete [] heap;
heap = a;
CurrentSize = size;
MaxSize = ArraySize;
// 从最后一个内部节点开始,一直到根,对每个子树进行堆重整
for (int i = CurrentSize/2; i >= 1; i--)
{
T y = heap[i]; // 子树根节点元素
// find place to put y
int c = 2*i; // parent of c is target
// location for y
while (c <= CurrentSize)
{
// heap[c] should be larger sibling
if (c < CurrentSize && heap[c] < heap[c+1])
{
c++;
}
// can we put y in heap[c/2]?
if (y >= heap[c])
{
break; // yes
}
// no
heap[c/2] = heap[c]; // move child up
c *= 2; // move down a level
}
heap[c/2] = y;
}
}
- //0-1背包问题 分支限界法求解
- #include "stdafx.h"
- #include "MaxHeap.h"
- #include <iostream>
- using namespace std;
- class Object
- {
- template<class Typew,class Typep>
- friend Typep Knapsack(Typep p[],Typew w[],Typew c,int n, int bestx[]);
- public:
- int operator <= (Object a) const
- {
- return d>=a.d;
- }
- private:
- int ID;
- float d;//单位重量价值
- };
- template<class Typew,class Typep> class Knap;
- class bbnode
- {
- friend Knap<int,int>;
- template<class Typew,class Typep>
- friend Typep Knapsack(Typep p[],Typew w[],Typew c,int n, int bestx[]);
- private:
- bbnode * parent; //指向父节点的指针
- bool LChild; //左儿子节点标识
- };
- template<class Typew,class Typep>
- class HeapNode
- {
- friend Knap<Typew,Typep>;
- public:
- operator Typep() const
- {
- return uprofit;
- }
- private:
- Typep uprofit, //节点的价值上界
- profit; //节点所相应的价值
- Typew weight; //节点所相应的重量
- int level; //活节点在子集树中所处的层序号
- bbnode *ptr; //指向活节点在子集中相应节点的指针
- };
- template<class Typew,class Typep>
- class Knap
- {
- template<class Typew,class Typep>
- friend Typep Knapsack(Typep p[],Typew w[],Typew c,int n, int bestx[]);
- public:
- Typep MaxKnapsack();
- private:
- MaxHeap<HeapNode<Typep,Typew>> *H;
- Typep Bound(int i);
- void AddLiveNode(Typep up,Typep cp,Typew cw,bool ch,int lev);
- bbnode *E; //指向扩展节点的指针
- Typew c; //背包容量
- int n; //物品数
- Typew *w; //物品重量数组
- Typep *p; //物品价值数组
- Typew cw; //当前重量
- Typep cp; //当前价值
- int *bestx; //最优解
- };
- template <class Type>
- inline void Swap(Type &a,Type &b);
- template<class Type>
- void BubbleSort(Type a[],int n);
- int main()
- {
- int n = 3;//物品数
- int c = 30;//背包容量
- int p[] = {0,45,25,25};//物品价值 下标从1开始
- int w[] = {0,16,15,15};//物品重量 下标从1开始
- int bestx[4];//最优解
- cout<<"背包容量为:"<<c<<endl;
- cout<<"物品重量和价值分别为:"<<endl;
- for(int i=1; i<=n; i++)
- {
- cout<<"("<<w[i]<<","<<p[i]<<") ";
- }
- cout<<endl;
- cout<<"背包能装下的最大价值为:"<<Knapsack(p,w,c,n,bestx)<<endl;
- cout<<"此背包问题最优解为:"<<endl;
- for(int i=1; i<=n; i++)
- {
- cout<<bestx[i]<<" ";
- }
- cout<<endl;
- return 0;
- }
- template<class Typew,class Typep>
- Typep Knap<Typew,Typep>::Bound(int i)//计算节点所相应价值的上界
- {
- Typew cleft = c-cw; //剩余容量高
- Typep b = cp; //价值上界
- //以物品单位重量价值递减序装填剩余容量
- while(i<=n && w[i]<=cleft)
- {
- cleft -= w[i];
- b += p[i];
- i++;
- }
- //装填剩余容量装满背包
- if(i<=n)
- {
- b += p[i]/w[i]*cleft;
- }
- return b;
- }
- //将一个活节点插入到子集树和优先队列中
- template<class Typew,class Typep>
- void Knap<Typew,Typep>::AddLiveNode(Typep up,Typep cp,Typew cw,bool ch,int lev)
- {
- bbnode *b = new bbnode;
- b->parent = E;
- b->LChild = ch;
- HeapNode<Typep,Typew> N;
- N.uprofit = up;
- N.profit = cp;
- N.weight = cw;
- N.level = lev;
- N.ptr = b;
- H->Insert(N);
- }
- //优先队列式分支限界法,返回最大价值,bestx返回最优解
- template<class Typew,class Typep>
- Typep Knap<Typew,Typep>::MaxKnapsack()
- {
- H = new MaxHeap<HeapNode<Typep,Typew>>(1000);
- //为bestx分配存储空间
- bestx = new int[n+1];
- //初始化
- int i = 1;
- E = 0;
- cw = cp = 0;
- Typep bestp = 0;//当前最优值
- Typep up = Bound(1); //价值上界
- //搜索子集空间树
- while(i!=n+1)
- {
- //检查当前扩展节点的左儿子节点
- Typew wt = cw + w[i];
- if(wt <= c)//左儿子节点为可行节点
- {
- if(cp+p[i]>bestp)
- {
- bestp = cp + p[i];
- }
- AddLiveNode(up,cp+p[i],cw+w[i],true,i+1);
- }
- up = Bound(i+1);
- //检查当前扩展节点的右儿子节点
- if(up>=bestp)//右子树可能含有最优解
- {
- AddLiveNode(up,cp,cw,false,i+1);
- }
- //取下一扩展节点
- HeapNode<Typep,Typew> N;
- H->DeleteMax(N);
- E = N.ptr;
- cw = N.weight;
- cp = N.profit;
- up = N.uprofit;
- i = N.level;
- }
- //构造当前最优解
- for(int j=n; j>0; j--)
- {
- bestx[j] = E->LChild;
- E = E->parent;
- }
- return cp;
- }
- //返回最大价值,bestx返回最优解
- template<class Typew,class Typep>
- Typep Knapsack(Typep p[],Typew w[],Typew c,int n, int bestx[])
- {
- //初始化
- Typew W = 0; //装包物品重量
- Typep P = 0; //装包物品价值
- //定义依单位重量价值排序的物品数组
- Object *Q = new Object[n];
- for(int i=1; i<=n; i++)
- {
- //单位重量价值数组
- Q[i-1].ID = i;
- Q[i-1].d = 1.0*p[i]/w[i];
- P += p[i];
- W += w[i];
- }
- if(W<=c)
- {
- return P;//所有物品装包
- }
- //依单位价值重量排序
- BubbleSort(Q,n);
- //创建类Knap的数据成员
- Knap<Typew,Typep> K;
- K.p = new Typep[n+1];
- K.w = new Typew[n+1];
- for(int i=1; i<=n; i++)
- {
- K.p[i] = p[Q[i-1].ID];
- K.w[i] = w[Q[i-1].ID];
- }
- K.cp = 0;
- K.cw = 0;
- K.c = c;
- K.n = n;
- //调用MaxKnapsack求问题的最优解
- Typep bestp = K.MaxKnapsack();
- for(int j=1; j<=n; j++)
- {
- bestx[Q[j-1].ID] = K.bestx[j];
- }
- delete Q;
- delete []K.w;
- delete []K.p;
- delete []K.bestx;
- return bestp;
- }
- template<class Type>
- void BubbleSort(Type a[],int n)
- {
- //记录一次遍历中是否有元素的交换
- bool exchange;
- for(int i=0; i<n-1;i++)
- {
- exchange = false ;
- for(int j=i+1; j<=n-1; j++)
- {
- if(a[j]<=a[j-1])
- {
- Swap(a[j],a[j-1]);
- exchange = true;
- }
- }
- //如果这次遍历没有元素的交换,那么排序结束
- if(false == exchange)
- {
- break ;
- }
- }
- }
- template <class Type>
- inline void Swap(Type &a,Type &b)
- {
- Type temp = a;
- a = b;
- b = temp;
- }
//0-1背包问题 分支限界法求解
#include "stdafx.h"
#include "MaxHeap.h"
#include <iostream>
using namespace std;
class Object
{
template<class Typew,class Typep>
friend Typep Knapsack(Typep p[],Typew w[],Typew c,int n, int bestx[]);
public:
int operator <= (Object a) const
{
return d>=a.d;
}
private:
int ID;
float d;//单位重量价值
};
template<class Typew,class Typep> class Knap;
class bbnode
{
friend Knap<int,int>;
template<class Typew,class Typep>
friend Typep Knapsack(Typep p[],Typew w[],Typew c,int n, int bestx[]);
private:
bbnode * parent; //指向父节点的指针
bool LChild; //左儿子节点标识
};
template<class Typew,class Typep>
class HeapNode
{
friend Knap<Typew,Typep>;
public:
operator Typep() const
{
return uprofit;
}
private:
Typep uprofit, //节点的价值上界
profit; //节点所相应的价值
Typew weight; //节点所相应的重量
int level; //活节点在子集树中所处的层序号
bbnode *ptr; //指向活节点在子集中相应节点的指针
};
template<class Typew,class Typep>
class Knap
{
template<class Typew,class Typep>
friend Typep Knapsack(Typep p[],Typew w[],Typew c,int n, int bestx[]);
public:
Typep MaxKnapsack();
private:
MaxHeap<HeapNode<Typep,Typew>> *H;
Typep Bound(int i);
void AddLiveNode(Typep up,Typep cp,Typew cw,bool ch,int lev);
bbnode *E; //指向扩展节点的指针
Typew c; //背包容量
int n; //物品数
Typew *w; //物品重量数组
Typep *p; //物品价值数组
Typew cw; //当前重量
Typep cp; //当前价值
int *bestx; //最优解
};
template <class Type>
inline void Swap(Type &a,Type &b);
template<class Type>
void BubbleSort(Type a[],int n);
int main()
{
int n = 3;//物品数
int c = 30;//背包容量
int p[] = {0,45,25,25};//物品价值 下标从1开始
int w[] = {0,16,15,15};//物品重量 下标从1开始
int bestx[4];//最优解
cout<<"背包容量为:"<<c<<endl;
cout<<"物品重量和价值分别为:"<<endl;
for(int i=1; i<=n; i++)
{
cout<<"("<<w[i]<<","<<p[i]<<") ";
}
cout<<endl;
cout<<"背包能装下的最大价值为:"<<Knapsack(p,w,c,n,bestx)<<endl;
cout<<"此背包问题最优解为:"<<endl;
for(int i=1; i<=n; i++)
{
cout<<bestx[i]<<" ";
}
cout<<endl;
return 0;
}
template<class Typew,class Typep>
Typep Knap<Typew,Typep>::Bound(int i)//计算节点所相应价值的上界
{
Typew cleft = c-cw; //剩余容量高
Typep b = cp; //价值上界
//以物品单位重量价值递减序装填剩余容量
while(i<=n && w[i]<=cleft)
{
cleft -= w[i];
b += p[i];
i++;
}
//装填剩余容量装满背包
if(i<=n)
{
b += p[i]/w[i]*cleft;
}
return b;
}
//将一个活节点插入到子集树和优先队列中
template<class Typew,class Typep>
void Knap<Typew,Typep>::AddLiveNode(Typep up,Typep cp,Typew cw,bool ch,int lev)
{
bbnode *b = new bbnode;
b->parent = E;
b->LChild = ch;
HeapNode<Typep,Typew> N;
N.uprofit = up;
N.profit = cp;
N.weight = cw;
N.level = lev;
N.ptr = b;
H->Insert(N);
}
//优先队列式分支限界法,返回最大价值,bestx返回最优解
template<class Typew,class Typep>
Typep Knap<Typew,Typep>::MaxKnapsack()
{
H = new MaxHeap<HeapNode<Typep,Typew>>(1000);
//为bestx分配存储空间
bestx = new int[n+1];
//初始化
int i = 1;
E = 0;
cw = cp = 0;
Typep bestp = 0;//当前最优值
Typep up = Bound(1); //价值上界
//搜索子集空间树
while(i!=n+1)
{
//检查当前扩展节点的左儿子节点
Typew wt = cw + w[i];
if(wt <= c)//左儿子节点为可行节点
{
if(cp+p[i]>bestp)
{
bestp = cp + p[i];
}
AddLiveNode(up,cp+p[i],cw+w[i],true,i+1);
}
up = Bound(i+1);
//检查当前扩展节点的右儿子节点
if(up>=bestp)//右子树可能含有最优解
{
AddLiveNode(up,cp,cw,false,i+1);
}
//取下一扩展节点
HeapNode<Typep,Typew> N;
H->DeleteMax(N);
E = N.ptr;
cw = N.weight;
cp = N.profit;
up = N.uprofit;
i = N.level;
}
//构造当前最优解
for(int j=n; j>0; j--)
{
bestx[j] = E->LChild;
E = E->parent;
}
return cp;
}
//返回最大价值,bestx返回最优解
template<class Typew,class Typep>
Typep Knapsack(Typep p[],Typew w[],Typew c,int n, int bestx[])
{
//初始化
Typew W = 0; //装包物品重量
Typep P = 0; //装包物品价值
//定义依单位重量价值排序的物品数组
Object *Q = new Object[n];
for(int i=1; i<=n; i++)
{
//单位重量价值数组
Q[i-1].ID = i;
Q[i-1].d = 1.0*p[i]/w[i];
P += p[i];
W += w[i];
}
if(W<=c)
{
return P;//所有物品装包
}
//依单位价值重量排序
BubbleSort(Q,n);
//创建类Knap的数据成员
Knap<Typew,Typep> K;
K.p = new Typep[n+1];
K.w = new Typew[n+1];
for(int i=1; i<=n; i++)
{
K.p[i] = p[Q[i-1].ID];
K.w[i] = w[Q[i-1].ID];
}
K.cp = 0;
K.cw = 0;
K.c = c;
K.n = n;
//调用MaxKnapsack求问题的最优解
Typep bestp = K.MaxKnapsack();
for(int j=1; j<=n; j++)
{
bestx[Q[j-1].ID] = K.bestx[j];
}
delete Q;
delete []K.w;
delete []K.p;
delete []K.bestx;
return bestp;
}
template<class Type>
void BubbleSort(Type a[],int n)
{
//记录一次遍历中是否有元素的交换
bool exchange;
for(int i=0; i<n-1;i++)
{
exchange = false ;
for(int j=i+1; j<=n-1; j++)
{
if(a[j]<=a[j-1])
{
Swap(a[j],a[j-1]);
exchange = true;
}
}
//如果这次遍历没有元素的交换,那么排序结束
if(false == exchange)
{
break ;
}
}
}
template <class Type>
inline void Swap(Type &a,Type &b)
{
Type temp = a;
a = b;
b = temp;
}























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








