POJ 2479 Maximum sum （2593）

Description

Given a set of n integers: A={a1, a2,..., an}, we define a function d(A) as below:

Your task is to calculate d(A).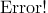

Input

The input consists of T(<=30) test cases. The number of test cases (T) is given in the first line of the input. 
Each test case contains two lines. The first line is an integer n(2<=n<=50000). The second line contains n integers: a1, a2, ..., an. (|ai| <= 10000).There is an empty line after each case.

Output

Print exactly one line for each test case. The line should contain the integer d(A).

Sample Input

1

10
1 -1 2 2 3 -3 4 -4 5 -5

Sample Output

13

题意：给出一段数字，要求出其中两个不交叉的子段的和的最大值。

思路：用DP的方式，从前往后扫一遍求出到每一点的最大和子段的和，然后从后往前扫一遍。

先贴一段好理解的代码，这个代码很好理解但多了几个循环

#include <iostream>
using namespace std;

int Data[50001];//元数据
int x[50001];//从前往后经过每一点的最大sum值
int y[50001];//从后往前经过每一点的最大sum值

int main()
{
	//输入case次数
	int time = 0;
	cin>>time;

	int num = 0;
	int sum = 0;
	//初始化数组
	memset(x, 0, sizeof(x));
	memset(y, 0, sizeof(y));

	while (time--)
	{
		//输入元数据个数
		cin>>num;

		//特例，当元数据只有2个时直接求和
		if (num == 2)
		{
			cin>>Data[0]>>Data[1];
			sum = Data[0] + Data[1];
			cout<<sum<<endl;
			continue;
		}

		//输入元数据并求 从前往后数，到达每一点 并包括该点 的子片段的最大和
		for (int i=0; i<num; i++)
		{
			cin>>Data[i];

			if (i == 0)
			{
				x[i] = Data[i];
			}
			else 
			{
				if (x[i-1] > 0)
				{
					x[i] = x[i-1] + Data[i];
				}
				else
				{
					x[i] = Data[i];
				}
			}
		}

		//从后往前数，到达每一点 并包括该点 的子片段的最大和
		for (int j=(num-1); j>=0; j--)
		{
			if (j == (num - 1))
			{
				y[j] = Data[j];
			}
			else
			{
				if (y[j + 1] > 0)
				{
					y[j] = y[j + 1] + Data[j];
				}
				else
				{
					y[j] = Data[j];
				}
			}
		}

		//无论从前往后还是从后往前，我们都要找到对于起点到该点的最大“子片段”和
		for (int n=1; n<num; n++)
		{
			if (x[n] < x[n-1])
				x[n] = x[n-1];

			if (y[num - n - 1] < y[num - n])
				y[num - n - 1] = y[num - n];
		}

		//我们计算最终对于每一点所能求得的最大和
		for (int k=0; k<(num-1); k++)
		{
			if ((x[k] + y[k+1]) > sum)
				sum = (x[k] + y[k+1]);
		}

		cout<<sum<<endl;
	}
	return 0;
}

上述代码时间上还有优化的地方，特别要注意在for循环中的计算能少则少不然以超过o（n）的复杂度很容易超时

下面这段代码经过改良，值得一提的是用C++流操作时会超时，而用C的scanf则不会。

#include <iostream>
#include <stdio.h>
using namespace std;
#define MIN -0xfffffff


int Data[50001];//元数据
int x[50001];//从前往后经过每一点的最大sum值


int main()
{
	//输入case次数
	int time = 0;
	scanf("%d", &time);
	//cin>>time;


	int num = 0;
	
	//初始化数组


	while (time--)
	{
		//输入元数据个数
		//cin>>num;
		scanf("%d", &num);
		int sum = 0;
		int temp = MIN;
		int out = MIN;


		//输入元数据并求 从前往后数，到达每一点 并包括该点 的子片段的最大和
		for (int i=1; i<=num; i++)
		{
			//cin>>Data[i];
			scanf("%d", &Data[i]);
			sum += Data[i];
			if (sum > temp)
			temp = sum;
			x[i] = temp;
			if (sum < 0)//这一步的判断使得之前超时的部分得以简化，减少了一轮for
				sum = 0;
		}
		temp = MIN;
		sum = 0;
		//从后往前数，到达每一点 并包括该点 的子片段的最大和
		for (int j=num; j>=2; j--)
		{
			sum += Data[j];
			if (sum > temp)
				temp = sum;
			if (x[j - 1] + temp > out)
			{
				out = x[j - 1] + temp;
			}
			if (sum < 0)
				sum = 0;
		}
		printf("%d\n", out);
		//cout<<out<<endl;
	}
	return 0;
}

2593和这个一样，结束的方式不一样而已