椭圆曲线:一个更好的trapdoor构件
椭圆曲线是满足特定数学等式的点的集合。椭圆曲线的方程像如下的样子:
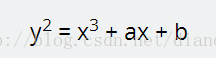
它的图像:
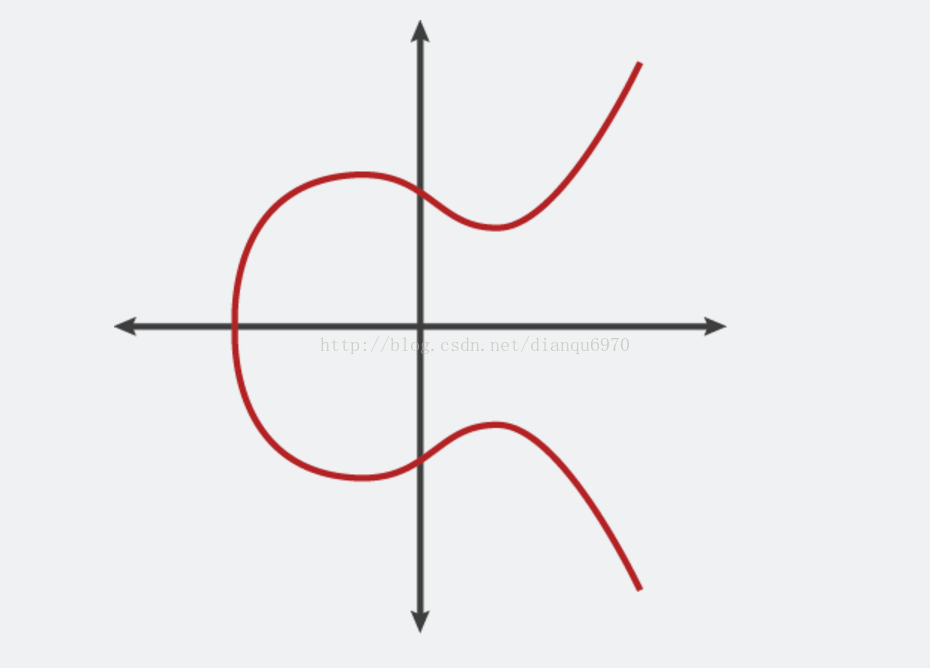
还有其他形式的椭圆曲线的表达形式,但是一般的椭圆曲线方程,一个变量为2阶,一个变量为3阶。它有一些好的属性用于加密。
1. 奇怪的对称性
它是水平对称的。图形是关于x轴对称的。
更有趣的是,任何不垂直的直线最多与曲线有三个交点。
让我们把这个曲线想象成一个奇异的桌球游戏。在曲线上任取两个点,并画一条线进过他们,这个直线将再穿过曲线至多一个点。在这个桌球游戏中,拿一个球从A点射向B点,当它击中曲线时,这个球要么笔直向上弹(在x轴的下面)或者笔直向下弹(在x轴的上方),弹向曲线的另一边。

我们称这个经过两点的桌球叫“打点”。任何两个点通过打点可以得到一个新的点。
A dot B=C
我们可以反复这个规则:
A dot A=B(Adot A,就是取A处的切线)
A dot B=C
A dot C=D
…
这说明了如果你有两个点,经过n次的打点之后将得到一个最终的点。仅仅知道原始点和最终点来找出n是很难的。为了继续拿这个桌球游戏来暗喻,一个人在随机的时间段内按照桌球的规则进行着这个游戏,这是很简单的。但是,如果另一个人在开始后的某段时间进入后,即使他看见了球终止的地方,和球起始的点,他也很难决定打点的次数,除非他全程在看着这个游戏。容易做,却很难解,这个是trapdoor函数的基础。
上述就是基于椭圆加密的一个基本的思想。







 本文介绍了椭圆曲线的概念及其在加密中的应用。椭圆曲线因其独特的性质被广泛应用于现代密码学,尤其是其作为陷阱门函数的基础特性。文章还详细解释了一个基于椭圆曲线的桌球游戏比喻,形象地展示了椭圆曲线加密的基本思想。
本文介绍了椭圆曲线的概念及其在加密中的应用。椭圆曲线因其独特的性质被广泛应用于现代密码学,尤其是其作为陷阱门函数的基础特性。文章还详细解释了一个基于椭圆曲线的桌球游戏比喻,形象地展示了椭圆曲线加密的基本思想。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








