图像增强算法-MSRCR

---

一、Retinex 理论基础

(1)色彩恒常性(Color Constancy):Retinex 理论认为,在不同的光照条件下, 同一个物体的颜色应该是相对稳定的。也就是说,人类的视觉系统能够将物体的 颜色与周围环境的光线相互抵消,从而使得人们感知到的颜色基本上保持不变。
(2)全反射(Full Reflectance):Retinex 理论假设,人类的视觉系统能够分离 物体的表面反射光和阴影部分,从而更好地感知到物体的表面颜色。这意味着, 人们能够将物体的颜色感知与光线的亮度变化相分离。
(3)多尺度比较(Multi-Scale Comparison):Retinex 理论认为,人类的视觉系 统在感知颜色和亮度时,会同时比较多个尺度上的信息。也就是说,人们会比较 物体表面的反射光与周围环境的光在不同尺度上的差异,从而更加准确地感知颜 色和亮度。

观察到的图像 S(x,y) 是光照产生的入射图像 L(x,y) 与物体反射率 R(x,y) 的乘积

S = L × R

对两边取对数

log（R） = log（S）- log（L）

入射图像分量很难直接得到,因此,使用高斯滤波与原始图像进行卷 积操作来代替入射图像分量

log（R） = log（S）- log（S * G）

“ * ” 代表卷积, G 代表高斯滤波

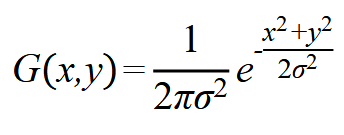
x和y表示距离中心像素的偏差;σ表示高斯核的标准差。当σ值过小时, 滤波器的范围很小,导致平滑效果不够明显,此时图像的原始细节和噪声保留较 多;当σ值过大时,对图像的平滑效果较好,但过度光滑也会导致图像缺乏边缘 细节。

二、多尺度融合（Multi-Scale Retinex, MSR）

单尺度 σ 只能保持某一频段的细节。MSR 把 k 个不同 σi 的G的结果做平均：

log( R ) = (1/k) ∑ ( log( S )- log( S * G ) )

三、色彩恢复（Color Restoration, CR）

MSR 把三个通道独立处理，会导致严重的色偏/灰化。MSRCR 引入颜色恢复因子 C(x,y)：

** R’ = C × R **

Ci表示第i个通道的色彩恢复因子;α和β表示调节参数,α控制颜色修复的强度,β控制颜色修复的影响程度;∑ Ii 表示原始图像的三个通道 在每个像素位置的和

Ci = β × [ log( α × Ii ) – log( Σ Ii ) ]

四、线性映射 & 后处理

线性拉伸到 0~1：

norm = ( R’ – min) / (max – min)

最后在公式中加入一个增益值G和偏移值b得到最终的 MSRCR 算法

Output = G · norm + b

---

代码

import cv2
import numpy as np
import matplotlib.pyplot as plt

# -------------------- 参数区 --------------------
sigmas = (15, 80, 250)    # 高斯核尺度
alpha = 125.0             # 色彩恢复强度
beta  = 46.0              # 增益
G     = 192.0             # 最终增益
b     = -30.0             # 最终偏置
# ----------------------------------------------

def single_scale_retinex(img, sigma):
    """单尺度 Retinex"""
    blurred = cv2.GaussianBlur(img, (0, 0), sigma)
    retinex = np.log10(img + 1e-6) - np.log10(blurred + 1e-6)
    return retinex

def multi_scale_retinex(img, sigmas):
    """多尺度 Retinex 取平均"""
    msr = np.zeros_like(img, dtype=np.float32)
    for s in sigmas:
        msr += single_scale_retinex(img, s)
    return msr / len(sigmas)

def color_restoration(img, msr, alpha, beta):
    """色彩恢复因子 C"""
    img_sum = np.sum(img, axis=2, keepdims=True) + 1e-6
    C = beta * (np.log10(alpha * img + 1) - np.log10(img_sum))
    return C * msr

def msrcr(img_bgr):
    """主函数：MSRCR"""
    img = img_bgr.astype(np.float32) + 1.0  # 避免 log(0)
    msr = multi_scale_retinex(img, sigmas)
    img_cr = color_restoration(img, msr, alpha, beta)
    msrcr_result = G * (img_cr - np.min(img_cr)) / (np.max(img_cr) - np.min(img_cr)) + b
    msrcr_result = np.clip(msrcr_result, 0, 255)
    return msrcr_result.astype(np.uint8)

def simplest_color_balance(img, low_clip=1, high_clip=99):
    """简单的 1%-99% 线性拉伸"""
    out = np.zeros_like(img)
    for ch in range(3):
        a = np.percentile(img[:, :, ch], low_clip)
        b = np.percentile(img[:, :, ch], high_clip)
        channel = np.clip(img[:, :, ch], a, b)
        out[:, :, ch] = 255 * (channel - a) / (b - a + 1e-6)
    return out.astype(np.uint8)

# ------------------ 运行示例 ------------------
if __name__ == '__main__':
    img_path = 'OIP-C.jpg'      # 换成自己的图片
    img_bgr  = cv2.imread(img_path)
    if img_bgr is None:
        raise FileNotFoundError(img_path)

    result = msrcr(img_bgr)
    result = simplest_color_balance(result, low_clip=1, high_clip=99)

    # 可视化
    plt.figure(figsize=(10, 5))
    plt.subplot(1, 2, 1)
    plt.title('Original')
    plt.imshow(cv2.cvtColor(img_bgr, cv2.COLOR_BGR2RGB))
    plt.axis('off')

    plt.subplot(1, 2, 2)
    plt.title('MSRCR')
    plt.imshow(cv2.cvtColor(result, cv2.COLOR_BGR2RGB))
    plt.axis('off')
    plt.tight_layout()
    plt.show()

    # 保存
    cv2.imwrite('msrcr_output.jpg', result)